objetosc

objetosc kurdek: Czworościan foremny o krawędzi a przecięto płaszczyzną równoległa do dwóch skośnych krawędzi i przechodząca w odległości 0,5a od jednej z tych krawędzi. Oblicz objętość brył otrzymanych w wyniku tego przecięcia.

29 maj 22:48

Eta: https://forum.zadania.info/viewtopic.php?t=33326

29 maj 23:01

kurdek: ale tam tylko jest rysunek

29 maj 23:10

kurdek: Ktos to policzy?

29 maj 23:14

kurdek: Czemu tam jest prosrokąt i jak policzyć to?

29 maj 23:19

a7:

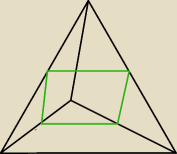
czy ten szkic jest dobry?

29 maj 23:20

a7: https://matematykaszkolna.pl/strona/992.html V_{CZWOROŚCIANU}=a³√2/(12) teraz trzeba wymyślić jak ten prostokąt dzieli ten czworościan

29 maj 23:23

kurdek: Tutaj tez jest to zadanie ale bez rozwiązania https://matematykaszkolna.pl/forum/353268.html Nadal nie rozumiem czemu to prostokąt

29 maj 23:25

kurdek: Skoro to prostokąt to odcina ostrosłup i jaakiś ściety ostrosłup to druga

29 maj 23:26

a7: no dobra to policzmy boki tego (zakładamy, że) prostokąta

29 maj 23:28

mann: Hej a7, pytasz, czy twój szkic jest dobry, jest do kitu

29 maj 23:28

kurdek: Moze nie do kitu ale nie wiem czemu tam jest prostokat

29 maj 23:29

a7:

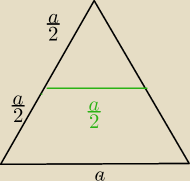
29 maj 23:30

a7: @mann, sorry, ale wiem co myślisz o szkicach najlepszych tutaj rysowników, więc sorry.........

29 maj 23:30

a7: czyli jeden bok tego prostokąta to a/2

29 maj 23:33

a7: czy kąt pod jakim jest krawędź czworościanu do jego podstawy jest równy 60^o

29 maj 23:35

mann:

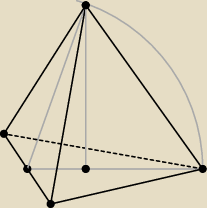
To jest czworościan foremny

29 maj 23:39

a7: @mann a płaszczyzna, która przecina ten czworościan?

29 maj 23:41

a7:

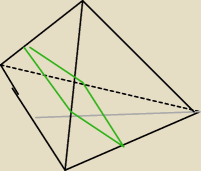
29 maj 23:45

a7: wychodzi na to , że jest to kwadrat o boku a/2, ale mogę się mylić

29 maj 23:46

kurdek: Niech już bedzie ten prostokąt jak policzyc te objetości, wiem ze wystarczy jedną a potem odjąc oc całosci

29 maj 23:46

a7: powstaną dwie bryły trudne do sklasyfikowania dla mnie

29 maj 23:49

a7: myślę, myślę....

29 maj 23:49

a7: ale to jest zadanie z rozszerzenia czy konkursowe?

29 maj 23:53

kurdek: z matury podobno.....

30 maj 00:01

a7: dobra mam, ale nie wiem czy dobrze V₁=2v+v=2*1/3*1/2*a/4*a√3/4*a√3/4+1/3*a/2*a√3/4*a√3/4=3*a³/(64) V₂=V−V₁

30 maj 00:06

a7: rozbiliśmy bryłę mniejszą na trzy bryły, ale zaraz jeszcze nie poprawnie policzone, chwila

30 maj 00:08

a7: V₁=v_{GRANIASTOSŁUPA TRÓJKĄTNEGO}+2*v_{OSTROSŁUPA TRÓJKĄTNEGO "NA BRZEGACH"}

	a√3
V₁=1/2*(		)²sinαh+21/2a√3/4a/4h₂
	4

	a³√2
=		+.......................
	32

trzeba wyliczyć wysokość tych ostrosłupików trójkątnych "bocznych"

30 maj 00:22

a7:

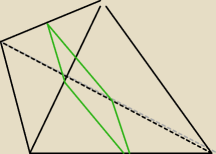
h₂=a√6/6 (?)

	a³√2
czyli wyszło V₁=
	16

	a³√2
V₂=
	48

ale nie wiem czy to jest poprawnie.....

30 maj 00:33

a7: a jeszcze chochlik objętości ostrosłupów nie pomnożone razy 1/3

	a³√2
V₁=
	24

	a³√2
V₂=V₁=
	24

30 maj 00:40

a7:

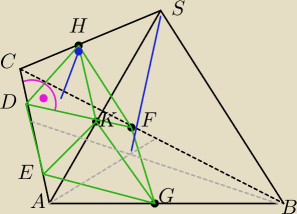
30 maj 00:45

a7: @kurdek czy rozumiesz jak policzyłam, które odcinki?

30 maj 00:46

a7: |DE|=|HK|=a/2 |CD|=|EA|=a/4 |HD|=|KE|=|EG|=|DF|=a√3/4 wysokości ostrosłupików CDFH i EAGK są równe 1/2*H_{CZWOROŚCIANU}=1/2*√6/3=√6/6

	2√2
sinα=sinHDK=sinEKG=H/(1/3*a√3{2})=
	3

30 maj 00:53

kurdek: Musze to przetwaic ale chyba już jutro bo to mnie przersło

30 maj 00:55

a7: w zasadzie możesz trawić od wpisów od godz. 00:22 jeszcze chochlik (kolejny) wysokości ostrosłupików =a√6/6

30 maj 01:08

Eta: Fajne określenie "ostrosłupików " ( podoba mi się)

30 maj 01:10

kurdek: A jak wyszła ostateczna własciwa odpowiedz, spróbuje do niej dojsc

30 maj 01:12

a7: @Eta a wynik dobry?

30 maj 01:37

Mila:

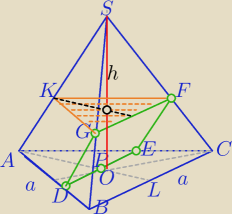
|OS|=H h− wysokość ostrosłupa KGFS

	a√6
H=
	3

ΔADE≡ΔKGF Po dorysowaniu ΔKGF bryła podzielona została na 3 części: 1)Ostrosłup KGFS ∼ostrosłupa ABCS V_ABCS=V 2) graniastosłup ADEKGF 3) wielościan DBGCEF

	\|AP\|
ΔADE∼ΔABC w skali k=		=...?
	\|AL\|

V_KGFS=k³V 4) Vg=P_ΔADE*h_g

Vg

PΔADE*hg

=

VKGFS

1 
*PΔKGF*h
3 

V_g		3h_g
	=
V_KGFS		h

	3h_g
V_g=		*k³V
	h

5)V_w=V−(V_g+V_KGFS)

30 maj 20:24

Eta:

30 maj 22:13

kurdek: A jaki jest ostateczny wynik?

30 maj 23:23

a7:

	\|AP\|		2
k=		=
	\|AL\|		3

	a³√2		2a³√2
V_KGFS=(²₃)³*		=
	12		81

	²₃a*√6		2√6a
h=		=
	3		9

	√6a
h_g=H−h=
	9

	3		2a³√2		a³√2
V_g=V_ADEKGF=		*		=
	2		81		27

	a³√2		a³√2		2a³√2
V_w=V−(V_g+V_KGFS)=		−(		+		)=
	12		27		81

	a³√2		5a³√2
=		−		=
	12		81

	7a³√2
=
	324

31 maj 01:58

a7:

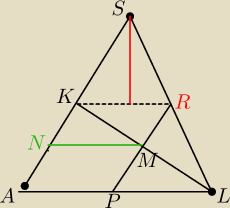
jeszcze raz na podstawię rozwiązania Mili z 20:24 próbuję dokończyć obliczenia

	a√3		a√2		a		a√6
\|AS\|=a \|AL\|=\|SL\|=		\|KL\|=		\|KM\|=		\|NM\|=\|AP\|=\|KR\|=
	2		2		2		4

	AP\|		^a√6₄		√2
k=		=		=
	\|AL\|		^a√3₂		2

	√2		a³√2		a³
V_KGFS=(		)³*		=
	2		12		24

wyliczam h i h_g

	√2
KG=k*a=		a h=U{a√6{3}U√2{2}=U{a√3{3}
	2

	a√6		a{3}		a√3(√2−1)
h_g=H−h=		−		=
	3		3		3

	3h_g		a³(√2−1)
V_g=		*V_KGFS=
	h		24

	a³√2		a³		a³(√2−1)		a³√2
V_w=		−(		+		)=
	12		24		24		24

31 maj 09:04

23: A skąd znamy wartość AP ? pytam bo a7 raz podaje skalę k inna raz inną.

2 cze 21:39

23: Ktoś powie jak policzyć skale k o której pisze Mila ?

2 cze 22:24

a7: 01:58 jest zła skala, gdyż odczytałam ją z rysunku, a 9:34 (31 maj) obliczyłam tę skalę, ale też wolałabym, aby Ktoś potwierdził

2 cze 22:27

23: a7 a jak wyliczyłeś AP ?

2 cze 22:28

a7: np. tak AP=x trójkąty ALK i NMK są podobne (k,k,k)

x		KM
	=
AL		KL

x
	{ua√2{2}
^a√3₂=Ua/2

	a√6
x=
	4

2 cze 22:48

a7:

	x		^a₂
miało być		=
	^a√3₂		^a√2₂

x=a√6/4

2 cze 22:51

23: A skąd znamy KL

2 cze 22:54

a7: KL można wyliczyć jako wysokość trójkąta równoramiennego o ramionach AS i SL równych a√3/2 i podstawie AS=a (AK=KS =a/2 i korzystamy z tw. Pitagorasa))

2 cze 22:57

23: No i tu mam problem, wychodzi ze K jest środkiem boku AS. Ja tego nie widzę jak to sensownie uzasadnić ?

2 cze 23:03

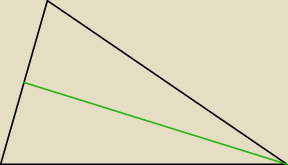
a7: no jak mamy trójkąt równoramienny to zawsze jego wysokość (ta prowadzona od równych sobie ramion) dzieli podstawę na pół

2 cze 23:18

a7: https://matematykaszkolna.pl/strona/500.html

2 cze 23:19

a7: tzn. wysokość prowadzona z wierzchołka w którym łączą się ramiona trójkąta równoramiennego dzieli podstawę na odcinki równej długości

2 cze 23:20

23: Ja rozumiem ale jaka jest pewnosc ze przebija ona K a nie przechodzi obok ?

2 cze 23:24

a7:

2 cze 23:24

a7: hmm, nie bardzo rozumiem czego nie rozumiesz, przecież ten trójkąt jest "konstruktem płaskim w 2D" i po prostu rysujemy jego wysokość

2 cze 23:26

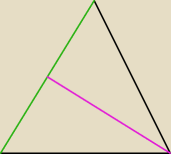
a7: wszystkie punkty, które tworzą ten trójkąt są na swoich miejscach, więc wysokość też będzie na swoim miejscu

2 cze 23:27

a7:

2 cze 23:27

23:

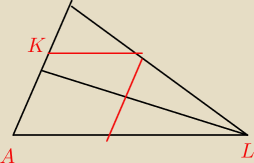
a tak byc nie moze?

2 cze 23:29

a7: a chyba rozumiem, też się nad tym zastanawiałam i zaraz Ci powiem jak to wykluczyłam

2 cze 23:30

23: Rozumiem ze ASL jest rownoramienny o ramionach AS i SL nie rozumiem tylko skad pewnosc ze jego wysokosc z L trafi w K

2 cze 23:31

a7: więc to trzeba inaczej zacząć, a mianowicie wiemy z treści zadania, że AS || PR i , że

	a
KM=		, wiemy, że KL jest pod kątem prostym do do AS czyli nasze KM=a/2 prowadzimy KR \|\|
	2

AL i dalej tak jak pisała Mila , że jest skala podobieństwa trójkątów ADE i KGF itd.

2 cze 23:37

a7: jeszcze się powtórzę trochę inaczej: jak mamy trójkąt ALS to wiemy, że KS jest pod kątem prostym, a odległość płaszczyzny (z treści zadania) też musi być pod kątem prostym czyli KM=a/2

2 cze 23:39

a7: *KL (nie KS) jest pod kątem prostym jako wysokość trójkąta ALS

2 cze 23:40

a7: AS || PR więc KR=MN=AP

2 cze 23:42

a7: ramiona są AL i LS

2 cze 23:42

a7: jest to "położony" trójkąt równoramienny na jednym z ramion czyli na ramieniu AL(ΔALS)

2 cze 23:44

23:

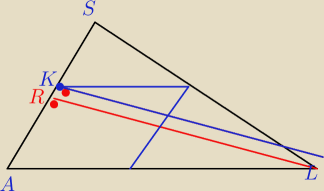
No piszesz ze wiemy ze KL jest pod katem prostym czyli stwierdzasz od razu KL że pokrywa sie z wykoscią a moze jest tak ja na rysunku wyzej ze jak poprowadze pod katem prostym do AS z wierzcholka K to nie trafi w L ?

2 cze 23:51

23: Ja nie widze ze KML są wspoliniowe tępy jestem

2 cze 23:53

a7: wydaje mi się, że jednak myślę poprawnie ja wybieram punkt K jako "punkt odniesienia" (nie mówiąc po matematycznemu) , dla punktu K (spodka wysokości trójkąta ALS) jest odległość 1/2 od płaszczyzny

2 cze 23:56

a7: najpierw rysujemy wysokość KL

2 cze 23:56

23: stop pytanie od razu

2 cze 23:57

a7: wiemy, że AS || PR tak?

2 cze 23:57

23: Rysuje Odcinek KL prostopadly do AS ale nie wiem czy pokrywa sie on z wysokoscią

2 cze 23:58

a7: odwrotnie

3 cze 00:00

a7: rysujesz wysokość KL

3 cze 00:00

a7: wiesz, że AS jest równoległe do PR, i że KM (część wysokości jest równe a/2, to wszystko wiesz z treści zadania i z wykonania właściwego rysunku)

3 cze 00:01

23: to wiem zgadza sie

3 cze 00:03

a7:

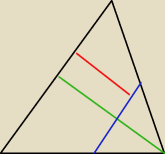
zielony odcinek to nasza wysokość, czerwony odcinek to Twój odcinek również równy a/2, ale trudno z niego coś wyliczyć

3 cze 00:04

a7: (w sensie czerwony również równy a/2 jak KM)

3 cze 00:05

23: czerwony to moj ktory prowadzi do punktu K ja twierdze ze K jest na koncu czerwonego

3 cze 00:06

23: Zgadza sie uwazam ze czerwony to KM przekonaj mnie ze on sie pokrywa z zieloną wysokoscią

3 cze 00:06

a7: to się nie rozumiemy, ja oznaczyłam jako K koniec wysokości, więc koniec wysokości jest w punkcie K,

3 cze 00:08

a7: chyba chodzi Ci o to , że mój K to nie jest K z rysunku Mili

3 cze 00:09

a7: ok spróbuję, ale nie wiem jak długo mi starczy cierpliwości

3 cze 00:10

23: No chyba oznaczenia pogubilismy poczekaj ja narysuje

3 cze 00:11

a7: spróbuj spojrzeć jeszcze raz na rysunek z 9:04 (z "moim" K) i zobacz , że KR =MN=AP, czy to Ci się zgadza?

3 cze 00:12

23:

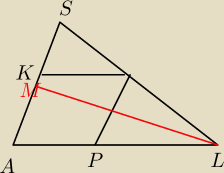
Trzymajmy sie rysunku MILI mamy na nim taka sytuacje zgadza sie ML jest wysokoscią tak ? Ale skad wiem ze M i K się nalożą?

3 cze 00:15

23: zgadza sie patrze

3 cze 00:16

23: na ten z 9:04

3 cze 00:16

a7: na rysunku Mili nie ma wysokości narysowanej jest tylko punkt K

3 cze 00:21

23: W sensie z punktu K moge poprowadzic pod katem prostym do AS odcinek

3 cze 00:22

a7: czy porozumieliśmy się już co do tego że ten trójkąt ALS jest równoramienny położony na ramieniu AL?

3 cze 00:22

23: tak to oczywiste bo boki to dwie wysokosci trojkata rownobocznego

3 cze 00:24

a7: czy rozumiemy że AL=SL=a√3/2 (są to wysokości ścian tego czworościanu)?, AS krawędź czworościanu od której płaszczyzna jest odległa o a/2 tak?

3 cze 00:25

a7: ok

3 cze 00:26

23: a7 czy twoje K na rysunku z 9:04 to te same co u Mili ? Bo to moze nie jest ten sam punkt i stad ja sie motam

3 cze 00:28

a7:

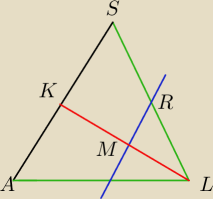
a już wiem chodzi Tobie nie o punkt K a o R skąd wiadomo, że KR || AL

3 cze 00:28

a7: z założenia miał być ten sam, ale teraz sama znów zaczęłam wątpić

3 cze 00:29

a7: ale to chyba można wyliczyć

3 cze 00:30

23: zaraz cos wrzuce

3 cze 00:34

23: jestes ?

3 cze 00:36

a7: ok

3 cze 00:36

23: Chodzi mi o to niby to rysunek Mili https://wrzucplik.pl/pokaz/2049696---vd3s.html

3 cze 00:37

23: I KL nie jest wysokoscią na nim o to mi ciagle chodzi

3 cze 00:37

a7: możesz wrzucić przez zapodaj, bo nie znam się czy wrzucplik nie bedzie mial jakiś wirusów itp

3 cze 00:38

a7: ?

3 cze 00:38

23: https://zapodaj.net/ed0e9020ecd01.jpg.html

3 cze 00:39

a7: widziałam rysunek, chyba rozumiem, w taki razie moje wyliczenia są prawie na pewno błędne, ale zaraz może się coś wymyśli

3 cze 00:41

23: a7 ja mysle ze Ty masz racje intuicja ale nie umiem uzasadnic ze K jest srodkiem.

3 cze 00:42

a7: właściwie to najlepiej jakby Mila lub Eta wytłymaczyły to zadanie, bo to podobno z matury, więc nie powinno być aż tak czasochłonne

3 cze 00:43

23: i pewnie tak, ale ma sens to o co pytam ?

3 cze 00:44

23: https://wrzucplik.pl/pokaz/2049702---cs7y.html Czy napewno nie bedzie tak jak na tym rysunku ze K nie pokryje sie ze spodkiem wysokosci ? I dlaczego.

3 cze 00:45

a7: czy możesz wrzucić przez zapodaj?

3 cze 00:47

23: https://zapodaj.net/95e7aee54ec65.jpg.html

3 cze 00:48

23: Dobra wrócę tu jutro może ktoś rozwieje watpliwosci emotka