26 lut 23:09
Eta:
Narazie , też nie wiem
........ myślę , myślę ......
26 lut 23:24
26 lut 23:30
Basia:
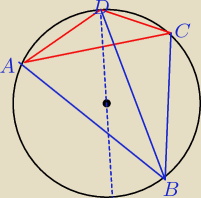
Na pewno jest to możliwe dla n=4, ale dalej ani rusz mi nie idzie
ostrokatne ABD i ABC
26 lut 23:34
27 lut 00:22
27 lut 00:27
Basia: Nikt nic nie wymyślił ?
Ja też nie.
Dobranoc
27 lut 02:40
tim: Jest i rozwiązanie przez Andrzeja.
27 lut 11:05
Andrzej: no tak... w sumie zadanie nie jest precyzyjnie sformułowane... warunek który podałem jest
konieczny, ale nie wiem do końca czy wystarczający. Powinni napisać "podaj warunek
wystarczający" albo "podaj warunek konieczny". Pomyślę jeszcze nad tym w wolnej chwili.
27 lut 11:13
edi: Dziękuję za zainteresowanie zadaniem z trójkątami
Szybko doszedłem do wniosku, że ilość trójkątów w zależności od pkt, to kolejne liczby
| | (n−2)(n−1)n | |
piramidalne. Stąd doszedłem do wzoru na ilość trójkątów w zależności od n: |
| . |
| | 6 | |
Warto zauważyć, że dla każdego n = 4k − 1, k∊N liczba trójkątów będzie nieparzysta, skąd
warunek z połową jest niespełniony.
Wiadomym jest też, że n ≥ 3.
Zastanawiam się, czy dla parzystej liczby trójkątów
zawsze można otrzymać układ, w którym
dokładnie połowa trójkątów będzie ostrokątna.
Pozdrawiam
27 lut 11:52
edi: Odświeżam
27 lut 20:15
edi: znowu odświeżam
Przepraszam za bycie nachalnym, ale muszę mieć odpowiedź na poniedziałek
27 lut 22:52
