nierówność w czworokącie
domin: W czworokącie wypukłym ABCD mamy |AB| + |BD| < |AC| + |CD|
Wykazać, że |AB| < |BC|
26 lut 21:06
Basia:
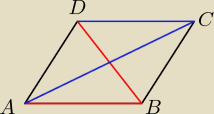
ABCD jest rombem
|AB|=|BC|=|CD|=|DA|=a
α=γ=60
wówczas
|BD|
2 = a
2+a
2−2a*a*cos60 = 2a
2−2a
2*
12 = 2a
2−a
2 = a
2
|BD|=a
|AC|
2 = a
2+a
2−2a*a*cos120 = 2a
2+2a
2*
12 = 3a
2
|AC| = a
√3
|AB|+|BD| = a+a=2a
|AC|+|CD|=a
√3+a = (1+
√3)a
czyli
|AB|+|BD|<|AC|+|CD|
natomiast
|AB|=a
|BC|=a
czyli |AB| nie jest mniejsze od |BC|
teza postawiona w Twoim zadaniu jest fałszywa
26 lut 23:58
R.W.16l: Twój rysunek jest beznadziejny, bo to nie musi być romb
W rombie AB + BD jest równe DC + CA, a nie mniejsze
dalej nie czytałem, ale już rysunek mnie zdziwił
27 lut 11:03
R.W.16l: chociaż nie, pomyliło mi się z kwadratem

27 lut 11:03
edi: Skąd wiadomo, że czworokąt jest rombem? oO
Ja próbowałem ruszyć to z nierówności trójkąta, ale kilkukrotnie dochodziłem do sprzeczności
27 lut 12:00
domin: witam
ja również próbowałem robić to z nierówności trójkąta, ale też nie wychodziło
Skąd wiadomo, że jest rombem − nie wiadomo, Basia rozpatruje szczególny przypadek. Zdaje
się, że zadanie (nie?)rozwiązane. W jego treści musi być błąd.
Pozdrawiam
27 lut 13:47
 ABCD jest rombem
|AB|=|BC|=|CD|=|DA|=a
α=γ=60
wówczas
|BD|2 = a2+a2−2a*a*cos60 = 2a2−2a2*12 = 2a2−a2 = a2
|BD|=a
|AC|2 = a2+a2−2a*a*cos120 = 2a2+2a2*12 = 3a2
|AC| = a√3
|AB|+|BD| = a+a=2a
|AC|+|CD|=a√3+a = (1+√3)a
czyli
|AB|+|BD|<|AC|+|CD|
natomiast
|AB|=a
|BC|=a
czyli |AB| nie jest mniejsze od |BC|
teza postawiona w Twoim zadaniu jest fałszywa
ABCD jest rombem
|AB|=|BC|=|CD|=|DA|=a
α=γ=60
wówczas
|BD|2 = a2+a2−2a*a*cos60 = 2a2−2a2*12 = 2a2−a2 = a2
|BD|=a
|AC|2 = a2+a2−2a*a*cos120 = 2a2+2a2*12 = 3a2
|AC| = a√3
|AB|+|BD| = a+a=2a
|AC|+|CD|=a√3+a = (1+√3)a
czyli
|AB|+|BD|<|AC|+|CD|
natomiast
|AB|=a
|BC|=a
czyli |AB| nie jest mniejsze od |BC|
teza postawiona w Twoim zadaniu jest fałszywa
