Kwadrat ABCD o boku długości a jest podstawą ostrosłupa ABCDS czarniecki: Kwadrat ABCD o boku długości a jest podstawą ostrosłupa ABCDS. Krawędz boczna AS ma również długość a i jest prostopadła do płaszczyzny podstawy. Ostrosłup ten przecięto płaszczyną przechodzącą przez wierzchołek A i prostopadłą do krawędzi CS. Oblicz pole otrzymanego przekroju.

	a √3
Obliczyłem, że dłuższa przekątna ma		, ale nie wiem jak obliczyć drugą.
	6

czarniecki: Ktoś, coś?

Mila: Po 20

annabb:

	a√6		a√2
dłuższa ma		a druga ma
	3		2

Mila: Potrzebna jeszcze pomoc?

czarniecki: tak

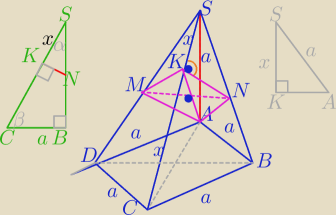
Mila: 1) MN||DB AK⊥SC |SC|=a√3, |AC|=a√2, |D|=|SB|=a√2⇔ΔDBS−Δrównoboczny ⇔ΔMNS−Δrównoboczny

	1		a2√2
PΔACS=		*a√2*a=
	2		2

a2√2		1
	=		*|SC|*|AK|
2		2

a²√2=a√3*|AK| ⇔a√2=√3*|AK| /*√3 a√6=3*|AK|

	a√6
|AK|=
	3

========== 2) WΔAKS: |KS|=x a²=x²+|AK|²

	a√3
x=
	3

3)ΔSKN∼ΔCBS⇔

x		SB
	=
SN		SC

stąd:

	a√2
|SN|=
	2

	a√2
|MN|=
	2

============== Inny rysunek (może lepiej widać?)

Mila: https://matematykaszkolna.pl/forum/292292.html

Mila: https://matematykaszkolna.pl/forum/383715.html

Mila: Niepotrzebnie pisałam, bo już jest rozwiązane, ale zapomniałam, bo to dawno było.