stereometria
pomocy: Kwadrat ABCD o boku długości a jest podstawą ostrosłupa ABCDS. Krawędź boczna AS ma również
długość a i jest prostopadła do płaszczyzny podstawy. Ostrosłup ten przecięto płaszczyzną
przechodzącą przez wierzchołek A i prostopadłą do krawędzi CS. Oblicz pole otrzymanego
przekroju.
Wedle odpowiedzi otrzymanym przekrojem ma być deltoid, ale nie rozumiem, skąd biorą się te
odcinki równej długości?
Czy ktoś mógłby to wyjaśnić?
10 sty 20:43
wredulus_pospolitus:
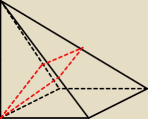
Należy zauważyć, że |BS| = |DS| (co wynika z tego, że AS prostopadłe do podstawy ... albo jak
wolisz Δ
ABS i Δ
ADS są prostokątne i oba maja przyprostokątne wynoszące 'a'
10 sty 21:46
Mila:
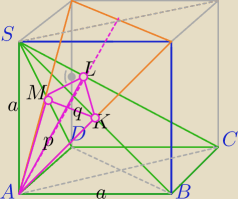
1) Umieszczamy ostrosłup w sześcianie, może lepiej będzie wszystko widać:
SC jest przekątną sześcianu, przekrój prowadzimy prostopadle do SC
AL⊥SC
MK ||DB, MK⊥AL
Przekrojem jest deltoid AKLM
2)
|SC|=a
√3
|DB|=a
√2
3) długość |AL|=p
Pole ΔACS na dwa sposoby:
a
√2*a=a
√3*p
a
√2=
√3*p /*
√3
4)
Długość MK
spróbuj sam
10 sty 22:16
 Należy zauważyć, że |BS| = |DS| (co wynika z tego, że AS prostopadłe do podstawy ... albo jak
wolisz ΔABS i ΔADS są prostokątne i oba maja przyprostokątne wynoszące 'a'
Należy zauważyć, że |BS| = |DS| (co wynika z tego, że AS prostopadłe do podstawy ... albo jak
wolisz ΔABS i ΔADS są prostokątne i oba maja przyprostokątne wynoszące 'a'
 1) Umieszczamy ostrosłup w sześcianie, może lepiej będzie wszystko widać:
SC jest przekątną sześcianu, przekrój prowadzimy prostopadle do SC
AL⊥SC
MK ||DB, MK⊥AL
Przekrojem jest deltoid AKLM
2)
|SC|=a√3
|DB|=a√2
3) długość |AL|=p
Pole ΔACS na dwa sposoby:
1) Umieszczamy ostrosłup w sześcianie, może lepiej będzie wszystko widać:
SC jest przekątną sześcianu, przekrój prowadzimy prostopadle do SC
AL⊥SC
MK ||DB, MK⊥AL
Przekrojem jest deltoid AKLM
2)
|SC|=a√3
|DB|=a√2
3) długość |AL|=p
Pole ΔACS na dwa sposoby: