Ostrosłup zadanie maturalne.
Greg:
Witam mam zadanie z matury próbnej nowa era 2015 styczeń matematyka rozszerzona, nie ma nigdzie
odpowiedzi do tych zadań a jedno sprawia mi trudność i nie mogę ruszyć coś z nim.
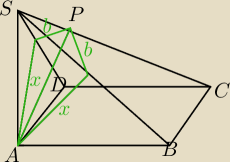
Kwadrat ABCD o boku długości a jest podstawą ostrosłupa ABCDS. Krawędź boczna AS ma również
długość a i jest prostopadła do płaszczyzny podstawy. Ostrosłup ten przecięto płaszczyzną
przechodzącą przez wierzchołek A i prostopadłą do krawędzi CS. Oblicz pole otrzymanego
przekroju.
Doszedłem do tego że odcinek AP ma długość a
√6/3 a także odcinek SC to a
√3 to co udało mi
się ustalić zaznaczyłem na rysunku, z moich obliczeń wynika również, że kąt ASC jest taki sam
jak PAC, ale już sam nie wiem co to wnosi, utnkąłem w martwym punkcie, za dużo przemyśleń mam
w głowie i to powoduje chaos. Przydałoby mi się jakieś świeże spojrzenie

2 maj 23:59
losiu_09: Ściana ABS jest trojaktem rownoramiennym wiec SB=a
√2. Z Pitagorasa w trACS mamy
SC
2=AC
2+AS
2= (a
√2)
2+a
2= 3a
2 . zauwazamy ze przekroj jest deltoidem wiec musimy
policzyc jego przekatne . Dalej sam nie wiem ale trzeba pokombinować . przekatna PA jest
prostopadła do SC mozna z tego jakos skorzystać . chcociaz sam nie wiem czy pomogłem jakoś

3 maj 00:38
losiu_09: Przekatna AP mozesz wyznaczyc z pola trojkata prostokatnego PΔSCA= 1/2 * SC* AP = 1/2 * SA* AC
. a * a√2 = a√3 * AF .. AF= a√63
3 maj 00:46
3 maj 00:52
Greg: Tak tak, napisałem że to mam

, że odcinek AP ma długość taką właśnie a
√6/3. Tylko właśnie
potrzebuje tej drugiej przekątnej deltoidu, lub boków x i b oraz kąta pomiędzy nimi.
3 maj 01:17
Greg: Widzę też, to że trójkąt DBS jest równoboczny a ta druga przekątna jest równoległa do jego
podstawy DB, tyle że nie wiem na jakiej jest ona wysokości.
3 maj 01:18
Marta: Na pewno dobrze narysowałeś przekrój? Z zadania wynika, że cała płaszczyzna jest prostopadła
do tej krawędzi

3 maj 10:11
3 maj 12:09
Stanisław: Skąd wziąć drugą przekątną, dlaczego a
√2/2 ? też mam maturę w przyszłym tygodniu

3 maj 14:12
Greg: mhm, czyli mowisz, że ta druga przekątna jest w połowie wysokości trójkąta DBS który jest
równoboczny, a że jego bok to a√2 to w połowie jest połowa z tego. Tylko z których
pitagorasów to wynika, (to że na prawdę jest to połowa) bo ja nie widzę :c
3 maj 14:30
Greg: re
3 maj 20:27
Mila:
Greg idź spać.
Powodzenia na maturce.
Zadanko się zrobi przed piątkiem. We wtorek takiego nie będzie.
3 maj 21:03
Qulka:
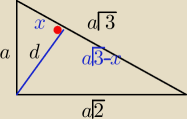
poszukaj na forum ze 3 razy było
a pitagorasy
a
2=x
2+d
2
2a
2=3a
2−2a
√3x+x
2+d
2
d=a
√2/3
3 maj 21:29
Qulka:
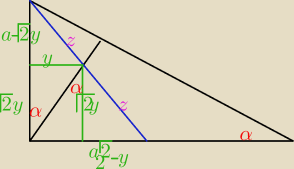
aa to ta druga miała być

to z podobieństwa
y=a
√2 / 4
więc są takie same zatem z=z i jak namalujesz drugi przekrój to ta przekątna d
2 będzie w
połowie
3 maj 22:09
Greg: Który to jest trójkąt? Mógłbym prosić o jakieś oznaczenie go ?

bo nie mogę go znaleźć na
rysunku.
4 maj 21:00
Mila:
Czekaj, nie wchodzi mi rysunek. Będę próbować za chwilę wkleić.
4 maj 21:55
Mila:
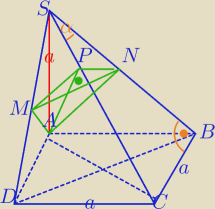
|AS|=a
|SB|=|SD|=|AC|=a
√2
|SC|
2=a
2+(a
√2)
2
|SC|=a
√3
ΔSBC− Δprostokątny
W ΔSAC:
|AP|*|SC|=|AS|*|AC|
|AP|*a
√3=a*a
√2
W ΔAPS:
a
2=|AP|
2+|SP|
2
W ΔSBC:
| | |SB | | a√2 | | √6 | |
cosα= |
| = |
| = |
| |
| | |SC| | | a√3 | | 3 | |
PN⊥SC
W ΔSPN:
|SN|=|MN|
4 maj 21:58
Mila:
5 maj 19:47
Qulka: mój ten sam co wyżej (ACS) tylko dodatkowo niebieska linia przecięcia z przekrojem SDB
5 maj 21:46
Mila:
Wiem,
Quleczko, ale zdaje się, że nie "widział".

5 maj 22:30
5 maj 22:31
Qulka: ale dopisałam jakby za tydzień znów ktoś o to pytał bo to już chyba 5 post z tym zadaniem

5 maj 22:32
Mila:
Podoba mi się to zadanie i wtrąciłam się.
5 maj 22:42
Greg: Dzięki wam bardzo za pomoc. Mila − bardzo ładnie, czytelnie rozpisane daje okejke

.
Matura rozszerzona nie była jednak tak wymagająca jak to zadanie

9 maj 17:11
Kacper:
:

9 maj 17:20
Mila:
Trening zawsze daje dobre wyniki.

9 maj 23:43
Deni: Skąd wiemy że SN jest prostopadły do SP?
15 lut 18:36
Deni: Znaczy PN do SC
15 lut 18:37
 Witam mam zadanie z matury próbnej nowa era 2015 styczeń matematyka rozszerzona, nie ma nigdzie
odpowiedzi do tych zadań a jedno sprawia mi trudność i nie mogę ruszyć coś z nim.
Kwadrat ABCD o boku długości a jest podstawą ostrosłupa ABCDS. Krawędź boczna AS ma również
długość a i jest prostopadła do płaszczyzny podstawy. Ostrosłup ten przecięto płaszczyzną
przechodzącą przez wierzchołek A i prostopadłą do krawędzi CS. Oblicz pole otrzymanego
przekroju.
Doszedłem do tego że odcinek AP ma długość a√6/3 a także odcinek SC to a√3 to co udało mi
się ustalić zaznaczyłem na rysunku, z moich obliczeń wynika również, że kąt ASC jest taki sam
jak PAC, ale już sam nie wiem co to wnosi, utnkąłem w martwym punkcie, za dużo przemyśleń mam
w głowie i to powoduje chaos. Przydałoby mi się jakieś świeże spojrzenie
Witam mam zadanie z matury próbnej nowa era 2015 styczeń matematyka rozszerzona, nie ma nigdzie
odpowiedzi do tych zadań a jedno sprawia mi trudność i nie mogę ruszyć coś z nim.
Kwadrat ABCD o boku długości a jest podstawą ostrosłupa ABCDS. Krawędź boczna AS ma również
długość a i jest prostopadła do płaszczyzny podstawy. Ostrosłup ten przecięto płaszczyzną
przechodzącą przez wierzchołek A i prostopadłą do krawędzi CS. Oblicz pole otrzymanego
przekroju.
Doszedłem do tego że odcinek AP ma długość a√6/3 a także odcinek SC to a√3 to co udało mi
się ustalić zaznaczyłem na rysunku, z moich obliczeń wynika również, że kąt ASC jest taki sam
jak PAC, ale już sam nie wiem co to wnosi, utnkąłem w martwym punkcie, za dużo przemyśleń mam
w głowie i to powoduje chaos. Przydałoby mi się jakieś świeże spojrzenie 

 , że odcinek AP ma długość taką właśnie a√6/3. Tylko właśnie
potrzebuje tej drugiej przekątnej deltoidu, lub boków x i b oraz kąta pomiędzy nimi.
, że odcinek AP ma długość taką właśnie a√6/3. Tylko właśnie
potrzebuje tej drugiej przekątnej deltoidu, lub boków x i b oraz kąta pomiędzy nimi.


 poszukaj na forum ze 3 razy było
a pitagorasy
a2=x2+d2
2a2=3a2−2a√3x+x2+d2
d=a√2/3
poszukaj na forum ze 3 razy było
a pitagorasy
a2=x2+d2
2a2=3a2−2a√3x+x2+d2
d=a√2/3
 aa to ta druga miała być
aa to ta druga miała być  to z podobieństwa
to z podobieństwa
 bo nie mogę go znaleźć na
rysunku.
bo nie mogę go znaleźć na
rysunku.
 |AS|=a
|SB|=|SD|=|AC|=a√2
|SC|2=a2+(a√2)2
|SC|=a√3
ΔSBC− Δprostokątny
W ΔSAC:
|AP|*|SC|=|AS|*|AC|
|AP|*a√3=a*a√2
|AS|=a
|SB|=|SD|=|AC|=a√2
|SC|2=a2+(a√2)2
|SC|=a√3
ΔSBC− Δprostokątny
W ΔSAC:
|AP|*|SC|=|AS|*|AC|
|AP|*a√3=a*a√2


 .
Matura rozszerzona nie była jednak tak wymagająca jak to zadanie
.
Matura rozszerzona nie była jednak tak wymagająca jak to zadanie 

