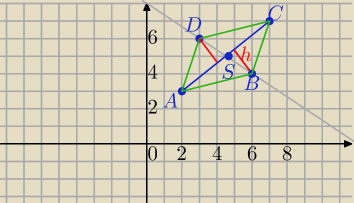
Wyznacz współrzędne wierzchołków B i D matura2k20: Odcinek AC, gdzie A = (2,3) oraz C = (7,7), jest przekątną równoległoboku ABCD. Przekątna BD tego równoległoboku zawiera się w prostej o równaniu y = −²₃ + 8 Wyznacz współrzędne wierzchołków B i D wiedząc, że pole tego równoległoboku jest równe 11. Proszę o jakieś wskazówki bo już przerobiłem to na wiele sposobów i nic logicznego nie wychodzi. Jedyne pewniaczki jakie mam to długość AC = √41 i punkt przecięcia przekątnych to (⁹₂, 5).

ICSP: https://matematykaszkolna.pl/forum/400835.html Skąd wy bierzecie te zadania

ford: https://matematykaszkolna.pl/forum/399794.html

matura2k20: e−trapez... potężny kurs, ale czasem zadania są taką zagwostką że się w głowie nie mieści, dzięki wielkie

Mila:

	2
A = (2,3) oraz C = (7,7), y=−		x+8
	3

1)|AC|=√5²+4²=√41

	11		1
P▱=11⇔P ΔABC=		=		|AC|*h
	2		2

1		11		11
	*√41*h=		⇔h=		− odległość punktu B od prostej AC
2		2		√41

2) Prosta AC: 3=2a+b i 7=7a+b −−−−−−−−−−−−−−−−−

	4		7		4		7
−4=−5a⇔a=		, b=		⇔ y=		x+		/*5⇔
	5		5		5		5

4x−5y+7=0

	2
4) Odległość punktu B=(b, −		b+8) od prostej AC:
	3

	11		2   |4*b−5*(− b+8)+7|   3
d=		=
	√41		√41

	10
|4b+		b−33|=11
	3

	22
|		b−33|=11⇔
	3

b=3 lub b=6 Mamy punkty: B(6,4) , D(3,6) ============