rownoleglobok , geometria
dzejbi: Odcinek AC , gdzie A = (2,3) oraz C = (7,7) , jest przekątną równoległoboku ABCD.Przekątna BD
| | 2 | |
tego równoległoboku zawiera się w prostej o równaniu y=− |
| x+8 .Wyznacz współrzędne |
| | 3 | |
wierzchołków B i D wiedząc, że pole tego równoległoboku jest
równe 11.
4 maj 14:29
dzejbi: obliczyłem sobie środek przecięcia przekątnych |AC|
4 maj 14:42
Gangster: Przekatne przecinaja sie pod katem prostym, majac pole policzysz najpierw polowe przekatnej BD.
Pozniej liczysz dlugosc odcnika BS i SD, sa one rownej dlugosci.
4 maj 15:05
dzejbi: w równolegloboku też przecinaja się pod kątem prostym? wiem że na 100% w rombie
4 maj 15:08
Gangster: przeczytalem romb sorry, to nie przecinaja sie pod katem 90, ale połowią się. Dzisiaj nie jest
mój dzien widze.
4 maj 15:12
dzejbi: nom luzik
4 maj 15:22
Eta:
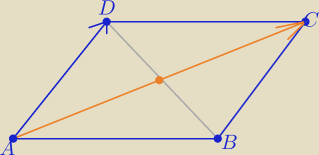
| | 2 | |
AC→= [5,4] i D(x, − |
| x+8) |
| | 3 | |
| | 2 | |
P=11 ⇒ |5(− |
| x+5)−4(x−2)|=11 /*3 |
| | 3 | |
|−10x+75−12x+24|=33
................
dokończ
4 maj 15:40
salamandra: można to zrobić klasycznie bez wektorów? bo zainteresowało mnie to zadanie, ale nie mogłem
znaleźć pomyslu
4 maj 15:47
f123: Mozna, liczysz dlugosc polowy przekatnej DB, a nastepnie odleglosc od przeciecia sie
przekatnych do punktu D musi byc ta wartosica. Dostajesz dwa punkty D I B
4 maj 15:50
Eta:
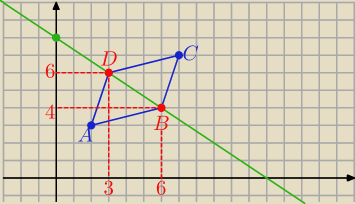
4 maj 15:50
salamandra: No właśnie, ale jak policzyć połowę DB mając tylko S?
4 maj 15:50
Eta:
Co to znaczy "klasycznie", bez wektorów ?

4 maj 15:52
salamandra: czyli bez wektorów

4 maj 15:52
Eta:
Wektory w geometrii analitycznej baaaaaaaaardzo upraszczają rozwiązania !
co widać w moim wpisie

4 maj 15:53
salamandra: Gorzej, jeśli się ich nie rozumie i chciałoby się inaczej rozwiązać

to da się czy nie da?

bo nie wiem jak obliczyć długość połowy DB mając tylko S?
4 maj 15:54
f123: Liczymy kat pomiedzy dwoma prostymi
4 maj 15:55
Eta:
Też tak można ( ale po co? wyciągać
armatę do zabicia
muszki 
4 maj 15:57
dzejbi: o dziękuje bardzo

4 maj 16:00
salamandra: To gdybys Eto była tak uprzejma wytłumaczyć to rozwiazanie z wektorami, byłbym wdzięczny

4 maj 16:05
ICSP: Nie bądź!
Niech sam przemyśli!
4 maj 16:09
salamandra: Nie rozumiem jedynie tego wzoru z modułem
4 maj 16:11
ICSP: Masz dwa wektory które rozpinają równoległobok:
a = [ax , ay]
b = [bx , by]
wtedy pole tego równoległoboku jest równe wartości bezwzględnej z wyznacznika macierzy
zbudowanej z tych współrzędnych:
W = | ax ay | bx by| = axby − bxay
P = |W| = ...
4 maj 16:16
f123: To ja podrzucem z katem:
Prosta AS
| 1066 | | 2 | |
| = √(4.5 − x)2 + ( |
| x − 3)2 |2 |
| 2√21853 | | 3 | |
| 1136356 | | 81 | | 4 | |
| = |
| − 9x + x2 + |
| x2 − 4x + 9 |
| 349648 | | 4 | | 9 | |
| 13 | | 81 | | 4 | |
| = |
| − 9x + x2 + |
| x2 − 4x + 9 |
| 4 | | 4 | | 9 | |
Mnozysz razy 9, wyliczasz x i koniec zadania
4 maj 16:24
dzejbi: Przeglądając wasze odpowiedzi sam doszedłem do jeszcze jednej:
P
ABCD=11
P
ABCD=2*P
ACD
| | 1 | |
PABC= |
| |(xb−xa)(yc−ya)−(yb−ya)(xc−xa) |
| | 2 | |
| | 1 | | 1 | | 2 | |
5 |
| = |
| |(x−2)(7−3)−(− |
| x+8−3)(7−2)| |
| | 2 | | 2 | | 3 | |
...
...
x=6 v x=3
podstawiam i mam 2 punkty

4 maj 17:07
salamandra: 
4 maj 17:10





 to da się czy nie da?
to da się czy nie da?  bo nie wiem jak obliczyć długość połowy DB mając tylko S?
bo nie wiem jak obliczyć długość połowy DB mając tylko S?




