Stereo
jaros:
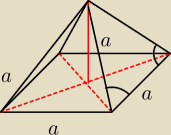
W ostrosłupie prawidłowym czworokątnym kąt między dwiema przeciwległymi krawędziami bocznymi ma
miarę 60°, a objętość tego ostrosłupa wynosi V. Oblicz odległość środka podstawy ostrosłupa od
krawędzi bocznej.
Czy kąty są dobrze zaznaczone?
3 kwi 23:17
Eta:
Źle
3 kwi 23:28
Mila:
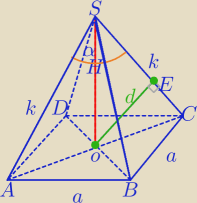
α=60
o⇒
ΔACS− Δrównoboczny
Próbuj dalej sam
3 kwi 23:30
Eta:
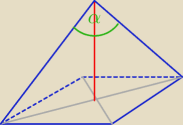
3 kwi 23:31
Szkolniak:
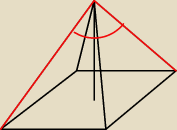
3 kwi 23:33
Eta:
Ooo
Mila już z gotowcem wystartowała

3 kwi 23:33
Mila:
Z jakim gotowcem? To podpowiedź

3 kwi 23:47
jaros: Dziewczyny a wiecie co mi tu może pomóc ten kont? nie chce gotowca jak coś

4 kwi 00:05
salamandra: to, że wiesz, że krawędź boczna jest równa przekątnej podstawy
4 kwi 00:11
jaros: Z jakiej to jest własności?
4 kwi 00:12
jaros: coz z tw cos?
4 kwi 00:13
salamandra: zauważ, że AS=SC, to wiesz z czego tak?
4 kwi 00:14
jaros: no tak bo czworokąt prawidłowy jest w podstawie tzn kwadrat
4 kwi 00:18
salamandra: Co to ma do rzeczy?

AS i SC to krawędzie boczne
4 kwi 00:21
jaros: No tak właśnie tak ale skąd wiemy że krawędź boczna jest równa krawędzi podstawy

4 kwi 00:25
salamandra: Nie krawędzi podstawy, tylko przekątnej podstawy. Skoro krawędzie boczne są równe i kat miedzy
nimi w trojkącie ASC jest równy 60, to na pewno jest to trojkat równoramienny, wiec katy przy
podstawie ma równe, wiec te katy maja miarę (180−60)/2, czyli 60, stad wniosek ze jest to
nawet trojkat równoboczny, a nie tylko równoramienny
4 kwi 00:29
Eta:
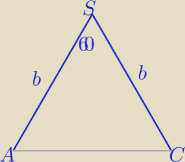
|AC|= ?
4 kwi 00:30
jaros: a
√2 przecież i z tego oraz kąta wyliczyć a?

4 kwi 00:40
salamandra: 
już nie wiem jak mam ci wytłumaczyć
4 kwi 00:47
Jaros: No ale co źle napsiałem?
4 kwi 00:59
salamandra: Uzależnij przekątna podstawy od k z rysunku Mili
4 kwi 01:02
Jaros: Ale to jest enigmatyczne zadanie... dobrze uzależnić zmienne od siebie, lecz jak wspominałeś
jest to trojkat równoboczny to co ty tam chcesz uzależniać? Że k = a
√2
4 kwi 01:06
Jaros: 
4 kwi 01:31
4 kwi 03:14
4 kwi 03:16
jaros: A człeczego nie można odległości uzależnić np od pola podstawy?
4 kwi 11:29
Eta:
W treści masz podane V , więc d uzależniasz od V

4 kwi 11:32
jaros: A jakby w twoim rozwiązaniu zamiar dp użyć po prostu zmiennej a tzn. dp = a√2 wynik będzie
troszkę inny ale tez prawidłowy tak?
4 kwi 11:47
jaros: Ktoś mi powie co robie źle?
1) wyznaczam h od długości podstawy tzn a
√2
2) Uzależniam d od a
a
√6 = 4d
Liczę P
p, hmm i tu mam zagwostkę; Pp = U{a
2√3{4}
| | | | 2√3d2 | |
i teraz |
| = |
| i czy jest jakiś błąd jak narazie? |
| | 4 | | 3 | |
4 kwi 12:04
Eta:
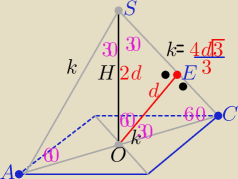
Echhhh

| | 4d√3 | | 16d2 | |
W ΔOCS "ekierkowym" : H=2d , k= |
| , k2= |
| |
| | 3 | | 3 | |
| | k2 | |
Pp= |
| −− pole kwadratu za pomocą dł. przekątnej k |
| | 2 | |
| | 1 | | 8d2 | | 16d3 | | 64d3 | |
V= |
| * |
| *2d⇒ V= |
| = |
| |
| | 3 | | 3 | | 9 | | 36 | |
to
============
i po ptokach

( wyliczanie "a" jest zbędne!)
4 kwi 12:04
Eta:
Po diabła Ci to "a" !
4 kwi 12:05
jaros: Bo nie wpadł bym na maturze, że za przekątną podstawy mogę podstawić d
p i liczyć z tym

Chwileczkę, to k jest długością krawędzi to dlaczego liczymy pole podstawy z tego?
4 kwi 12:08
salamandra: k jest zarowno krawedzia boczna i przekatna podstawy
4 kwi 12:09
Eta:
ΔACS jest równoboczny z treści zadania !
4 kwi 12:10
jaros: | | 1 | |
Ale jak to liczymy z przekątnej pole nie rozumiem i skąd ta |
| jak liczymy pole podstawy |
| | 2 | |
kwadratu?
4 kwi 12:11
salamandra: | | 1 | |
Pczworokąta= |
| *d1*d2*sinα, gdzie α− kąt zawarty między przekątnymi, w tym wypadku α=90, |
| | 2 | |
więc sin90=1
4 kwi 12:12
Eta:
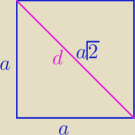
| | d2 | | d2 | |
P□=a2 lub P□= |
| bo d2=2a2 ⇒ |
| =a2=P |
| | 2 | | 2 | |
4 kwi 12:14
jaros: Aaaaa z tego no rozumiem

, a ktoś chętny poprowadzić wynik obliczeń z tym a
√2 bo ja juz
nawet nie wiem czy tamto jest doże a chciałbym wiedzieć czy tak sie da

4 kwi 12:14
jaros: A jeszcze jedno pytanie jak w ΔEOS przy kącie 30 stopni długość boku powinna wynosić d√3 a
cała długość odcinka (zakładając, że d dzieli bok ISCI na 2 równe części) nie powinna wynosić
2d√3?
4 kwi 12:17
Eta:
Tak często zastanawiam się ,kto Was uczy matematyki?
pewnie woźny po licencjacie ?

4 kwi 12:22
jaros: Wydaje mi się że to moja wina, iż za mało się przykładam oraz nigdy nie byłem orłem z matmy

4 kwi 12:24
Eta:


4 kwi 12:26
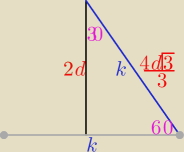
jaros: A wytłumaczysz mi jeszcze tą krawędź boczną?

4 kwi 12:26
Eta:
4 kwi 12:30
Eta:
Czy teraz jasne ?
4 kwi 12:48
jaros: No ale jak to tutaj wychodzi.... :'((((((
4 kwi 12:52
jaros: Hmmm jak mówiłem dokończę tu rozwiązanie z tym a
| | 2d√6 | | 8d2 | |
Pp = a2 = ( |
| )2 = |
| |
| | 3 | | 3 | |
| | 1 | | 8d2 | | 16d3 | |
V = |
| * |
| * 2d = |
| no i potem wyznaczamy wynik dla d |
| | 3 | | 3 | | 8 | |

4 kwi 13:24
Eta:
Ok

tylko po co ? w dobie pandemii chcesz jechać : z Warszawy do Lublina przez Rzym ?
4 kwi 13:29
marcin: Nie hahah jako dla mnie ten osób jest bardziej "czytelny"

4 kwi 13:32
marcin: O cholera wydało sie
4 kwi 13:32
Eta:

4 kwi 13:38
 W ostrosłupie prawidłowym czworokątnym kąt między dwiema przeciwległymi krawędziami bocznymi ma
miarę 60°, a objętość tego ostrosłupa wynosi V. Oblicz odległość środka podstawy ostrosłupa od
krawędzi bocznej.
Czy kąty są dobrze zaznaczone?
W ostrosłupie prawidłowym czworokątnym kąt między dwiema przeciwległymi krawędziami bocznymi ma
miarę 60°, a objętość tego ostrosłupa wynosi V. Oblicz odległość środka podstawy ostrosłupa od
krawędzi bocznej.
Czy kąty są dobrze zaznaczone?
 α=60o⇒
ΔACS− Δrównoboczny
Próbuj dalej sam
α=60o⇒
ΔACS− Δrównoboczny
Próbuj dalej sam





 AS i SC to krawędzie boczne
AS i SC to krawędzie boczne

 |AC|= ?
|AC|= ?

 już nie wiem jak mam ci wytłumaczyć
już nie wiem jak mam ci wytłumaczyć




 Echhhh
Echhhh 
 ( wyliczanie "a" jest zbędne!)
( wyliczanie "a" jest zbędne!)
 Chwileczkę, to k jest długością krawędzi to dlaczego liczymy pole podstawy z tego?
Chwileczkę, to k jest długością krawędzi to dlaczego liczymy pole podstawy z tego?

 , a ktoś chętny poprowadzić wynik obliczeń z tym a√2 bo ja juz
nawet nie wiem czy tamto jest doże a chciałbym wiedzieć czy tak sie da
, a ktoś chętny poprowadzić wynik obliczeń z tym a√2 bo ja juz
nawet nie wiem czy tamto jest doże a chciałbym wiedzieć czy tak sie da 







 tylko po co ? w dobie pandemii chcesz jechać : z Warszawy do Lublina przez Rzym ?
tylko po co ? w dobie pandemii chcesz jechać : z Warszawy do Lublina przez Rzym ?

