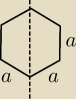
Jak to obliczyć? Tired ;~|: Oblicz pola powierzchni brył obrotowych otrzymanych przez obrot szesciokata foremnego o boku a wokol a) prostej przechodzacej przez środki przeciwleglych bokow szesciokąta b) prostej zawierajacej dłuższa przekatna szesciokata c) prostej zawierajacej bok szesciokata

a7: a) mamy walec o promieniu a√3/2 i wysokości a oraz dwa stożki o promieniu a√3/2 i tworzącej a (wysokościa/2)

	√3		√3		a
π(a		)2*a+2*π(a		)2*		=...........
	2		2		2

a7: to było b)

wredulus_pospolitus: (a) dwa 'ścięte stożki o średnicy = główna przekątna sześciokąta (c) walec o promieniu 'krótsza przekątna' sześciokąta + dwa stożka o tym samym promieniu − dwa stożki o połowę mniejszym promieniu

a7: b) miałoby być pole powierzchni ech

a7: https://matematykaszkolna.pl/strona/1003.html https://matematykaszkolna.pl/strona/1002.html

a7: b) 2πr+2πrl=2πr(1+l)=a√3π(1+a) ?

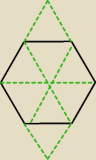
a7: a) 2πrl−2π(r/2)l=πrl=2a²π ?

a7:

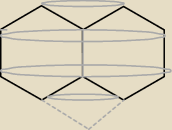
	√3
2πa√3*a+2*πa√3*2a−2πa		*a=5a2√3π
	2

Tired ;~|: Powinno wyjść w a) 3,5πα² b) 2√2πa² c) 6√2πa²

Tired ;~|: *b)2√3πa²

a7: ale tak jest w książce czy tak wyszło komuś?

Tired ;~|: w książce https://imgur.com/Igs6bfT

Tired ;~|: [img]https://i.imgur.com/Igs6bfT.png[/img]

Tired ;~|: ups, nie ma kodowania takiego

a7: ?

a7: c) 6√3πa²

a7: ok w a) już widzę błąd

a7:

	a		a
2πa*2a−2π		*a+2π(		)2=3,5πa2
	2		2

trzeba od dwóch stożków odjąć dwa mniejsze i dodać jeszcze "pokrywki"

a7: to było a) teraz b)

	a√3
2πU{a√3{2}*a+2π		*a=2√3πa2
	2

trzecie może sprobuj sam(a policzyć

a7:

	a√3		a√3
c)2πa√3*a+2πa√3*2a−2π		*a+2π		*a=6√3πa2
	2		2