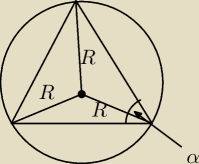
stereometria salamandra: Zadanie: W stożku obrotowym kąt nachylenia tworzącej do płaszczyzny podstawy ma miarę α. Na stożku opisano kulę o promieniu R. Oblicz objętość i pole powierzchni całkowitej tego stożka. Z czego tu skorzystać, skoro nie mam pewności, że ten promień to dwusieczna kąta α, bo jest okrąg opisany, a nie wpisany?

a7: https://matematykaszkolna.pl/strona/541.html R={a}{2sinα} ?

a7:

	a
R=
	2sinα

salamandra: Nigdy nie mogę tego zapamiętać, dzięki! Zaraz spróbuję

salamandra: No tak, ale wtedy nie wyznaczę podstawy tego stożka, bo muszę wziąć bok naprzeciwko kąta α?

a7: https://matematykaszkolna.pl/forum/322798.html

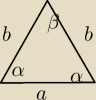
salamandra: mogę tak?

	b
R=
	2sinα

b=R*2sinα β=180−2α

	a
R=
	2sin(180−2α

a=R*2sin2a

salamandra: Wybacz, pisałem przed Twoim wpisem, już zerkam

a7: zajrzyj do linku

a7: ok

salamandra: Zostając na razie przy swoim: a=R*2sin(2α)

	1
(		a)2+H2=b2
	2

R²*sin²2α+H²=R²*2sin²α mogę tak też czy nie wyjdzie?

salamandra: zrobiłem tak jak w linku: H=R*2sin²α

	1
Pp=(		a)2*π = π*(Rsin(2a))2= R2*sin22α*π
	2

Pb=π*Rsin(2α)*R*2sinα=Rπ*4sin(2α)sin(α)

	1		1
V=		*R2*sin2(2α)π*R2sin2α=		R3π*sin2(2α)*2sin2(α)
	3		3

To jest źle, czy tak ma być i czy można to jakoś uprościć, bo koszmarnie to wygląda

Saizou :

R		a
	=
sin(90−α)		sin(2α)

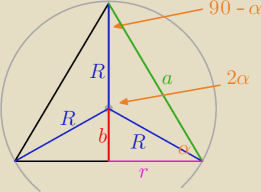
a=2Rsinα

	r
cosα=
	a

r=2Rsinαcosα=R*sin(2α)

	R+b
sinα=
	a

R+b=2Rsin²α b=R(2sin²−1)=R*cos(2α)

	1		1
V=		πR2*sin2(2α)*(R+R*cos(2α))=		πR3*sin2(2α)(1+cos2(2α))
	3		3

salamandra: Hm, jedynie to się u nas różni ja mam na końcu 2sin²α, a ty (1+cos²(2α)), jest to równoważne?

Saizou : Nie, dla kąta np. α=30° się rozjeżdża

salamandra: Spróbuję poszukać błędu, a jak nie, to skorzystam z Twojego sposobu, dzięki

salamandra: Nie widzę u siebie błędu

Saizou : Pokaż swoje rozwiązanie wraz z rysunkiem

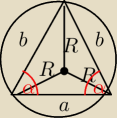
salamandra: b=R*2sinα

	a
R=
	2sin(180−2α)

a=R*2sin(2α)

	H		H
sinα=		=
	b		R*2sinα

H=R*2sin²α Pp=π*(2Rsin2α)²=R²*sin²2α*π Pb=π*Rsin(2α)*R*2sinα*Rπ*4sin(2α)sinα Pc=R²sin²(2α)*π+Rπ*4sin2αsinα = Rπ(Rsin²2a+4sin2a*sinα)

	1		1
V=		*R2*sin2(2α)*π*R2sin2α =		R3π*sin2(2α)*2sin2α
	3		3

Saizou :

	1
U Ciebie r=		a, zatem
	2

	1
Pp=πr2=π*(		*2Rsin(2α))=πR2sin2(2α)
	2

P_b=πrl=π*Rsin(2α)*2Rsinα=2πR²sinα*sin(2α) P_c=πR²sin(2α)(sin(2α)+2sinα) u mnie źle jest pod koniec wyniki mamy takie same, bo 1+cos2x=2sin²x wynika to z równości cos2x=cos²x−sin²x 1=sin²x+cos²x =======+ 1+cos2x=2sin²x

salamandra: Czyli oboje mamy źle?

Saizou : Objętość mamy dobrze, tylko ja źle wklepałem do laptopa

	1
V=		πR3*sin2(2α)(1+cos(2α))=
	3

1
	πR3*sin2(2α)*2sin2α
3

salamandra: Źle przepisałem pole boczne, przepisałem pole całkowite dwa razy. Pc mam dobrze? Bo u Ciebie troche inaczej to wyglada

salamandra:

	1
Pb=π*		α*b
	2

Pb=π*R*sin(2α)*R*2sinα = πR²sin(2α)*sin(α)

	1
Pp=π*(		a)2 = π*R2*sin2(2α) = R2π*sin2(2α)
	2

Pc=R²π*sin²(2α)+πR²sin(2α)*sin(α) = πR²(sin²(2α)+2sin(2α)*sin(α))= πR²*sin(2α)(sin(2α)+2sin(α)) Nie wiem skąd wytrzasnąłem to 4sin2a wcześniej, dzieki wielkie Saizou

Saizou : na zdrowie