 W stożku obrotowym kąt nachylenia tworzącej do płaszczyzny podstawy ma miarę \alpha. Na stożku
opisano kulę o promieniu R.
Oblicz objętość i pole powierzchni całkowitej tego stożka.
Nie potrafie rysować na tej stronie >.< Narysowałem to tak :
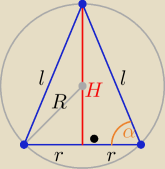
R − promień kuli
H − Wysokosc stożka ===> H = R+x
r − promien podstawy
l − tworząca stożka
α − kąt miedzy tworzącą a podstawą.
Następnie ułożyłem taki układ równań
x2 + r2 = R2
(R+x)2 + r2 = l2
W stożku obrotowym kąt nachylenia tworzącej do płaszczyzny podstawy ma miarę \alpha. Na stożku
opisano kulę o promieniu R.
Oblicz objętość i pole powierzchni całkowitej tego stożka.
Nie potrafie rysować na tej stronie >.< Narysowałem to tak :
R − promień kuli
H − Wysokosc stożka ===> H = R+x
r − promien podstawy
l − tworząca stożka
α − kąt miedzy tworzącą a podstawą.
Następnie ułożyłem taki układ równań
x2 + r2 = R2
(R+x)2 + r2 = l2
| r | ||
cosα = | ||
| l |

| l | ||
Z tw. sinusów | =2R ⇒ l=2Rsinα | |
| sinα |
| r | |
= cosα ⇒r=l*cosα ⇒r= 2Rsinα*cosα ⇒r = Rsin(2α) | |
| l |
| H | |
= sinα ⇒ H=l*sinα ⇒ H= 2Rsin2α | |
| l |
 Nie powiem ale moim sposobem sie sporo naliczyłem
Nie powiem ale moim sposobem sie sporo naliczyłem  Dziękuje
Dziękuje 
