Równania prostych Marcin21: Punkty A= (2,0), B=(8,2), C=(6,−4) są wierzchołkami trójkąta, Wyznacz równanie prostej, w której zawarta jest wysokość CD tego trójkąta oraz oblicz długość środkowej AE.

Jerzy: Zacznij od równania prostej AB

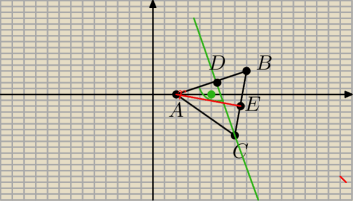
a7: 1. robimy rysunek 2. wyznaczamy prostą prostopadłą do prostej AB przechodzącą przez punkt C 3. wyznaczamy środek odcinka BC i liczymy długość odcinka AE 2. prosta protopadła do AB prosta AB ma równanie y=ax+b

	1
k{0=2a+b & 2=8a+b stąd a=		b=2/3
	3

prosta CD ma równanie y=−3x+b i przechodzi przez punkt C −4=−18+b b= 14 3. punkt E ma współrzędne E(7,−1) https://matematykaszkolna.pl/strona/1750.html długość odcinka AE wynosi √26 https://matematykaszkolna.pl/strona/1248.html

Jerzy: A po co rysunek ?

a7: nie każdy widzi co ma policzyć bez rysunku

Jerzy: Czy napisanie równania prostej przechodzącej przez dwa punkty wymaga rysunku ?

6latek: Ja jestem za rysunkiem (nawet najprostszym) Chyba ze w tresci zaznaczono( bez rysunku)