Proszę o pomoc w rozwiazaniu zadania Sebastian Porowski: Cześć Proszę o pomoc w rozwiązaniu zadania zadanie numer 1 https://zapodaj.net/f44b82b757f07.jpg.html Otrzymałem poradę odnośnie tego zadania w poście https://matematykaszkolna.pl/forum/381180.html jednak nie wiem jak się za to zabrać

6latek: |q|<1 ⇔q<1 i q>−1

ICSP: |q| < 1 ⇒ (q−1)(q+1) < 0

ICSP: |a/b| < 1 ⇒ (a−b)(a+b) < 0 gdy b ≠ 0

Sebastian Porowski: Można prosić o wytłumaczenie?

Sebastian Porowski: Ponawiam prośbę ,poniewaz nie wiem skąd to sie bierze

SEBASTIAN POROWSKI: Podbijam

ICSP: https://matematykaszkolna.pl/strona/297.html

Mila:

	x−1
a1=1, a2=		,
	2x−3

	3
2x−3≠0⇔x≠
	2

	a		x−1
q=		=
	a1		2x−3

	x−1
|		|<1 szereg zbieżny
	2x−3

	x−1
−1<		<1
	2x−3

x−1		x−1
	>−1 i		<1
2x−3		2x−3

x−1		x−1		3
	+1>0 i		−1<0 i x≠
2x−3		2x−3		2

x−1		2x−3		x−1		2x−3
	+		>0 i		−		<0
2x−3		2x−3		2x−3		2x−3

x−1+2x−3		x−1−2x+3
	>0 i		<0
2x−3		2x−3

3x−4		−x+2
	>0 i		<0⇔
2x−3		2x−3

(3x−4)*(2x−3)>0 i (−x+2)*(2x−3)<0

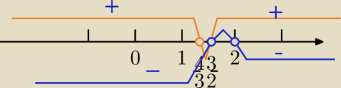
	4		3		3
x=		,x=		, x=2, x=
	3		2		2

	4		3		3
(x<		lub x>		) i (x<		lub x>2) część wspólna
	3		2		2

odp.

	4
x<		lub x>2
	3

==================

Sebastian Porowski: Mam pytanie odswieżam sobie wiedze przed poprawami i chciałbym się dowiedzieć skąd sie bierze

	x−1
stwierdzenie ,że |		|<1 jest szeregiem zbieżnym?
	2x−3