tryg Karol: Wyznacz zbiór wartości funkcji a)y = sinx + cosx

	π		π
b) y = sin(x−		) + sin(x+		)
	6		6

Nie mam pojęcia jak zabrac się za to zadanie, proszę o jakieś wskazówki

the foxi: 3670

the foxi: 3670 ← tu poprawny link

Janek191:

	π
a) y = sin x + cos x = √2 sin (		+ x)
	4

więc ZW = < −√2 , √2 >

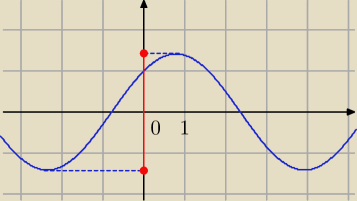
Janek191: b) Zastosuj wzór na sumę sinusów Wykres do a)

Karol:

	π
w b) wyszło mi 2sinx*cos		i nie wiem co dalej
	12

Karol: już jasne, wiem gdzie robiłem bład

Karol: jednak jeszcze potrzebuję pomocy

	π
mam 2sinx*cos		jak z tego dojść do rozwiązania <−√3,√3>?
	6

the foxi:

	π		√3
cos		=
	6		2

	π		√3
2sinx*cos		=2sinx*		=√3sinx
	6		2

Krzysiek60:

	√3
cos30o=
	2

karol:

	√3
y=2sinx*		= √3sinx Zw=<−√3, √3>
	2

Karol: jak interpretować ten "x" przy sin? bo z tym mam problem

Krzysiek60: Funkcja y=sin jako taka nie istnieje Musi posiadac argument .Tym argumentem jest (x) y= sin(x)

Karol: dobra, dzięki