3 zadanka z czworokatow liceum tomek3: 1. dany jest trojkat opisany na okregu, jego przekatna = 7cm, promien = 3cm oblicz pole, obwod i srodkowa trapezu 2.dany jest romb, ktorego a+h, czyli suma boku i wysokosci na ktory pada wynosi 10cm. cosinus kąta ostrego w rombie wynosi 4/5. oblicz pole, obwod i przekatne rombu 3. udowodnij, ze dluzszą przekątną deltoidu jest średnica okręgu w który jest wpisany.

tomek3: 1. dany jest trapez*

a7: zad3. https://matematykaszkolna.pl/forum/243633.html

tomek3: @a7 A skąd @Eta mogła założyć, że dane kąty to 30,60,90 stopni?

a7: nie wczytałam się, ale zaraz spróbuję spojrzeć

a7: wiemy " z góry", że "Na czworokącie można opisać okrąg wtedy i tylko wtedy, gdy sumy miar jego przeciwległych kątów wewnętrznych są równe 180°": (https://matematykaszkolna.pl/strona/wzoryMatura2015.pdf) oraz wiadomo, że deltoid to taki czworokąt który ma oś symetrii

a7: przekątne deltoidu przecinają się pod kątami prostymi to też na pewno

a7: gdyby dłuższa przekątna nie była jednocześnie średnicą to deltoid nie miałby osi symetrii, może o to chodzi?

a7: jeśli chodzi rozwiązanie @Ety to wzięła ona chyba pod uwagę jeden z przypadków, ale może się odezwie to będzie wiadomo

a7: jeżeli weźmiemy dowolny odcinek przecinający okrąg i ten odcinek ma być przekątną deltoidu to aby miał ten deltoid oś symetrii to albo musimy wziąć na początku srednicę albo drugi z "dorysowywanych" odcinków (pod kątem prostym do pierwszego) musi być średnicą inaczej nie byłoby osi symetrii tego deltoidu oś symetrii deltoidu przechodzi przez jego wierzchołki, ale to rozumiem, że było dorozumiane https://pl.wikipedia.org/wiki/Deltoid czy teraz już się wyjaśniło?

tomek3: @a7 tak średnio... a nie dałoby się to w jakiś inny sposób udowodnić?

a7: pewnie się da, ja dorzuciłam swoje trzy grosze na chłopski rozum, tu jeszcze jeden link https://matematykaszkolna.pl/forum/361146.html w którym @Alky wyjaśnił zrozumialej że ponieważ mamy tam dwa kąty proste (tego deltoidu) to przeciległa musi być średnicą, bo kąty mają 90 stopni, a pary boków deltoidu są równe (z definicji), więc musi to być średnica − os symetrii teraz lepiej?

tomek3: @a7 chodzi ci o to, że jeżeli jest przekątna deltoidu dotykająca w dwóch punktach okrąg, to albo jest ona średnicą, albo średnicą jest odcinek przecinający ją pod kątem prostym (druga przekątna deltoidu) tak? ale skoro tak, to jak wykluczyć możliwość, że to właśnie ten odcinek (2 przekątna) jest średnicą, a nie ta pierwsza przekątna?

tomek3: post napisany przed twoim postem z 23:39 czyli wystarczy napisać, że jest kąt prosty Beta ( bo skoro na deltoidzie opisano okrąg, to 2B=180s a więc B = kąt prosty) w trójkącie prostokątnym, którego przeciwprostokątna zawsze wynosi 2r (średnica) i zadanie full pkt?

a7: trzeba napisać, zę "Na czworokącie można opisać okrąg wtedy i tylko wtedy, gdy sumy miar jego przeciwległych kątów wewnętrznych są równe 180°": (https://matematykaszkolna.pl/strona/wzoryMatura2015.pdf) oraz wiadomo, że deltoid to taki czworokąt który ma oś symetrii oraz pary sa siadujących boków równe, tylko wtedy da się więc wpisać w okrąg deltoid, gdy jedna z jego przekotnych to średnica okręgu, gdyż ta przekątna jest bokiem wspólnym trójkątów przystakjących z których jest deltoid a te trójkaty są prostokątne, więc ich kąty proste musża musza być oparte na srednicy okręgu ale nie wiem czy to full pktów

a7: jest to logiczne i wynika jedno zs drugiego jeszcze powinien byc rysunek koniecznie

a7: trójkąty są przystające bo deltoid ma oś symetrii, to było ale na wszelki wypadek można tam dodać drugi raz

tomek3: a nie mozna nazwac ten deltoid ABCD i przeciecie przekatnych to S i wtedy napisac, ze Deltoid ABCD jest opisany na okregu, wiec suma każdej z par jego przeciwleglych katow = 180 stopni stąd wynika, że Beta + Beta = 180 stopni, czyli Beta = 90 stopni Stąd wynika, że trókąt ABC jest trójkątem prostokątnym opisanym na okręgu, którego przeciwprostokątna, która jest także dłuższą przekątną deltoidu ABCD, musi być równa dwóm promienion, czyli średnicy okręgu. Tak też jest dobrze? i rysunek taki http://scr.hu/0e4f1/2rs15

a7: tak mi się wydaje, że to się trzyma kupy, tu jeszcze rysunek @Alky'ego z linku https://matematykaszkolna.pl/forum/361146.html https://matematykaszkolna.pl/forum/rysunek134813.png

a7: tylko pisząc że jest równy dwóm promieniom czyli średnicy sugerujesz, że promienie miały tu coś wspólnego z Twoim wywodem to bym pomineła (o tych peominiach) zostawiła o samej średnicy

a7: i jeszcze jest trójkątem prostokatnym wpisanym! w okrąg

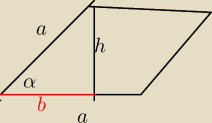
a7: Zad2. cosα=b/a=4/5 a+h=10 a=10−h obliczamy sinα z jedynki trygonometrycznej sinα= 3/5 obliczamy a sinα=h/a=3/5 a=5h/3 a=10−h h=15/4 a= 25/4 Obliczamy Pole i Obwód P=1/2ah = 1/2a²sinα Obw=4a

a7: przepraszam pomyłka we wzorach na P rombu P=ah=a²sinα

tomek3: dzieki. z przekatnymi sobie dalej poradze