k Barry: Ponawiam prośbę o zrobienie zadania Deltoid ABCD jest wpisany w okrąg. Udowodnij, że dłuższa przekątna deltoidu jest średnicą okręgu.

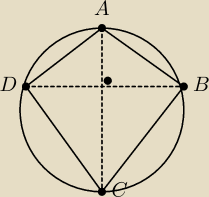
Wazyl: Kąt między przekątnymi jest prosty co oznacza że dłuższa przekątna jest przeciwprostokątną ΔABC.

Wazyl: Bzdury napisałem. Pospieszyłem się

PW: Deltoid jest tworem symetrycznym względem prostej zawierającej dłuższą przekątną BD (to wiemy skądinąd). W tej symetrii jeden koniec krótszej przekątnej zamienia się miejscami z drugim końcem, nazwijmy je A i C. Mamy więc S_BD(A) = C i S_BD(C) = A. Punkty A i C należą również do okręgu. Oznacza to, że na okręgu są dwa punkty symetryczne nawzajem w symetrii S_BD. Tym samym prosta BD jest osią symetrii okręgu, a więc odcinek BD jest średnicą (każda oś symetrii okręgu zawiera średnicę okręgu)

PW: Szkoda że nie widziałem rysunku Wazyla, przyjąłbym jego oznaczenia.

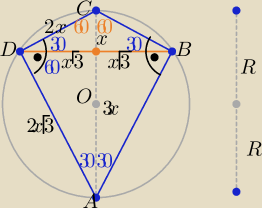
Eta: Ze związków miarowych w trójkątach "ekierkach" o kątach 30^o,60^o,90^o x>0, |DB|=2x√3 , |AC|=4x

	|DB|*|AC|		2x√3*4x
2R=4x P=		=		=8√3 ⇒ x2=2 ⇒ x=√2
	2		2

to: 2R=........ ⇒R=...... dokończ

Eta: https://matematykaszkolna.pl/forum/243630.html Echh nie w tym poście napisałam

Barry: Wielkie dzięki