zadanie
johnik: Rozważmy okrąg o równaniu (x−3)2 + (y+2)2 = 36. Poza kołem wyznaczonym przez okrąg wybieramy
punkt P=(10, 3). Prowadzimy proste, które przechodzą przez punkt P i przecinają dany okrąg w
dwóch punktach. Jaką figurę tworzy zbiór środków wyznaczonych cięciw?
Czy takie zadanko moze sie trafic na maturce

czy juz przesada

Bardzo prosze o pomoc bo
kosmiczne literki mam

2 cze 17:22
): pytanko o to zadanko, to do CKE, drogi johniku
2 cze 17:29
): we wtoreczek będzie wiadomo, obie maturki jednego dnia
2 cze 17:30
johnik: to w takim razie ma ktoś propozycje rozwiazania

2 cze 17:33
): to pisz od razu, że chcesz żeby ktoś to za ciebie zrobił
po co piszesz o przesadzie
2 cze 17:37
a7: no szkicujemy i wychodzi jakiś łuk z tych środków, nie?
2 cze 17:38
2 cze 17:54
2 cze 18:18
johnik: to w takim razie na czym polega roznica w odpowiedzi na przykladach z zadania.info

2 cze 19:34
a7: to znaczy tam mamy okrąg o srodku w inym punkcie, punkt P jest gdzie indziej umieszczony, więc
obliczenia będą odpowiednio inne,
zrób może rysunek i zobaczysz. Twój okrąg ma srodek w punkcie (3,−2) a promień 6
2 cze 19:48
a7: W Twoim zadaniu zresztą jest pytanie jaka to figura jest z tych środków cięciw, więc odpowiedź
to: łuk
2 cze 19:51
Mila:
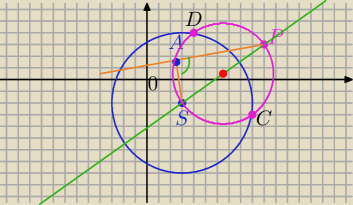
O1: (x−3)
2 + (y+2)
2 = 36, P=(10, 3).
Prowadzę prostą przechodzącą przez punkty P i początek układu współrzędnych i prosta PS
A(x,y)− środek cięciwy⇒SA⊥AP
|PS|
2=7
2+5
2=49+25=74
Z tw. Pitagorasa:
|AP|
2+|AS|
=|PS|
2
(10−x)
2+(3−y)
2+(3−x)
2+(−2−y)
2=74⇔
| | 13 | | 1 | | 74 | |
(x− |
| )2+(y− |
| )2= |
| |
| | 2 | | 2 | | 4 | |
Mamy łuk CSAD wewnątrz okręgu O1.
Teraz tylko ograniczenie dopisz.
2 cze 22:01
johnik: dziekuje

3 cze 00:08
 czy juz przesada
czy juz przesada Bardzo prosze o pomoc bo
kosmiczne literki mam
Bardzo prosze o pomoc bo
kosmiczne literki mam 


 O1: (x−3)2 + (y+2)2 = 36, P=(10, 3).
Prowadzę prostą przechodzącą przez punkty P i początek układu współrzędnych i prosta PS
A(x,y)− środek cięciwy⇒SA⊥AP
|PS|2=72+52=49+25=74
Z tw. Pitagorasa:
|AP|2+|AS|=|PS|2
(10−x)2+(3−y)2+(3−x)2+(−2−y)2=74⇔
O1: (x−3)2 + (y+2)2 = 36, P=(10, 3).
Prowadzę prostą przechodzącą przez punkty P i początek układu współrzędnych i prosta PS
A(x,y)− środek cięciwy⇒SA⊥AP
|PS|2=72+52=49+25=74
Z tw. Pitagorasa:
|AP|2+|AS|=|PS|2
(10−x)2+(3−y)2+(3−x)2+(−2−y)2=74⇔
