Geometria Overplay: Znajdź zbiór środków wszystkich cięciw okręgu x² + y² + 4y +3=0, wyznaczonych przez proste przechodzące przez P(0,1).

Overplay: ?

Overplay: ma ktos pomysl?

Overplay: prosze o pomoc

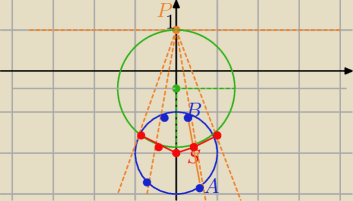
Eta: Środki tych cięciw leżą na części okręgu

	1		9
o: x2+y2+y−2=0 = x2+(y+		)2=
	2		4

Overplay: a ten okrag "zielony" nie powinien miec srodek w pkt P i promien dlugosci 3?

Mila: http://www.zadania.info/7862894 Tam masz rysunki i obliczenia.

Eta:

Overplay: Kurcze, wogole jakoś nie moge tego zrozumieć

Mila: Kąt OSB=90⁰ bo OS to odcinek łączący środek okręgu (niebieskiego) ze środkiem cięciwy AB, w takim razie kat OSP=90⁰ to znaczy ,że jest kątem wpisanym w okrąg opartym na średnicy OP.

	1		1
Srodek tego okręgu to punkt (0;−		) i r=		|OP|
	2		2

Równanie tego okręgu:

	1		9
x2+(y+		)2=		po rozwinięciu
	2		4

x²+y²+y−2=0 Znajdź punkty przecięcia okręgów: x²+y²+y−2=0 i x² + y² + 4y +3=0 aby określić zakres punktów z tego zielonego okręgu, które są środkami cięciw.