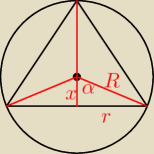
błąd Basia: Pomóżcie mi znaleźć błąd Rozwiażamy stożki wpisane w kulę o danym promieniu R i kącie rozwiarcia (0,90>. Szukamy stożka o największej objętości. Wydaje mi się, że maksimum osiągniemy dla α=60, ale.................

	r
sin α =
	R

	x
cos α =
	R

te równania są prawdziwe także dla α=90 r = R*sin α x = R*cos α h = R+x = R(1+cos α)

	1		1
V =		πr2*h =		π*R3*sin2(α)*(1+cosα)
	3		3

	1
V' =		πR3*[2sin(α)*cos(α)*(1+cos α) + sin2(α)*(−sin α]
	3

	1
V' =		πR3*(sin α)*[2(cos α)(1+cos α) − sin2 α]
	3

	1
V' =		πR3*(sinα)*[2cos α + 2cos2 α −1 + cos2 α]
	3

	1
V' =		πR3*(sin α)*(3cos2 α + 2cos α −1)
	3

1
	πR3*(sin α) >0 dla każdego α∊(0;90>
3

V'=0 3cos² α + 2cos α −1=0 t = cos α t∊<0; 1) 3t²+2t−1=0 (3t−1)(t+1)=0

	1
t =		lub t=−1
	3

	1
t∊<0;		) ⇒ V'<0 ⇒V maleje
	3

	1
t∊(		;1) ⇒ V'>0 ⇒ V rośnie
	3

wynikałoby z tego, że V_max osiągamy dla t=0 czyli dla α=90 a to jest nieprawda

	1
dla α =90 V=		πR3
	3

natomiast dla α=60 (czyli dla stożka, którego przekrój jest trójkątem równobocznym mamy

	2
R =		h
	3

	3
h =		R
	2

	a√3
h =
	2

	2h		3   2* R   2
a =		=		= U{3R}{√3 = R√3
	√3		√3

	R√3
r =
	2

	1		3R2		3		1		9		1
V =		π*		*		R =		πR3*		>		πR3
	3		4		2		3		8		3

co tu do diabła jest źle; wrrrrrrrrr...............

Adamm: 60 − liczba 60 60^o − kąt 60 stopni

jc: Coś podobnego: https://matematykaszkolna.pl/forum/323757.html

Basia: stopnie miały być oczywiście, ale gdzieś poginęły

Basia: jc ja wiem jak to wykazać i nie o to mi chodzi chodzi mi o to dlaczego z rachunku pochodnych głupoty tutaj wychodzą

Adamm: to z tymi cosinusami od razu bym pominął t=cosα≥0 już na początku V=−c*(t²−1)(t+1), c>0 V=−c*(t−1)(t+1)² V'=−c*[(t+1)²+2(t+1)(t−1)]=−c*(t+1)(3t−1) mamy minimum dla t=−1, mamy maksimum dla t=1/3 czyli maksimum dla cosα=1/3

	25
V=		πR3
	34

Adamm: czyli już wiadomo o co chodzi, gdzieś była zmiana znaku, maksima pomyliły ci się z minimami

Basia: gdzieś znak się nie zgadza u mnie V byłoby tak jak u Ciebie V = c(1−t²)(1+t) ale w V' nie wyszedł mi ten minus gdy liczę bezposrednio z trygonometrycznych bo wyszło V' = c(3t−1)(t+1) gdzieś musi być błąd, ale nie umiem go znaleźć rzuć Adamm okiem może znajdziesz, bo pewnie czymś się zasugerowałam i nie umiem się "odkleić" a znalezienie tego błędu jest mi koniecznie potzrebne

jc: t = cos a Różniczkujesz złożenie. t' = − sin a < 0 w rozpatrywanym przedziale.

Basia: Nie podstawiam, różniczkuję bez podstawienia i tam chcę znaleźć błąd

Basia: Panowie, wiem, że macie dobre pomysły na podstawienie i uproszczenie obliczeń, ale ja muszę znaleźć błąd, w tym konkretnym, przepisanym przez mnie, rozwiązaniu. A nie widzę go.

jc: Dlaczego tak bardzo zależy Ci na znalezieniu błędu? Zrozumiałbym to tylko w przypadku poszukiwania błędu w nieswojej pracy. Sam wolałbym poszukać lepszego rozwiązania. (3t−1)(t+1) Przedział po lewej stronie to [1/3,1), a po prawej masz [0,1/3] Po prostu t=cos a maleje od 1 do 0. Dlatego najpierw funkcja rośnie, a potem maleje.

jc: Dla małych a, t jest duże i pochodna jest dodatnia (funkcja rośnie). Dla dużych a, t jest małe i pochodna jest ujemna (funkcja maleje). Po drodze masz więc maksimum.

Basia: Bo to właśnie nie jest moje rozwiązanie. I muszę wytłumaczyć autorowi dlaczego ono nie jest poprawne. Gdyby autor różniczkował po podstawieniu powiedziałabym, że zapomniał o zróżniczkowaniu funkcji wewnętrznej, ale on to podstawienie robi dopiero po zróżniczkowaniu. Więc jak wytłumaczyć, że podstawieniu t=cosx już po policzeniu pochodnej i uzyskaniu funkcji f(t) = 3t²+2t−1 nie dostajemy poprawnego wyniku? Owszem y=cos x jest malejąca, natomiast y=t jest rosnąca

	1
więc teoretycznie powinno się podstawić		= cosx
	t

Wtedy będzie dobrze

3		2		3+2t−t2
	+		−1 =		i wszystko "zagra"
t2		t		t2

Tylko autor zapyta mnie natychmiast dlaczego bez żadnych "takich" podstawiam sobie t=x² w równaniu dwukwadratowym (2n,n,0). Przecież y=x² też nie jest rosnąca dla x<0, a t jak najbardziej.

Basia: (4,2,0) miałam na myśli; np. x⁴−5x²+1

Pytający: α∊(0;π/2> t=cos(α) Wtedy: t∊<0;1/3) ∧ V'<0 ⇒ cos(α)∊<0;1/3) ⇒ α∊(arccos(1/3);π/2> // i wtedy V maleje t∊(1/3;1) ∧ V'>0 ⇒ cos(α)∊(1/3;1) ⇒ α∊(0;arccos(1/3)) // i wtedy V rośnie Swoją drogą czy "kąt rozwarcia" jest poprawnie zaznaczony na rysunku, Basiu? (1003)

Basia: Wiem jak to wytłumaczyć; w równaniach i nierównościach możemy tak sobie podstawiać, bo interesuje nas tylko znak. Natomiast tam gdzie dalej chcemy badać monotonicznoć nie bardzo możemy podstawić rosnącą za malejącą (lub odwotnie). A najlepiej podstawiać przed różniczkowaniem i nie zapominać o funkcji wewnętrznej.

Basia: Adamm źle napisałam: kąt przy wierzchołku przekroju osiowego miał być oczywiście

Basia: ale to to samo zasugerowałeś się kątem α z rysunku Jakuba ? γ to kąt rozwarcia na tym rysunku u mnie nie zaznaczony no ale jak wpisany α, to środkowy 2α; połowa środkowego α

Pytający: Tak, spojrzałem na rysunek i "przecież co innego jest zaznaczone". Ale już widzę, że to jedno i to samo w tym przypadku. A formalnie chyba coś w tym stylu trzeba by zrobić (zapis może nie być poprawny, różniczki nie były i raczej nie będą moją mocną stroną):

	ϱV
V'(α)=		=D
	ϱα

t=cos(α) ⇒ α=arccos(t)

	ϱV		ϱV		ϱα		−1
V'(t)=		=		*		=D*
	ϱt		ϱα		ϱt		√1−x2

Basia: Najlepsze jest podstawienie od razu na poczatku, tak jak zaproponował Adamm. Upierałam się nie przy sposobie rozwiązania, ale przy wyjaśnieniu dlaczego "jest źle". Zrozumienie jak i dlaczego popełniło się błąd jest bardzo cenne i potem procentuje. Dziękuję wszystkim za pomoc

Iryt:

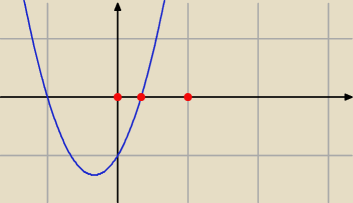
PW: To samo co Pytający o 14:57, bardziej szkolnym językiem. To jest wykres g(t)=(3t−1)(t+1), ale przecież założyliśmy t∊(0, 1), więc mamy:

	1
− dla t∊(0,		) pochodna jest ujemna
	3

	1
− dla t∊(		, 1) pochodna jest dodatnia.
	3

Jednak t to nie x, zdania powyżej trzeba przetłumaczyć "na język x". Tu warto pokazać na wykresie kosinusa):

	1		π
− jeżelicosx∊(0,		), to pochodna jest ujemna (tzn. dla x∊(α0,		))
	3		2

	1
− jeżeli cosx∊(		, 1) pochodna jest dodatnia (tzn. dla x∊(0,α0)),
	3

	1
gdzie α0 oznacza kąt, dla którego cosα0=		.
	3

Maksimum dla x=α₀ (około 70,5°).

Basia: Dziękuję PW Dobre wytłumaczenie "szkolnym" językiem. To mi było potrzebne