Wyznaczenie przecięcia prostej l z osią OX/OY Aeshon:

	⎧	x=7t+9
Dana jest prosta l:	⎩	y=−9t−2	t∊ℛ

Muszę wyznaczyć z niej punkty przecięcia z osią OX/OY. Zacząłem od wyznaczenia parametru T, ale ewidentnie coś tu pokręciłem.

⎧	−7t=9−x/:(−7)
⎩	9t=−2−y/:(9)

⎧	t=−(9/7)+(1/7)x
⎩	t=−(2/9)+(1/9)y

Mógłby ktoś pokierować gdzie popełniam błąd?

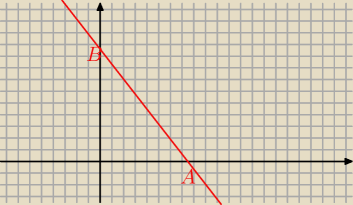
Janek191: 9 x = 63 t + 81 7 y = − 63 t − 14 −−−−−−−−−−−−−−−−−− 9x + 7 y = 67 Z osia OX y = 0 9 x = 67

	67
x =
	9

	67
A = (		, 0)
	9

Z osią OY x = 0 7 y = 67

	67
y =
	7

	67
B = ( 0 ,		)
	7

Aeshon: Bardzo dziękuję

Pytający: Aeshon, jedyny błąd masz w ostatniej linijce, powinno być: t=−(2/9)−(1/9)y Punkt przecięcia z OX mógłbyś tak obliczyć: y=0 ⇒ t=−(2/9)−(1/9)*0=−2/9 ⇒ x=7*(−2/9)+9=67/9

Aeshon: Okazało się, że muszę jeszcze z tego wyznaczyć jakiś wektor normalny(?). Tutaj znalazłem 1214,że można go łatwo wyznaczyć z postaci ogólnej prostej. Tylko jak należy przekształcić do tej postaci z tego układu równań?

Aeshon: @edit Złe cyfry wpisałem w odnośniku. Miałem na myśli to https://matematykaszkolna.pl/strona/1214.html

Aeshon: Już mi się udało zrobić. Jeszcze raz dzięki za pomoc.

Pytający: Tak jak Janek napisał: 9x + 7 y = 67 Czyli postać ogólna to: 9x+7y−67=0