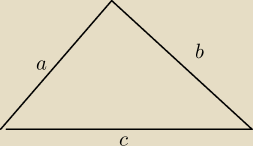
Boki trojkąta
Powracający: Udowodnij ze jesli a, b, c sa dlugosciami bokow trojkata to
17 wrz 00:09
bezendu:
a2+b2>1/2c2 /2
2a2+2b2−2c2>0
a2+2ab+b2−2c2−2ab>0
(a+b)2−2(c+2ab)>0
Wystarczy napisać dobry komentarz teraz.
17 wrz 00:13
Adamm: c2=a2+b2−2ab*cosα
2a2+2b2−c2=a2−2ab*cosα+b2=(a−b)2+2ab(1−cosα)>0
17 wrz 00:13
bezendu:
Sorry, nie doczytałem całego. Nie patrz na mój post.
17 wrz 00:13
17 wrz 00:15
Powracający:
Przepraszam ale zaczytalem sie .
Adamm zrobiles to z tw cosinusow
Ale jezeli chcielibysmy zrobic tak jak zaczal
bezendu to
c<a+b ⇔
c
2<a
2+b
2+2ab
Teraz jak oszacowac ten skladnik 2ab?
i czy nam to cos da zebysmy dostali teze ?
17 wrz 00:25
Adamm: nie wiem
17 wrz 00:36
Powracający: OK.
17 wrz 00:40
17 wrz 00:42
Eta:
Można też tak:
Z nierówności trójkąta
a+b>c /2
a2+2ab+b2>c2 i (a−b)2>0
a2−2ab+b2>0
+ −−−−−−−−−−−−−−−−
2a2+2b2>c2 /:2
a2+b2>c2/2
c.n.w.
17 wrz 00:54
Powracający: dzieki Eta .
17 wrz 00:57
Eta:

17 wrz 00:58
 Przepraszam ale zaczytalem sie .
Adamm zrobiles to z tw cosinusow
Ale jezeli chcielibysmy zrobic tak jak zaczal bezendu to
c<a+b ⇔
c2<a2+b2+2ab
Teraz jak oszacowac ten skladnik 2ab?
i czy nam to cos da zebysmy dostali teze ?
Przepraszam ale zaczytalem sie .
Adamm zrobiles to z tw cosinusow
Ale jezeli chcielibysmy zrobic tak jak zaczal bezendu to
c<a+b ⇔
c2<a2+b2+2ab
Teraz jak oszacowac ten skladnik 2ab?
i czy nam to cos da zebysmy dostali teze ?
