da J: Ma ktoś jakieś zadanie żeby pocwiczyc twierdzenie Stewarta?

Rafal: Najlepiej nie zaśmiecaj sobie nim umysłu. Można je bez problemu wyprowadzić, pisząc dwa twierdzenia cosinusów.

J: a twierdzenie cevy? Chyba przydatne

Rafal: Ostatnio ktoś wrzucił geometrię z tegorocznej matury próbnej z operonu (chyba), które da się zrobić tym twierdzeniem i to bardzo szybko. Dany jest trapez ABCD. Punkt E jest punktem przecięcia się przekątnych. Ramiona przedłużono do przecięcia w punkcie F. Wykaż, że prosta EF dzieli dłuższą podstawę trapezu na połowy.

J: Ale o którym twierdzeniu mówisz?

Rafal: Twierdzenie Leonarda Cevy, rzecz jasna To twierdzenie podchodzi pod tematykę olimpijską, więc nie wiem, czy będziesz zainteresowany zadaniami z nim związanymi. Jeśli tak, to pisz.

J: I jak zrobić to zadanie z operonu bo nie widze tego

Rafal: Najpierw twierdzenie Talesa

AiO: Do tw Cevy nalezaloby dolaczyc tez Tw Menelaosa . Ale to tez tematyka olimpijska raczej

J: Prawda, ciężkie i chyba jednak mi nie potrzebne

Rafal: I jak poszło zadanko?

J: nie zrobiłem

Rafal:

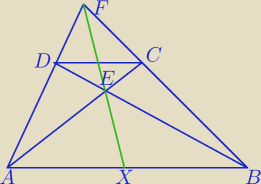
	FC		FD
Z twierdzenia Talesa		=		.
	CB		DA

	AX		BC		FD
Z twierdzenia Cevy		*		*		=1.
	XB		CF		DA

Łącząc te dwie równości, otrzymujemy tezę.

Rafal: Tu ładne rozwiązanie Ety https://matematykaszkolna.pl/forum/353218.html

Adamm: źle

AiO: Masz jedno życie a tak nim szafujesz (pewnie sie podszywasz Pani Eta prawie nigdy sie nie myli

Kacper: Jak ktoś bardzo chce zadania z tw. Menelaosa i Cevy to mam gdzieś książkę geometria trójkąta Zetela.

Rafal: Na mnie już za późno

AiO: Kacper to rarytas Na allegro wola ponad 160zl

Adamm: prawie nigdy, ale się myli nie mówię że pomyłka, bo to nie byłem ja

AiO: Dlatego napisalem ze ktos sie podszywa .

AiO: Kacper . Mam ja w pdf . Jak bedzie tansza to ja kupie .

Rafal: J, masz Twoje twierdzenie Stewarta! https://matematykaszkolna.pl/forum/353322.html