Co tu jest nie tak? Martin: Dany jest trapez ABCD. Punkt E jest punktem przecięcia się przekątnych. Ramiona przedłużono do przecięcia w punkcie F. Wykaż, że prosta EF dzieli dłuższą przekątną trapezu na połowy. Czy odpowiedź, bazująca na tym, żeby dorysować symetryczny trójkąt, odbity względem prostej AB, który stworzyłby deltoid byłaby uznana? I na podstawie tego, że jedna przekątna deltoidu dzieli się na pół udowodnić założenie? I drugie pytanie, czemu
1000 lim n→∞√4x²+x+1−2x nie będzie równać się 0? Pomnożyłam to, żeby sprowadzić do wzoru skróconego mnożenia przez √4x²+x+1+2x

Rafal: 1) Nie widzi mi się to, mógłbyś narysować? A jeśli chodzi o najszybsze rozwiązanie, to... twierdzenie Talesa+twierdzenie Cevy=koniec dowodu

Martin: Dobra, jak tutaj to rysuję to też tego już nie widzę Z twierdzenia Cevy nigdy nie miałam okazji korzystać, ale poczytam i zobaczę Dziękuję

Kacper: Jest błąd w treści, bo EF dzieli dłuższą podstawę,a nie przekątną

Martin: Prawda, mea culpa

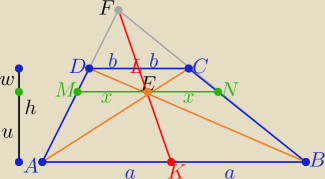
Eta: Dorysuj odcinek MN ∥ AB i przechodzący przez punkt E 1/ z podobieństwa trójkątów ABD i DME oraz ABC i CEN z cechy (kkk)

|ME|		w		|EN|		w
	=		i		=		⇒ |ME|=|EN|=x
|AB|		u		|AB|		u

zatem punkt E jest środkiem odcinka MN i MN∥AB 2/ wniosek z tw. Talesa........... punkty K i L są też środkami podstaw AB i CD co daje tezę