Wzór na dwusieczną. Master: Mógłby mi ktoś pomóc w wyprowadzeniu wzoru na długość dwusiecznej zawartej w trójkącie z wykorzystaniem twierdzeń trygonometrycznych? Wiem, że mam dojść do postaci l= ^{√bc*((b+c)2−a2)}_b+c

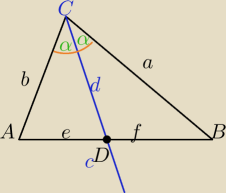
Mila: BC=a, AC=b, AB=c, Długość odcinka dwusiecznej kata zawartej w trójkącie. 1) Z tw. o dwusiecznej kąta wewnętrznego w trójkącie:

b		a
	=		, e+f=a
e		f

	ac		bc
f=		, e=
	a+b		a+b

2) Korzystam z twierdzenia: W każdym trójkącie iloczyn dwóch boków jest równy kwadratowi długości dwusiecznej kąta między nimi zawartego powiększonej o iloczyn odcinków , na które ta dwusieczna podzieliła trzeci bok. ab=d²+e*f

	ac		bc
d2=a*b−		*
	a+b		a+b

	ab*(a+b)2−abc2
d2=
	(a+b)2

	√ab*[(a+b)2−c2]
dc=
	a+b

=================== Analogicznie wyprowadzasz wzór na pozostałe dwusieczne.

Adamm: albo tw. Cosinusów

Master: dziękuje ślicznie

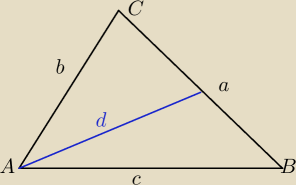
AiO: d− dwusieczna kąta A od wierzcholka A do bolu a

	2bc		A		2		A		p(p−a)
d=		*cos		=		√bcp(p−a) cos		= √
	b+c		2		b+c		2		bc

jest tez taki wzor