Wyznaczanie równania okręgu
KMilan:
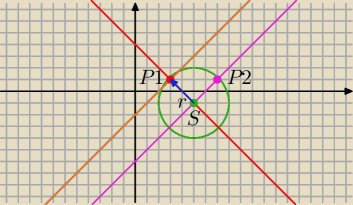
Punkty P1=(3,1) oraz P2=(7,1) należą do okręgu. Styczna do tego okręgu poprowadzona w
w punkcie P1 ma równanie y=x−2. Wyznacz równanie okręgu.
A więc mając punkt
P1 i
P2 wyznaczamy:
1. Wyznaczamy prostą prostopadłą do prostej y=x−2 :
Z warunku prostopadłości przekształcamy a na a
1:
a=1
a
1=−1
Powstaje funkcja y=−x+b do której podstawiamy punkt
P1 potrzebny do wyliczenia
współczynnika b:
1=−3+b
b=4
Mając a
1 i b wyznaczamy wzór prostej prostopadłej do stycznej
y=x−2:
y=−x+4
2. Wyznaczamy prostą równoległą do prostej y=x−2 do której należy punkt P2:
Z warunku równoległości wiemy, że a=a
1
a=1
a
1=1
Powstaje funkcja y=x+b do której podstawiamy punkt
P2 potrzebny do wyliczenia
współczynnika b:
1=7+b
b=−6
Wyznaczamy wzór prostej prostopadłej do stycznej
y=x−2 przechodzącej przez punkt
P2:
y=x−6
3. Mając prostą y=−x+4 i prostą y=x−6 obliczamy punkt ich przecięcia:
2y=−2
y=−1
Podstawiamy y do jednej z prostych, np. do
y=x−6:
−1=x−6
x=5
Mamy x i y, więc środek naszego okręgu ma współrzędne:
S=(5,−1)
4. Z kanonicznej postaci równania okręgu (na stronie
2014)
(x−a)2+(y−b)2=r2
wyznaczamy równanie naszego okręgu wiedząc, że:
S=(5,−1)
r=√8 ← wyliczamy ze wzoru na odległość punktu od prostej (na stronie
1249) używając
punktu
S i prostej
y=x−2
Równanie naszego okręgu ma postać (x−5)2+(y+1)2=8
P.S. To zadanie pojawiło się również tutaj
321166
23 lut 20:52
Adamm: 2. kto ci powiedział że ta prosta przechodzi przez środek okręgu?
23 lut 21:24
Adamm: wyznacz środek okręgu jako punkt na prostej y=−x+4 odległy tak samo od P1 jak i P2
23 lut 21:30
KMilan: Bo styczna jest prostopadła do promienia okręgu.
23 lut 21:48
KMilan: Styczna do okręgu, jest prostopadła do promienia, łączącego punkt styczności ze środkiem
okręgu.
23 lut 21:49
Adamm: to nie sprawia że prosta y=x−6 musi przechodzić przez środek okręgu
gdybyś napisał tak na maturze to z pewnością odjęli by ci punkty
23 lut 21:53
KMilan: Możliwe. To był pierwszy pomysł na to zadanie. Jak możesz, to rozpisz własne rozwiązanie a
komuś na pewno się przyda.
23 lut 21:58
Adamm: mamy jakiś punkt P=(x, −x+4)
P1P=P2P
(x−3)2+(x−3)2=(x−7)2+(x−3)2
|x−3|=|x−7|
x−3=−x+7
x=5
środek okręgu to punkt S=(5, −1)
23 lut 22:04
KMilan:
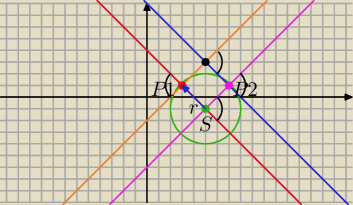
a jeżeli dorysuje prostą prostopadłą do stycznej y=x−2 o równaniu y=−x+8, która z definicji
również jest styczną i uwzględnie ją w rozwiązaniu, to wtedy będzie dobrze?
23 lut 22:36
KMilan: hm?
23 lut 23:12
Eta:
też będzie ok ( ale po co?
24 lut 00:06
 Punkty P1=(3,1) oraz P2=(7,1) należą do okręgu. Styczna do tego okręgu poprowadzona w
w punkcie P1 ma równanie y=x−2. Wyznacz równanie okręgu.
A więc mając punkt P1 i P2 wyznaczamy:
1. Wyznaczamy prostą prostopadłą do prostej y=x−2 :
Z warunku prostopadłości przekształcamy a na a1:
a=1
a1=−1
Powstaje funkcja y=−x+b do której podstawiamy punkt P1 potrzebny do wyliczenia
współczynnika b:
1=−3+b
b=4
Mając a1 i b wyznaczamy wzór prostej prostopadłej do stycznej y=x−2:
y=−x+4
2. Wyznaczamy prostą równoległą do prostej y=x−2 do której należy punkt P2:
Z warunku równoległości wiemy, że a=a1
a=1
a1=1
Powstaje funkcja y=x+b do której podstawiamy punkt P2 potrzebny do wyliczenia
współczynnika b:
1=7+b
b=−6
Wyznaczamy wzór prostej prostopadłej do stycznej y=x−2 przechodzącej przez punkt P2:
y=x−6
3. Mając prostą y=−x+4 i prostą y=x−6 obliczamy punkt ich przecięcia:
Punkty P1=(3,1) oraz P2=(7,1) należą do okręgu. Styczna do tego okręgu poprowadzona w
w punkcie P1 ma równanie y=x−2. Wyznacz równanie okręgu.
A więc mając punkt P1 i P2 wyznaczamy:
1. Wyznaczamy prostą prostopadłą do prostej y=x−2 :
Z warunku prostopadłości przekształcamy a na a1:
a=1
a1=−1
Powstaje funkcja y=−x+b do której podstawiamy punkt P1 potrzebny do wyliczenia
współczynnika b:
1=−3+b
b=4
Mając a1 i b wyznaczamy wzór prostej prostopadłej do stycznej y=x−2:
y=−x+4
2. Wyznaczamy prostą równoległą do prostej y=x−2 do której należy punkt P2:
Z warunku równoległości wiemy, że a=a1
a=1
a1=1
Powstaje funkcja y=x+b do której podstawiamy punkt P2 potrzebny do wyliczenia
współczynnika b:
1=7+b
b=−6
Wyznaczamy wzór prostej prostopadłej do stycznej y=x−2 przechodzącej przez punkt P2:
y=x−6
3. Mając prostą y=−x+4 i prostą y=x−6 obliczamy punkt ich przecięcia:
 a jeżeli dorysuje prostą prostopadłą do stycznej y=x−2 o równaniu y=−x+8, która z definicji
również jest styczną i uwzględnie ją w rozwiązaniu, to wtedy będzie dobrze?
a jeżeli dorysuje prostą prostopadłą do stycznej y=x−2 o równaniu y=−x+8, która z definicji
również jest styczną i uwzględnie ją w rozwiązaniu, to wtedy będzie dobrze?