Geometria- konkursy licealne
Pełcio: Znowu ja..

To są pewnie dość proste zadania, ale z geometrii mi idzie zdecydowanie najsłabiej...
1. W trapezie ABCD (AB||CD) przekątne AC i BD przecinają się w punkcie O takim, że
AO : OC=k (k>1). Pole trójkąta AOD=P. Wyznacz w zależności od P i k pole trapezu.
2. W trójkącie prostokątnym o przeciwprostokątnej AB, wybrano punkt S, dla którego trójkąty
SAB, SBC i SAC mają równe pola. Wiedząc, że SA
2+SB
2=5, oblicz SC.
3. W prostokącie ABCD dane są długości boków AB=5 i AD=2. Na bokach AB, BC, CD i DA
umieszczono odpowiedno punkty K, L, M, N takie, że AN=1, CM=2 i BK=2BL. W jakim stosunku
punkt K podzielił bok AB jeśli wiemy, że wyrażenie KL
2+LM
2+MN
2+NK
2 osiąga najmniejszą
możliwą wartość?
4. W czworokąt można wpisać okrąg i jego przekątne są prostopadłe. Wykaż, że iloczyny długości
przeciwległych boków są równe.
5. Odcinek łączący środki ramion trapezu rozcina ten trapez na dwie figury, z których jedna ma
pole 11cm
2, a druga 7cm
2. Oblicz pola figur, na które rozcina ten trapez jego przekątna
11 sty 20:35
Rafal: 1)
https://matematykaszkolna.pl/forum/330868.html gdzieś tu jest podobne
2) oznacz przez X, Y i Z punkty przecięcia prostych AS, BS i CS z bokami BC, AC i AB, dalej
uzasadnij, że punkt S to środek ciężkości trójkąta ABC, następnie zauważ, że CZ=1/2AB (pytanie
pomocnicze: gdzie leży środek okręgu opisanego na tym trójkącie?), na końcu zastosuj kilka
razy twierdzenie Pitagorasa
3) rysunek, twierdzenie Pitagorasa cztery razy, funkcja kwadratowa, ekstremum itd.
4) oznacz przez x, y, z i t długości odcinków, na jakie dzieli przekątne punkt przecięcia,
korzystając z twierdzenia Pitagorasa, napisz równanie wynikające z faktu, że w czworokąt da
się wpisać okrąg, podnieś je do kwadratu, uporządkuj i voila
12 sty 17:07
Rafal: 5) oznacz przez a i b długości podstaw (a>b), wykaż, że linia środkowa ma długość (a+b)/2 i
jest równoległa do podstaw (dowód wygooglujesz), zauważ, że wysokości powstałych trapezów są
tej samej długości (poszukaj trójkątów podobnych), więc stosunek pól tych trapezów zależy
tylko od sumy długości ich podstaw − z odpowiedniej równości uzależnisz od siebie długości
podstaw, potem coś pokombinuj podobnie z tym wyjściowym trapezem.
12 sty 17:20
Pełcio: W 4 zadaniu mi wyszło x=y i t=z, to tak ma być?

12 sty 18:46
12 sty 20:41
Eta:
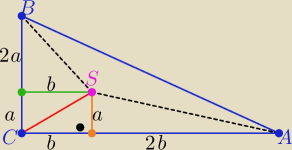
2/
Z treści zadania ...... oznaczenia na rysunku ( 3 pola P
1 równe to P(ABC)= 3P
1
|SA|
2+|SB|
2=5 −− z treści zad.
oraz z tw. Pitagorasa :
|SA|
2=a
2+4b
2
|SB|
2=4a
2+b
2
+ −−−−−−−−−−−−−−−−−−
5=5a
2+5b
2⇒ a
2+b
2=1 ⇒
|CS|=
√a2+b2=
1
12 sty 20:51
Eta:
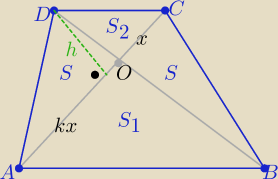
1/
ΔABO ∼ ΔDCO w skali k
| | 1 | |
S1= k2*S2 i S=k*S2 ⇒ S2= |
| *S to S1= k*S |
| | k | |
P trapezu= S
1+S
2+2S ⇒
P =..................
12 sty 20:59
Mila:
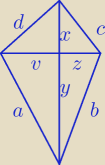
zadanie 4.
a+c=b+d
1) sumy kwadratów przeciwległych boków są równe:
a2+c2=b2+d2
a
2+c
2=v
2+y
2+x
2+z
2
d
2+b
2=x
2+v
2+y
2+z
2
2) przekształcamy
(a+c)
2−2ac=(d+b)
2−2db⇔
ac=db
cnw
12 sty 21:23
Pełcio: Dziękuję pięknie.

12 sty 21:24
Pełcio: Racja Milu, za daleko w to poszedłem. Twoje jest o niebo lepsze

12 sty 21:25
Mila:
Ładne te zadania.

12 sty 21:56
Pełcio: Te są z lokalnego konkursu wojewódzkiego.
Właśnie się dowiedziałem wczoraj, że przeszedłem z OMa do II etapu, pasuje coś poćwiczyć

To tamtym wiadomo nie dorasta, ale od czegoś trzeba zacząć

12 sty 22:00
Eta:
Gratulacje i ........

12 sty 22:02
niematematyk: no widzisz, było cierpliwości, a owoce się znajdą
12 sty 22:07
Mila:
Gratulacje

12 sty 22:08
Pełcio: Dziękuję

Wydaję mi się że bardziej realny na tą chwilę jest AGH. Chociaż tam też ciężko, bo
jestem w IIkl i ciągi, prawdopodobieństwo i jeszcze parę rzeczy to słabo

Ale trochę
spróbuję poćwiczyć

12 sty 22:27
niematematyk: ciągi toż to banał, prawdopodobieństwo, nie wiem co to znaczy xD, gdy ja przerabiałem
probabilistykę, toż to był poziom abstrakcji, zależy jak bardzo rozłożysz zadanie na czynniki,
taki wynik dostaniesz,
12 sty 22:28
niematematyk: nigdy nie jest spójne i jednoznaczne, zawsze znajdzie się ktoś, kto weźmie pod uwagę dodatkowe
warunki, i wynik będzie inny, zależy jak by na to patrzeć, jak to dokładne ma byc
12 sty 22:29
Pełcio: Mi bardziej chodziło o to, że jeszcze tego nie miałem

A Ameryki nie odkryjesz jak nie wiesz
jak się za coś zabrać

12 sty 22:59
 To są pewnie dość proste zadania, ale z geometrii mi idzie zdecydowanie najsłabiej...
1. W trapezie ABCD (AB||CD) przekątne AC i BD przecinają się w punkcie O takim, że
AO : OC=k (k>1). Pole trójkąta AOD=P. Wyznacz w zależności od P i k pole trapezu.
2. W trójkącie prostokątnym o przeciwprostokątnej AB, wybrano punkt S, dla którego trójkąty
SAB, SBC i SAC mają równe pola. Wiedząc, że SA2+SB2=5, oblicz SC.
3. W prostokącie ABCD dane są długości boków AB=5 i AD=2. Na bokach AB, BC, CD i DA
umieszczono odpowiedno punkty K, L, M, N takie, że AN=1, CM=2 i BK=2BL. W jakim stosunku
punkt K podzielił bok AB jeśli wiemy, że wyrażenie KL2+LM2+MN2+NK2 osiąga najmniejszą
możliwą wartość?
4. W czworokąt można wpisać okrąg i jego przekątne są prostopadłe. Wykaż, że iloczyny długości
przeciwległych boków są równe.
5. Odcinek łączący środki ramion trapezu rozcina ten trapez na dwie figury, z których jedna ma
pole 11cm2, a druga 7cm2. Oblicz pola figur, na które rozcina ten trapez jego przekątna
To są pewnie dość proste zadania, ale z geometrii mi idzie zdecydowanie najsłabiej...
1. W trapezie ABCD (AB||CD) przekątne AC i BD przecinają się w punkcie O takim, że
AO : OC=k (k>1). Pole trójkąta AOD=P. Wyznacz w zależności od P i k pole trapezu.
2. W trójkącie prostokątnym o przeciwprostokątnej AB, wybrano punkt S, dla którego trójkąty
SAB, SBC i SAC mają równe pola. Wiedząc, że SA2+SB2=5, oblicz SC.
3. W prostokącie ABCD dane są długości boków AB=5 i AD=2. Na bokach AB, BC, CD i DA
umieszczono odpowiedno punkty K, L, M, N takie, że AN=1, CM=2 i BK=2BL. W jakim stosunku
punkt K podzielił bok AB jeśli wiemy, że wyrażenie KL2+LM2+MN2+NK2 osiąga najmniejszą
możliwą wartość?
4. W czworokąt można wpisać okrąg i jego przekątne są prostopadłe. Wykaż, że iloczyny długości
przeciwległych boków są równe.
5. Odcinek łączący środki ramion trapezu rozcina ten trapez na dwie figury, z których jedna ma
pole 11cm2, a druga 7cm2. Oblicz pola figur, na które rozcina ten trapez jego przekątna

 2/
Z treści zadania ...... oznaczenia na rysunku ( 3 pola P1 równe to P(ABC)= 3P1
|SA|2+|SB|2=5 −− z treści zad.
oraz z tw. Pitagorasa :
|SA|2=a2+4b2
|SB|2=4a2+b2
+ −−−−−−−−−−−−−−−−−−
5=5a2+5b2⇒ a2+b2=1 ⇒ |CS|= √a2+b2= 1
2/
Z treści zadania ...... oznaczenia na rysunku ( 3 pola P1 równe to P(ABC)= 3P1
|SA|2+|SB|2=5 −− z treści zad.
oraz z tw. Pitagorasa :
|SA|2=a2+4b2
|SB|2=4a2+b2
+ −−−−−−−−−−−−−−−−−−
5=5a2+5b2⇒ a2+b2=1 ⇒ |CS|= √a2+b2= 1
 1/
ΔABO ∼ ΔDCO w skali k
1/
ΔABO ∼ ΔDCO w skali k
 zadanie 4.
a+c=b+d
1) sumy kwadratów przeciwległych boków są równe: a2+c2=b2+d2
a2+c2=v2+y2+x2+z2
d2+b2=x2+v2+y2+z2
2) przekształcamy
(a+c)2−2ac=(d+b)2−2db⇔
ac=db
cnw
zadanie 4.
a+c=b+d
1) sumy kwadratów przeciwległych boków są równe: a2+c2=b2+d2
a2+c2=v2+y2+x2+z2
d2+b2=x2+v2+y2+z2
2) przekształcamy
(a+c)2−2ac=(d+b)2−2db⇔
ac=db
cnw



 To tamtym wiadomo nie dorasta, ale od czegoś trzeba zacząć
To tamtym wiadomo nie dorasta, ale od czegoś trzeba zacząć 


 Wydaję mi się że bardziej realny na tą chwilę jest AGH. Chociaż tam też ciężko, bo
jestem w IIkl i ciągi, prawdopodobieństwo i jeszcze parę rzeczy to słabo
Wydaję mi się że bardziej realny na tą chwilę jest AGH. Chociaż tam też ciężko, bo
jestem w IIkl i ciągi, prawdopodobieństwo i jeszcze parę rzeczy to słabo  Ale trochę
spróbuję poćwiczyć
Ale trochę
spróbuję poćwiczyć 
 A Ameryki nie odkryjesz jak nie wiesz
jak się za coś zabrać
A Ameryki nie odkryjesz jak nie wiesz
jak się za coś zabrać 