Matura . grthx: Na jutro dla przyszlych maturzystow Zadnie nr 1 Dla jakiej wartosci parametru a rownanie 3x²−xloga+1=0 ma pierwiastki rzeczywiste spelniajace warunek x₁²+x₂²=1 Zadanie nr 2 Znajdz rownanie stycznych do okregu

	π
x2+y2−8x−10y=28=0 i nachylonych do prostej 5x−y+3=0 pod kątem		.
	4

Zadanie nr 3 W polokrag o promieniu R wpisano trapez ktorego podstawa jest srednica okregu Dla jakiego kąta przy podstawie trapezu pole trapezu jest najwiekszse . Zadanie nr 4 Przekątne AC i BD trapezu ABCD o podstawach AB i DC przecinaja sie w punkcie O Majac dane pola P₁ i P₂ trojkątow ABO i CDO oblicz pole trapezu . Zadanie nr 5 Dziesieciu chlopcow wybralo sie na wycieczke rowerowa jadac gesiego Janek i Franek oraz Bronek znajduja sie w grupie chlopcow Ja Jakie jest prawdopodobienstwo ze : a) Janka Franka i Bronka nikt nie przedziela b) Janek i Franek znajduja sie obok siebie ,a Bronka od Janka i Franka przedziela conajmniej jeden z chlopcow . Znajc zycie pewnie tez podlacza sie tez CI ktorzy juz pisali mature

Krzysiek: Zad 1. a>0 x₁² + x₂² = 1 (x₁+x₂)² − 2x₁x₂ = 1 (^−b_a)² − 2^c_a = 1 ^log2a₉ − ²₃ = 1 ^log2a₉ = ⁵₃ log²a = 15 loga = √15 v loga = −√15 a = 10^√15 v a 10^−√15

grthx: Odpowiedz prawidlowa choc najpierw nalezalo wyznaczyc dziedzine do ktorej nalezy a

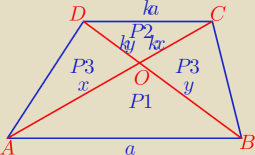
Rafał: Zadanie 4 P₃=[AOD]=[ABD]−[ABO]=[BAC]−[ABO]=[BOC] Wykażemy, że w dowolnym trapezie P₃=√P₁*P₂. W tym celu przyjmijmy, że trójkąt CDO jest podobny do trójkąta ABO w kali k. Wówczas P₂=P₁*k², a zatem wystarczy pokazać, że

	P3
P3=√P1*k2*P1=P1*k, czyli		=k. Widzimy, że trójkąty ABO i BOC mają wspólną
	P1

wysokość opuszczoną z wierzchołka B na prostą AC. Wobec tego stosunek ich pól zależy tylko i wyłącznie od stosunku długości boków CO i AO, który wynosi k. To kończy dowód, że pole P całego trapezu wynosi P=P₁+P₂+2√P₁*P₂=(√P₁+√P₂)².

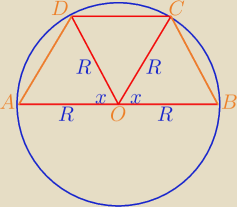
Rafał: Jeśli trapez jest wpisany w okrąg, to jego ramiona muszą mieć tę samą długość. Stąd wynika przystawanie trójkątów AOD i BOC (cecha bok−bok−bok). Pole całego trapezu można przedstawić jako sumę pól trójkątów AOD, BOC i COD.

	1
[AOD]=		*R*R*sinx
	2

	1
[BOC]=		*R*R*sinx
	2

	1		1
[COD]=		*R*R*sin(180−2x)=		*R*R*sin2x
	2		2

	1		1
[AOD]+[BOC]+[COD]=		R2(2sinx+sin2x)=		R2(2sinx+2sinxcosx)=R2(sinx+sinxcoxs)
	2		2

f(x)=sinx+sinxcosx f'(x)=cosx+(cosx*cosx+sinx*(−sinx))=cosx+cos²x−sin²x=2cos²+cosx−1=0

	1
cosx=−1 lub cosx=
	2

	1
W pierwszym przypadku mamy sprzeczność, bo x ma być kątem ostrym. Wobec tego cosx=		,
	2

czyli x=60. Ostatecznie, spośród wszystkich rozpatrywanych trapezów największe pole ma ten, którego kąty wewnętrzne wynoszą kolejno: 60, 60, 120, 120.

ICSP: dorzuce jedno od siebie: Rozwiązać równanie: 5³√9 − x² − 4³√(3 − x)² = ³√(3 + x)² D : x ∊ R

yht: To ja też Zad. 7 Trzecim wyrazem ciągu arytmetycznego (a_n) jest a₃=3, zaś piąty wyraz jest odwrotnością ósmego wyrazu. Wyznacz a₁ jeśli wiadomo, że a₆>0.

Benny: 3−x=a 3+x=b 5(ab)^1/3=4a^2/3+b^2/3 /()³ 125ab=64a²+48a^4/3b^2/3+12a^2/3b^4/3+b² 125ab=64a²+12(ab)^2/35ab^1/3+b² 125ab=64a²+60ab+b² 64a²−65ab+b²=0 (8a−b)²−49ab=0 (21−9x)²−49(9−x²)=0 441−378x+81x²−441+49x²=0 130x²−378x=0

yht: 5 ³√9−x² − 4 ³√(3−x)² = ³√(3+x)² 5 ³√(3−x)(3+x) − 4 ³√(3−x)(3−x) = ³√(3+x)(3+x) 4 ³√(3−x)(3+x) + ³√(3−x)(3+x) − 4 ³√(3−x)(3−x) = ³√(3+x)(3+x) 4 ³√(3−x)(3+x) − 4 ³√(3−x)(3−x) = ³√(3+x)(3+x) − ³√(3−x)(3+x) 4³√3−x(³√3+x − ³√3−x) = ³√3+x(³√3+x−³√3−x) 4³√3−x(³√3+x − ³√3−x) − ³√3+x(³√3+x−³√3−x) = 0 (4³√3−x − ³√3+x)*(³√3+x−³√3−x) = 0 4³√3−x − ³√3+x = 0 lub ³√3+x−³√3−x = 0 4³√3−x = ³√3+x |()³ lub ³√3+x = ³√3−x |()³ 64(3−x) = 3+x lub 3+x = 3−x 192−64x = 3+x lub x+x = 3−3 −64x−x = 3−192 lub 2x = 0 |:2 −65x = −189 |:(−65) lub x=0

	189
x =		lub x=0
	65

Rafał: a₁+2r=3

	1
a1+4r=
	a1+7r

a₁=3−2r

	1
3+2r=
	3+5r

(3+2r)(3+5r)=1 9+15r+6r+10r²=1 10r²+21r+8=0 Δ=121

	−21−11
r=		=−1,6 oraz a1=6,2 (sprzeczność, bo a6=6,2−5*1,6=−1,8<0)
	20

lub

	−21+11
r=		=−0,5 oraz a1=4
	20

a₅=2 a₈=0,5

grthx: To sa zadania ze starej matury wiec nie ma podzialu na podstawe i rozszsrzenie dzisiaj dostalem ksiazki od Qulki (zaraz muszse jej podziekowac i mam testy maturalne poziom podstawowy ale 2002−2004 r Moge jeden z testow specjalnie dla Ciebie napisac jesli chcesz .

grthx: Wobec tego popoludniu specjalnie dla ciebie napisze w nowym poscie Teraz czuje sie troche zle i tylko obserwuje . Ale bede pamietal .

grthx: Skoro zdales na 50% to w takim razie skup sie teraz na pomocy dla innych maturzystow(bo cos umiesz ) i nie wracajmy juz do tego tematu