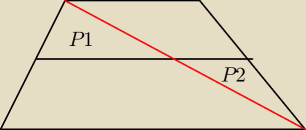
 Odcinek łączący środki ramion trapezu rozcina ten trapez na dwie figury, z których jedna ma
pole 11cm2 a druga 7cm2 Oblicz pola figur, na które rozcina ten trapez jego przekątna
Tyle co udało mi się zrobić (nie wiem czy dobrze bo koniec końców krążę w kółko):
7/18 = P1/11−P2+P1
P1=7−7/11P2
Oczywiście to P1 i P2 to tak pomocniczo, w zadaniu chodzi o pola całych trójkątów, które tworzy
przekątna.
Odcinek łączący środki ramion trapezu rozcina ten trapez na dwie figury, z których jedna ma
pole 11cm2 a druga 7cm2 Oblicz pola figur, na które rozcina ten trapez jego przekątna
Tyle co udało mi się zrobić (nie wiem czy dobrze bo koniec końców krążę w kółko):
7/18 = P1/11−P2+P1
P1=7−7/11P2
Oczywiście to P1 i P2 to tak pomocniczo, w zadaniu chodzi o pola całych trójkątów, które tworzy
przekątna.
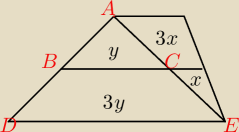 x+3y = 11
3x+y = 7
x+3y = 11
3x+y = 7
| 1 | ||
Wysokosc trojkata ABC jest dwa razy mniejsza niz ADE, to samo podstawa |BC| = | |DE|, wiec | |
| 2 |
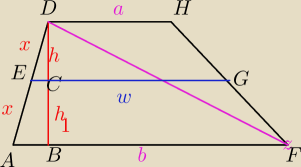 z trojkatow podobnych :
z trojkatow podobnych :
| h | h+h1 | ||
= | |||
| x | 2x |
| a+b | ||
w = | ||
| 2 |
| 1 | ||
P = | * (w + b) * h = 11 | |
| 2 |
| 22 | ||
(w + b) * h = 22 −−−>> h = | ||
| w+b |
| 1 | ||
P = | * (a+w) * h = 7 | |
| 2 |
| 14 | ||
(a+w) * h = 14 −−−>>> h = | ||
| a+w |
| 22 | 14 | ||
= | |||
| w+b | a+w |
| a+b | ||
22a − 14b + 8( | ) | |
| 2 |
| 13 | ||
b = | a | |
| 5 |
| 1 | 1 | 13 | ||||
P = | * h * b = | * h * | a | |||
| 2 | 2 | 5 |
| 1 | 1 | 1 | 1 | |||||
P2 = | (a+b)*h − | * h * b = | h(a+b−b) = | h * a | ||||
| 2 | 2 | 2 | 2 |
| P |
| 13 | |||||||||||||||
= | = | ||||||||||||||||
| P2 |
| 5 |
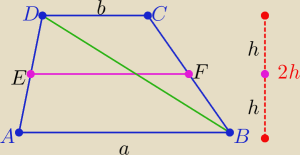
| 1 | ||
Szukane pole ΔBCD = | b*2h= b*h i pole ΔABD= a*h | |
| 2 |
| a+b | ||
|EF|= | oznaczam jako |d | |
| 2 |


