Problem Maja: Oblicz sumę rozwiązań równania x²−2x+1=0. Ile być powinno? Wg mnie 1 a moja nauczycielka mówi że 2.

5-latek:

	b
x1+x2= −
	a

Maja: Ale rozwiązanie jest tylko 1 to jak można liczyć jego sumę ?

5-latek: x²−2x+1= (x−1)² zatem Δ=0 wiec rozwiazania istnieja . Mozesz stosowac wzory Viete'a

Adamm: 5−latek, rozwiązanie równania jest tylko jedno, jest to 1 zatem suma rozwiązań wynosi 1

Maja: No jak patrzę to w zadaniach w takich przypadkach niektórzy liczą sumę jako 2. Jak mam na maturze napisać ?:(

Adamm: tak jak jest logicznie, czyli 1

5-latek: Tak rozwiazanie jest x=1 dla Δ=0 sa dwie konwencje okreslenia liczby pierwiastkow rownania kawdratowego czasem mowi sie ze rownanie takie ma jeden pierwiastek (podwojny) Czasem ze dwa rowne pierwiastki

Adamm: uzasadnisz to jakoś ładnie, i będzie w porządku nie słuchaj innych tylko swojego rozsądku, rozwiązanie przecież jest tylko jedno

Adamm: przecież wiem, ale mówimy właśnie o rozwiązaniach

Maja: Niby matematyka przedmiot ścisły a takie niedomówienia A potem z klasówki dostaje zła ocenę

Adamm: niedomówienia? wszystko jest jasne jak słońce trzeba było się sprzeczać z nauczycielką

5-latek: Nie jestem az tak w tym dobry ale sugeruje sie tym co np piszsa P Zakrzewscy w swijej ksiazce Moze ktos sie tes wypowie

Adamm: mówimy o rozwiązaniach, rozwiązanie jest jedno, to nie jest to samo co pierwiastek wielomianu

Maja: Co piszą ci Zakrzewscy?

mataw69: (x−x₁)(x−x₂) = x²−(x₁+x₂)x+x₁x₂ Czylo w twoim przypadku x₁+x₂ = 2

pawjan: 1 jest PODWÓJNYM miejscem zerowym z tego wynika ( i ze wzorów viete) ze suma jest 2

Adamm: pawjan, "miejscem zerowym", nie rozwiązaniem radzę nauczyć się terminologii zanim zacznie się kogoś pouczać

pawjan: miejsce zerowe funkcji po lewej stronie jest rozwiazaniem równania

Adamm: to jest właśnie liceum, i okradanie ludzi z własnych mózgów, bo wpaja się im myślenie schematyczne

pawjan: radze paczeć

pawjan: lepiej iść za głosem serca i mieć źle na maturze co może czasem przesądzić że nie dostaniemy sie na wymarzone studia

Adamm: "iść za głosem serca" <− właśnie to robisz, bez myślenia, pozbawiona własnego zdania wypowiedź, i mówię tu oczywiście o matematyce żaden szanujący się matematyk nie zaliczył by ci gdybyś napisał że suma rozwiązań wynosi 2

Bogdan: Można spotkać stwierdzenie, że przy Δ = 0 są dwa równe rozwiązania, albo że jest jedno rozwiązanie podwójne, natomiast przy Δ > 0 są dwa różne rozwiązania. Tak widząc przedstawiony tu problem otrzymujemy: x² − 2x + 1 = 0 ⇒ (x − 1)*(x − 1) = 0 x₁ = 1, x₂ = 1, x₁ + x₂ = 2

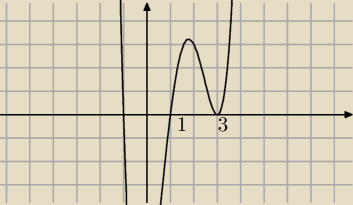
maja: pawjan to oblicz sumę miejsc zerowych tej funkcji

pawjan: nie zaliczyłby odpowiedzi skoro tak jest w kluczu?

Adamm: Bogdan, tu masz błąd "rozwiązania" nigdy się tak nie mówi funkcja a równanie to co innego jeśli ktoś tak powie to popełnia błąd logiczny

Adamm: pawjan, powiedziałem szanujący się matematyk, nie taki co sprawdza bez namysłu

maja: Bogdan a kiedy mam wiedzieć którą "opcję" stosować?

5-latek: Witaj Bogdan

pawjan: odnośnie miejc zerowych miałem na mysli przedstawione równanie, poniewaz liczenie x² −2x +1= 0 to tak jak wyznaczanie miejsc zerowych funkcji (x−1)²

Adamm: pawjan, wyznaczanie miejsc zerowych, owszem, jest tylko jedno takie miejsce, 1 najpierw pomyśl zanim coś napiszesz

pawjan: https://matematykaszkolna.pl/strona/2020.html

yht: nie będzie trzeba rozstrzygać takich rzeczy na maturze na maturze piszą wyraźnie "dwa różne rozwiązania"

pawjan: jest 1 rozwiązanie ale nie jest to takie samo 1 rozwiązanie jak w przypadku x−1=0

maja: pawjan bardzo proszę o podanie sumy miejsc zerowych funkcji narysowanej powyżej bo się z toba nie zgadzam w tej kwestii

Adamm: pawjan, szczęścia w życiu życzę, daleko na tej logice nie pojedziesz

maja: yht, ale na klasówkach w szkole już tak

Adamm: na stronie jest błąd, powinno być napisane "pierwiastek krotny", zostało tak napisane żeby ktoś obcy z pojęciami to zrozumiał

pawjan: odnośnie miejc zerowych miałem na mysli przedstawione równanie, poniewaz liczenie x² −2x +1= 0 to tak jak wyznaczanie miejsc zerowych funkcji (x−1)² nie wiemy dlajakiego argumentu wykres przecina os OX dla x<0

maja: dla x=−1

pawjan: mysle ze logike mam nie najgorszą a do szczesliwego zycia nie potrzebna mi pełna wiedza na temat tego zagadnienia

Adamm: wiemy, dla żadnego

yht: byłbym za jednym rozwiązaniem x=1, więc suma rozwiązań równa 1 ale można się kłócić to taki podobny problem do tego czy 0 jest liczbą naturalną

pawjan: to 3

Adamm: (x−1)²=0 \*(x−1) (x−1)³=0 ze wzorów vieta x₁+x₂+x₃=3, więc suma rozwiązań równa się 3 (nie piszę tego bo tak uważam, ma to pokazać myślenie innych)

pawjan: (x−1)³ to zupełnie inna funkcja niz (x−1)²

pawjan: (bez zupełnie)

Adamm: ale przejście jest równoważne, logika, coś co powinieneś znać podobno twoja logika jest bez zarzutów, heh koniec dyskusji, nie rozmawiam z tobą więcej

Bogdan: Napisałem Adammie "można spotkać stwierdzenie, że przy Δ = 0 są dwa równe rozwiązania", użyłem słowa "rozwiązania" bo w zadaniu maji podane jest równanie. http://www.matmana6.pl/tablice_matematyczne/liceum/funkcja_kwadratowa/84-wzory_vietea a także w innych źródłach używa się określenia "rozwiązania"

pawjan: gdybys miał za zadanie obliczyc sume rozwiazan rownania x³ −3x² +3x−1=0 to suma = 3 jak policzyłes

maja: Czyli sam mylisz się w tym co twierdzisz Ta suma wg tego co podajesz może być też równa 10 i 30 i 50 i 60 itd. Wielomian mógł mieć wzór w(x)=(x−1)(x+1)(x−3) , ale również w(x)=(x−1)³(x+1)⁷(x−3)²

pawjan: Adamie radziłbym nie uzywac nadmiernie ironii wzgledem innych koniec dyskusji, nie rozmawiam z tobą więcej

Adamm: no dobra, to co napisałeś Bogdanie, było raczej kwestią sporną, nie powinienem był się o to czepiać, schodzę z drogi co do kwestii pawjana, moje zdanie pozostaje

pawjan: Adamie radziłbym nie uzywac nadmiernie ironii wzgledem innych koniec dyskusji, nie rozmawiam z tobą więcej

Adamm: maja, właśnie, pewnie to i tak jest tylko troll, próbuje wprowadzać w błąd innych, albo po prostu ten z "mądrzejszych", też się tacy zdarzają

pawjan: ja tylko mowie jak mnie uczyła moja pani od matematyki nikomu nie narzucam mojego toku myslenia a juz na pewno nie jestem trollem

pawjan: wydaje mi sie ze za tego madrzejszego uwaza sie niejaki pan adam

Omikron: Moim zdaniem wszystko tutaj jest jasne. By rozwiązać równanie doprowadzamy je do postaci x=... Cokolwiek by nie było, czy (x−1)²=0, czy (x−1)³=0, czy (x−1)¹⁰⁰=0, to ostatecznie dochodzimy do postaci x=1 Jest więc jedno rozwiązanie, suma rozwiązań wynosi 1 i tyle.

5-latek: To czyli Twoim zdaniem liczba rozwiazan rownania to inaczej suma rozwiazan? Rozwiazanie rownania (dla jedenej zmiennej jest okreslane tez jako pierwiastek rownanania Specjalny wyklad algebry elemnetarnej Nowosiolow . Niech rownanie kwadratowe ma dwa rozwiazania x=5 i x=−3 Ile wymosi suma rozwiaazn tego rownania ?

5-latek: Inaczej x=10 i x=−5

Omikron: Nie nie, tylko w tym przypadku suma to 1, jakby x równało się 7 to sumą byłoby 7

mataw69: Suma rozwiązań jest równa 2, suma różnych rozwiązań jest równa 1.

5-latek: WItaj ja jestem tego zdania co Bogdan . Ciekawe co powiedzieliby na ten temat w CKE

Adamm: tak jak powiedział yht, teraz nie ma takich problemów, bo pisze się takie rzeczy wyraźnie

maja: wg mnie x−1=0 − rozwiązanie to liczba 1 − suma 1 (x−1)²=0 − rozwiązanie to liczba 1 − suma 1 (x−1)¹⁰⁰=0 − rozwiązanie to liczba 1 − suma 1 (x−1)(x−2)=0 rozwiązania to liczby 1 i 2 − suma 3

Adamm: skończmy temat, zadanie było banalne, i tak naprawdę to nie ma tu nic do gadania suma to 1 i tyle, nie ma pośrednich czy prawie−poprawnych innych odpowiedzi zadanie jest postawione bardzo jasno, nie spamować

misiek: moim zdaniem odp to 2 nie chodzi o ilosć rozwiązań tylko o ich sumę rozwiązaniem równania jest liczba 2 więc suma naturalnie równa się 2

Krzysiek: Suma to 2

Maja: Rozwiązaniem jest liczba 2 , którego ?

Maja: Krzysiek dlaczego ? Popatrz na wykres z 21.12 i powiedz : ile jest równa suma pierwiastków tego wielomianu ?

Krzysiek: 2k*3+(2n+1)*1 Skąd wiesz że wszystkimi rozwiązaniami równania (x−1)¹⁰⁰=0 jest x=1? No okej, widzimy że dla x=1 lewa strona się zeruje, (x−1)(x−1)⁹⁹=0 Dodajemy 1 do sumy rozwiązań Suma rozwiązań: 1 Teraz musimy znaleźć sumę rozwiązań równania (x−1)⁹⁹=0 x=1, dodajemy znów 1 do sumy rozwiązań Suma rozwiązań: 2 Trzeba znaleźć sumę rozwiązań równania (x−1)⁹⁸ I tak dalej... Dochodzimy do tego że suma rozwiązań to 100 Moje rozwiązania to: x₁=1, x₂=1, ... , x₁₀₀=1 Nie obchodzi nas to, że te rozwiązania są takie same

Omikron: Jak to nas nie obchodzi? To jest jedno i to samo rozwiązanie, nie rozumiem, dlaczego liczysz je 100 razy.

Bogdan: dla Krzyśka

Eta: I ode mnie też.............. dla Krzyśka

Ajtek: Krzysiek

Słaby gracz: Nie wiem czy problem został rozwiązany, ale rozwiązaniem równania x²−2x+1=0 jest x=1. Ponieważ jest to równanie kwadratowe zatem oczywiste jest, że rozwiązania równania są dokładnie dwa, dokładniej mówiąc dwa identyczne rozwiązania. Jakby zapisać to równanie w postaci iloczynowej to będzie wyglądało ono w następujący sposób (x−1)(x−1)=0. Po wymnożeniu otrzymamy trójmian który jest u góry. Zatem suma rozwiązań po wyliczeniu x1 i x2 powinna być równa 2, gdyż x1 = −b+√Δ/2a = 1 oraz x2 = −b−√Δ/2a = 1. Ze wzorów Vieta powinno wyjść dokładnie to samo. x1+x2 = −b/a = −(−2)/1 = 2/1 = 2. Jeszcze jedno. Nie ma możliwości by przy równaniu kwadratowym wyszło jedno rozwiązanie. Zawsze wychodzą 2 rozwiązania, mogą wyjść 2 takie same, ale zawsze są 2. Uwzględnianie dziedziny swoją drogą

Eta: @ Słabego gracza czytałeś ?.........wpis Bogdana 21:11

lwg: (x−1)ⁿ = 0, gdzie x jest elementem {...,−3,−2,−1,0,1,2,3,...}, a n jest liczbą całkowitą dodatnią. Zbiór rozwiązań {1} jest jednoelementowy. Rozwiązanie jest więc dokładnie jedno, ale czy jest ono pojedyncze, podwójne, potrójne, ..., n−te − podkreślamy tylko po to, aby mieć obraz równania wyjściowego, będącego dwumianem (dwumianem stopnia pierwszego), trójmianem (dwumianem stopnia drugiego), bikwadratem (dwumianem stopnia czwartego), ..., dwumianem stopnia n−tego.

lwg: Zbiór rozwiązań {1} jest jednoelementowy. Rozwiązanie jest więc dokładnie jedno, ale czy jest ono pojedyncze, podwójne, potrójne, ..., n−te − podkreślamy tylko po to, aby mieć obraz równania wyjściowego, będącego dwumianem (dwumianem stopnia pierwszego), trójmianem (dwumianem stopnia drugiego), czwórmianem (dwumianem stopnia trzeciego), pięciomianem (dwumianem stopnia czwartego), sześciomianem (dwumianem stopnia piątego), ... , (n+1)mianem (dwumianem stopnia n−tego).

pawjan: mam nadzieje ze adamm sobie to przeczyta

maja: od kiedy to zbiór rozwiązań równania (x−1)¹⁰⁰=0 ma 100 elementów?

maja: Krzysiek czekam aż napiszesz ile jest równa suma pierwiastków wielomianu narysowanego o 21.12

Omikron: pawjan, akurat Iwg podziela zdanie Adama (i moje też) https://matematykaszkolna.pl/forum/338827.html

5-latek: A dlaczego czekasz ? Daczego sobie nie napiszsesz do CKE o wyjasnienie problemu ? . ja wlasnie napisalen emalia przed chwilad o do nich w tej sprawie . Mozesz przeciez zrobic tak samo .

zef: Która wersja jest w końcu poprawna ?

pawjan: mówiłem o krzysku

Adamm: żeby odpowiedzieć na to pytanie wystarcza podać definicję rozwiązania równania dla mnie rozwiązanie równania f(x)=0, gdzie f jest funkcją, jest zbiór wszystkich x∊ℛ takich że f(x)=0 zachodzi i zgodnie z tą definicją zbiór wszystkich rozwiązań równania (x−1)²=0 to {1}, zatem suma wszystkich rozwiązań wynosi 1

Omikron: Równoważną postacią równania (x−1)²=0 jest x−1=0 (stosujemy poprawne peirwiastkowanie stronami). Idąc waszą logiką suma rozwiązań pierwszego równania to 2, drugiego 1. Ponieważ te postacie równania są sobie równoważne to 2=1

Adamm: pawjan, ile to jest pół tora razy 2

zef: nie możesz powiedzieć że (x−1)²=x−1 te 2 równania nie są równoważne.

Adamm: 2=2 ⇔ 1=1 ale nie wynika z tego że 2=1

Omikron: Nie są równe, są równoważne. (x−1)²=0⇔x−1=0

Adamm: nieważne, to jest inny przypadek zresztą, można powiedzieć że (x−1)²=x−1, kto ci zabrania?

zef: (x−1)²=0 Można to zapisać tak: (x−1)(x−1)=0 Pytają o sumę "rozwiązań", a rozwiązanie jest tylko jedno i jest to liczba 1 Więc odp to 1.

Adamm: ( (x−1)²=0 ⇔ x−1=0 ) ⇒ (x−1)²=x−1

Omikron: Jeżeli jedno równanie można doprowadzić do drugiego, to jak suma rozwiązań każdego z nich może być różna?

Ziomek: 1+0,(9)=2 wiecie o tym

Eta: 2017,(9)= 2018

Omikron: No prawda, tak też można powiedzieć, ale nie chodziło mi o to

Omikron: To do Adama

Adamm: raczej (x−1)²=0 ⇔ x−1=0 ⇒ (x−1)²=x−1

5-latek: Za chwile w tym temacie dojdziemy do absurdu .

Omikron: Dla mnie absurdem jest to że suma rozwiązań równania o jednym rozwiązaniu równym 1 wynosi 2.

zef: Skoro jest jedno rozwiązanie to chyba logiczne że suma rozwiązań równania jest równa temu x_o.

Adamm: a 0,(9)≠1 bo 0,(9)+ε=1 5−latek, my żyjemy absurdem, to matematyka

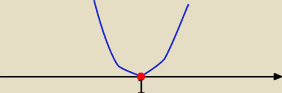
Eta: x= 1 pierwiastek dwukrotny ( bo mamy odbicie wykresu)

Adamm: matematyka jest w porządku, dopóki trzymamy się ustalonych aksjomatów i definicji takie mówienie sobie, o (x−1)²=0 ma dwa rozwiązania bo jest 1 i 1 to jest wymyślanie sobie własnych definicji

Eta: 0,(9)=x 9,(9)=10x 9= 9x x=1 to 0,(9)=1

maja: Eta a dlaczego nie 10−krotny?

Adamm: a czy można utworzyć taką nieskończoną uporządkowaną listę że na tej liście znajdą się wszystkie liczby z zakresu od 0 do 1 czemu?

Eta: Może być i 10 krotny (x−1)¹⁰=0

Adamm: nie można

5-latek: To moze inaczej mamy rownanie kwadratowe Δ>0 wiec mamy dwa rozwiazania Ile wynosi suma rozwiazn takiego rownnania .? Dwa ?

	b
czy x1+x2= −		?
	a

Adamm: 5−latek, co innego suma rozwiązań a ich liczba

lwg: Gdzie jest napisane, że zbiór rozwiązań równania (x−1)¹⁰⁰=0 ma sto elementów? Urojenia są dzisiaj w modzie, jednakże Ty Maju nie udajesz. Generalnie, w związku z Twoim przykładem równania x²−2x+1= 0, gdzie x jest elementem {...,−3,−2,−1,0,1,2,3,...}, a n jest liczbą całkowitą dodatnią, chodzi właśnie o równanie (x−1)ⁿ, gdyż x²−2x+1=(x−1)²=(x−1)ⁿ=0. Zbiór rozwiązań jest jednoelementowy równy {1}. Twoja nauczycielka mija się z prawdą. x jest elementem zbioru {1}. Rozwiązanie jest więc dokładnie jedno, ale czy jest ono pojedyncze, podwójne, potrójne, ..., n−te − podkreślamy tylko po to, aby mieć obraz równania wyjściowego, będącego dwumianem (dwumianem stopnia pierwszego), trójmianem (dwumianem stopnia drugiego), czwórmianem (dwumianem stopnia trzeciego), pięciomianem (dwumianem stopnia czwartego), sześciomianem (dwumianem stopnia piątego), ... , (n+1)mianem (dwumianem stopnia n−tego). Suma pierwiastków wynosi 1. Krotność pierwiasta x nie ma wpływu na liczbę rozwiązań równania (x−1)ⁿ.

lwg: Adamm, Nie bredź. Suma rozwiązań jest równa 1. Liczba rozwiązań wynosi 1. Krotność pierwiastaka nie ma wpływu na liczbę rozwiązań. Podwójne, nie znaczy dwa. Sprawdź, czy Cię w domu nie ma.

lwg: Adamm napisał: co innego suma rozwiązań, a ich liczba. Re. Suma rozwiązań jest równa 1. Liczba rozwiązań wynosi 1. Krotność pierwiastaka nie ma wpływu na liczbę rozwiązań. Rozwiązanie podwójne nie oznacza istnienia dwóch rozwiązań. Maja, Gdzie jest napisane, że zbiór rozwiązań równania (x−1)¹⁰⁰=0 ma sto elementów? Generalnie, w związku z Twoim przykładem równania x²−2x+1= 0, gdzie x jest elementem zbioru {...,−3,−2,−1,0,1,2,3,...}, chodzi właśnie o równanie (x−1)ⁿ, gdyż x²−2x+1=(x−1)²=(x−1)ⁿ=0, (1) gdzie n jest liczbą całkowitą dodatnią, Zbiór rozwiązań (1) jest jednoelementowy równy {1}, a jego moc jest równa liczbie 1. Twoja nauczycielka mija się z prawdą. x jest elementem zbioru {1}. Wartość argumentu x należy do zbioru jednoelementowego {1}. Rozwiązanie jest więc dokładnie jedno, ale czy jest ono pojedyncze, podwójne, potrójne, ..., n−te − podkreślamy tylko po to, aby mieć obraz równania wyjściowego, będącego dwumianem (dwumianem stopnia pierwszego), trójmianem (dwumianem stopnia drugiego), czwórmianem (dwumianem stopnia trzeciego), pięciomianem (dwumianem stopnia czwartego), sześciomianem (dwumianem stopnia piątego), ... , (n+1)mianem (dwumianem stopnia n−tego). Suma pierwiastków wynosi 1. Krotność pierwiasta x nie ma wpływu na liczbę rozwiązań równania (x−1)ⁿ.

lwg: Generalnie, w związku z równaniem x²−2x+1= 0, gdzie x jest elementem zbioru {...,−3,−2,−1,0,1,2,3,...}, chodzi właściwie o równanie (x−1)ⁿ, gdyż x²−2x+1=(x−1)²=(x−1)ⁿ=0, (1) gdzie n jest liczbą całkowitą dodatnią, Zbiór rozwiązań (1) jest jednoelementowy równy {1}, a jego moc jest równa liczbie 1. x jest elementem zbioru {1}. Wartość niewiadomej x należy do zbioru jednoelementowego {1}. Istnieje dokładnie jedno rozwiązanie równania (1), ale czy jest ono pojedyncze, podwójne, potrójne,..., n−te − podkreślamy tylko po to, aby mieć obraz równania wyjściowego, będącego dwumianem (dwumianem stopnia pierwszego), trójmianem (dwumianem stopnia drugiego), czwórmianem (dwumianem stopnia trzeciego), pięciomianem (dwumianem stopnia czwartego), sześciomianem (dwumianem stopnia piątego), ... , (n+1)mianem (dwumianem stopnia n−tego). Suma rozwiązań jest równa 1. Liczba rozwiązań wynosi 1. Krotność pierwiastaka x nie ma wpływu na liczbę rozwiązań równania (x−1)ⁿ. Rozwiązanie podwójne czy n−krotne nie oznacza istnienia dwóch czy n rozwiązań. Tak , czy inaczej odpowiadecie za mnie. Tak, właśnie także WY. Nie macie sumień.

beginner: lwg , skoro umiesz coś tam z matmy, to idź na uniwersytet. Tam Ci wyperswadują to od razu.

beginner: No chyba, że jesteś emerytowanym nauczycielem matematyki, który błądzi gdzieś tam i cały czas patrzy w niebo. I pewnie mówi , że wszystko jest trywialne jak skowronsky.

beginner: Co nie znaczy, że błądzi w brodziku intelektualnym.

Bogdan: Ale się rozwinął ten wątek. Myślę, że chyba trzeba się cieszyć, że jakiś mało ważny problem dla przeciętnego przechodnia wywołuje aż tyle emocji, nawet sławny na tym forum lwg wtrącił swoje zdanie (przy okazji − pozdrawiam Cię lwg). Nasuwa się pytanie: czy pierwiastek równania i rozwiązanie (w kontekście np. równanie ma siedem rozwiązań) równania to jest to samo? Wchodzimy w rozważania prawie filozoficzne

Maja: Okazuje się, że kogo nie zapytać to każdy mówi inaczej Zostanę przy takiej opcji: suma rozwiązań 1. CKE wyraźnie pisze w tablicach. Równanie ma jedno rozwiązanie dla Δ=0. Ale jeśli będzie mowa o pierwiastkach to napisze ze uwzględniając krotnosci suma jest 2 a nie uwzględniając 1. Szkoda że co drugi autor podręcznika podaje odmienne wersję.:( dziękuję wszystkim za pomoc

LWG: beginner, Dlaczego łżesz? Co wyperswadują matematycy? Jeszcze raz. Generalnie, w związku z równaniem x²−2x+1= 0, gdzie x jest elementem zbioru {...,−3,−2,−1,0,1,2,3,...}, chodzi właściwie o równanie (x−1)ⁿ, gdyż x²−2x+1=(x−1)²=(x−1)ⁿ=0, (1) gdzie n jest liczbą całkowitą dodatnią, Zbiór rozwiązań (1) jest jednoelementowy równy {1}, a jego moc jest równa liczbie 1. x jest elementem zbioru {1}. Wartość niewiadomej x należy do zbioru jednoelementowego {1}. Istnieje dokładnie jedno rozwiązanie równania (1), ale czy jest ono pojedyncze, podwójne, potrójne,..., n−te − podkreślamy tylko po to, aby mieć obraz równania wyjściowego, będącego dwumianem (dwumianem stopnia pierwszego), trójmianem (dwumianem stopnia drugiego), czwórmianem (dwumianem stopnia trzeciego), pięciomianem (dwumianem stopnia czwartego), sześciomianem (dwumianem stopnia piątego), ... , (n+1)mianem (dwumianem stopnia n−tego). Suma rozwiązań jest równa 1. Liczba rozwiązań wynosi 1, a suma rozwiązań też jest równa 1, bo jest mocą sumy zbiorów rozwiązań (1). Krotność pierwiastaka x nie ma wpływu na liczbę rozwiązań równania (x−1)ⁿ. Rozwiązanie podwójne czy n−krotne nie oznacza istnienia dwóch czy n rozwiązań.

LWG: Maja, Krotność jedynego rozwiązania równania (x−1)²=0, to wykładnik n=2. Masz dwuwymiarowy układ współrzędnych kartezjańskich. Powiesz. Przecież chodzi o równanie, a nie o funkcję. A jak nazwiesz zbiór rozwiązań równania? Jeżeli ten zbiór nie jest określony (nie jest podany), to przyjmujesz, że niewiadoma x jest elementem zbioru liczb rzeczywistych R. x=1, więc x należy do R. Zbiór rozwiązań to {1}. {1} u {1} = {1}. x₁=x₂=x₀=1. Suma rozwiązań wynosi 1, bo zbiory rozwiązań są sobie równe.

LWG: Bogdan, W tym kontekście to jest to samo. Obie Królowe są ważne Filozofia i Matematyka. Rozwiązać równanie, to znaczy odpowiedzieć na pytanie, dla jakich wartości jest ono spełnione. Rozwiązać równanie, to podać wszystkie jego rozwiązania. x − pierwiastek, jedno rozw.; (x,y) − para, jedno rozw.; (x,y,z) trójka, jedno rozwiązanie. (x−1)²=0 ma jedno rozwiązanie. Suma rozwiązań wynosi 1, bo zbiory rozwiązań są sobie równe. Od 03 maja 2016 roku nie dotykam żadnych zadań. To jest koniec. Dziękuję Ci. Pozdrawiam Disproof the Birch and Swinnerton−Dyer Conjecture http://pubs.sciepub.com/EDUCATION/4/7/1/index.html