Wartośc bezwzględna
Cotigopro: |x+1|=|x−1|
Jak to rozwiązać?
Proszę o pomoc!
8 paź 20:09
Nin9:
8 paź 20:13
Cotigopro: Chyba coś Ci się popsuło kolego.
8 paź 20:14
jc: To zbiór punktów, których odległość od −1 jest taka sama, jak odległość od 1, czyli środek,
a konkretnie liczba zero.
8 paź 20:14
Cotigopro: Mógłbyś napisać rozwiązanie?
8 paź 20:16
Cotigopro: Mam na myśli formalne rozwiązanie. Jak rozpisać to krok po kroku.
8 paź 20:16
===:
|a|=|b| a=b lub a=−b
8 paź 20:19
Cotigopro: Czyli dla x >= 0:
|x+1|=|x−1|
x+1 = x−1
x−x =−1−1
0 != −2
dla x < 0
−x−1 = −x + 1
to wychodzi to samo...
8 paź 20:21
Mila:
|x+1|=|x−1| /2 obie strony są nieujemne
x2+2x+1=x2−2x+1
4x=0
x=0
8 paź 20:24
5-latek: No wychodzi to samo
Wobec tego jaki wniosek ?
8 paź 20:24
Cotigopro: @Mila
Czemu obie storony podnioslaś do 2?
8 paź 20:25
5-latek: No przeciez jeslli wychodzi to samo dla x≥0 i x<0 to kazda liczba zbioru liczb ℛ spelnia to
rownanike
Wobec tego po co sie dopytujes ?
8 paź 20:27
Cotigopro: A czy to robie dobrze:
|1−2x|+|2x−6|=x
dla x>=0
1−2x+2x−6
x=−5
dla x < 0
x = 5
?
8 paź 20:28
Mila:
Po pierwsze mogłam, bo obie strony nieujemne.
Po drugie aby rozwiązać równanie.
8 paź 20:28
Cotigopro: 5−latek
Bo nie rozumiałem. Teraz już wiem. Dziękuje,
8 paź 20:29
Adamm: nie
8 paź 20:29
5-latek: Przeciez mozesz sobie podsatwic sam rozwiazania i sprawdzic
Po co CI 10 ludzi do tego ?
8 paź 20:30
Adamm: ale podpowiem ci : x musi być ≥0
8 paź 20:31
Mila:
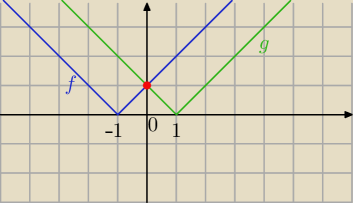
Jeszcze raz − teraz metoda graficzna.
|x+1|=|x−1|
f(x)=|x+1|
g(x)=|x−1|
8 paź 20:32
Cotigopro: Dziękuje Mila.
Mogłabyś mi wytłimaczyć to na jescze jednym przykładzie?
Oto on: |1−2x|+|2x−6|=x
Jak to rozwiązać, krok po kroku.
8 paź 20:35
Cotigopro: A tak btw. Jak nazywa się to co próbuje rozwiązać. Mam na myśli ten dział. Mam same zadania,
bez treści omawiających to.
Gdybyście mogli podać mi nazwę dziali, to poszukałbym w internecie poradnika i nauczyłbym się
szybciej.
8 paź 20:37
Adamm: metoda przedziałowa
| | 1 | | 1 | |
1−2x≥0 → |
| >x, 1−2x<0 → x> |
| |
| | 2 | | 2 | |
2x−6≥0 → x≥3, → 2x−6<0 → x<3
wybierasz odpowiednie przedziały (powinny być 3) i lecisz po wszystkich przypadkach
8 paź 20:39
Adamm: równania z wartością bezwględną
8 paź 20:39
5-latek: To co probujesz rozwiazac to jest rownanie
Dzial . Liczby rzeczywiste
8 paź 20:40
8 paź 20:41
Mila:
|1−2x|+|2x−6|=x⇔
|2x−1|+|2x−6|=x
lewa strona nieujemna to x≥0
Rozważamy :
|2x−6|=2x−6 dla x≥3
1
o
wtedy mamy równanie:
−2x+1−2x+6=0
−4x=−7
2
o
| | 1 | |
x∊< |
| ,3) wtedy mamy równanie: |
| | 2 | |
2x−1−2x+6=x
3
o
x≥3
2x−1+2x−6=x
3x=7
Brak rozwiązań.
===========
8 paź 20:43
Cotigopro: Czemu zamieniłaś |1−2x| na |2x−1|, i jak to zrobiłaś?
Skąd wiesz, że dana strona jest nieujemna?
8 paź 20:47
Adamm: |−x|=|x|, własność wartości bezwględnej
a wiadomo że jest nieujemna ponieważ |x|≥0
8 paź 20:49
8 paź 20:51
Cotigopro:
|2x−1|=2x−1 dla x≥1/2
|2x−6|=2x−6 dla x≥3
Czemu x>= 1/2 lub x >= 3?
8 paź 20:52
Adamm: wejdź w ten link i sobie poczytaj, tam jest wszystko wyjaśnione
8 paź 20:54
Cotigopro: Ok, poprawcie mnie jeśli robie źle:
|4−2x|+|−x+3|=5 −x+3>=0
4−2x >= 0 −x>=−3
−2x>=−4 x <=3
x <= 2
xε(−nieskonczonosci, 2> xε(−nieskonczonosci, 3>
Teraz licze dla tych przedziałow?
8 paź 21:02
Adamm:
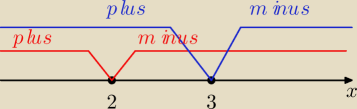
czerwony − 4−2x
niebieski − −x+3
8 paź 21:06
Cotigopro: Czyli mam 3przedzily?
(−nieskonczonosc, 2>
<2,3>
<3, nieskonczonosci)
?
8 paź 21:08
Cotigopro: Skoro tak, to gdzie zrobilem blad w obliczeniach?
8 paź 21:09
Adamm: nie wiem, ja tam widzę chaos
co do przedziałów to masz (−∞;2), <2;3>, (3;∞)
jeśli chodzi o przynależność 2, 3 do któregoś przedziału to to jest bez znaczenia
8 paź 21:10
Mila:
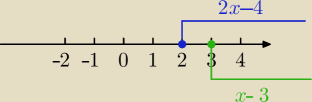
|4−2x|+|−x+3|=5
Dobrze jest przekształcić równanie do postaci:
|2x−4|+|x−3|=5
(korzystasz z własności|a|=|−a|)
1)
|2x−4|=2x−4 dla x≥2
|2x−4|=−2x+4 dla x<2
2)
|x−3|=x−3 dla x≥3
|x−3|=−x+3 dla x<3
Masz ilustrację przedziałów na osi liczbowej.
1)x<2 tu oba wyrażenia przyjmują wartości ujemne
2)x∊<2,3) tu jedno nieujemne a drugie ujemne
3) x∊<3,
∞).....
Teraz rozwiąż, sprawdzę.
8 paź 21:13
Cotigopro: Czyli powiniem rozwizać to tak:
przykład: |4−2x|+|−x−3|=5
|2x−4|+|x−3|=5
wtedy wychodzi, że
2x−4 >= 0
2x>=4
x>=2
Z drugim x−em wychodzi takze dobrze.
Można to tak przeksztalcic?
8 paź 21:13
Cotigopro: Spóźnilem się

8 paź 21:14
Cotigopro: Pierwsza częśc:
−2x+4−x+3=5
−3x=−2
x=2/3
8 paź 21:20
Mila:
Rozwiąż równanie.
8 paź 21:20
Cotigopro: Nie wiem Mila, o co chodzi z tym np. "dla x≥2".
Skąd to jest?
8 paź 21:22
Mila:
21:20 dobrze.
8 paź 21:24
Cotigopro: Ojjjjjej, ale jestem baran. Dobrze rozumiem, że dla n≥3 wyrażenie |x−3| będzie nieujemne?
Debilem jestem xd
8 paź 21:29
Mila:
Z definicji wartości bezwzględnej
|a|=a dla a≥0
|a|=−a dla a<0
zamiast "a" masz wyrażenie np.
|2x−4| więc, aby opuścić znak w. bezwzl. to badasz kiedy to wyrażenie 2x−4≥0 czyli
2x≥4⇔x≥2
Wtedy |2x−4|=2x−4
natomiast dla x<2 to wyrażenie przyjmuje wartości ujemne
np. x=1
2*1−4=−2
|−2|=−(−2)=2
|2x−4|=−2x+4
teraz gdy podstawisz 1 to masz tak:
−2*1+4=2
8 paź 21:30
Cotigopro: Chyba mam.
|4−2x|+|−x+3|=5
|2x−4|+|x−3|=5
2x−4=0 x−3=0
x=2 x=3
x∊(−inf;2>,(2;3>,(3,inf)
1.
x∊(−inf;2>
2x−4≤0, wiec |2x−4|=−2x+4
x−3<0, wiec |x−3|=−x+3
−2x+4−x+3=5
−3x+4=5
x=1 x∊(−inf;2>
2.x∊(2;3>
2x−4+x−3=5
3x=12
x=4
8 paź 21:51
Cotigopro: Dla trzeciego przedziału będzie tak samo jak dla drugiego?
8 paź 21:52
Mila:
Popraw (1) błąd w rachunkach
(2) źle ułożone równanie.
Patrz na oś liczbową, masz napisane, gdzie są dodatnie, dla reszty ujemne.
Pierwszy przedział
x∊(−∞,2)
drugi <2,3)
trzeci <3,∞)
8 paź 21:59
Mila:
Patrz na znaki wyrażeń, Adam napisał.
8 paź 22:02
Cotigopro: Czy to, jak beda zamkniete przedzialy ma duze znaczenie?
1.x∊(−inf;2>
2x−4≤0, wiec |2x−4|=−2x+4
x−3<0, wiec |x−3|=−x+3
−2x+4−x+3=5
−3x=−2
x=2/3 x∊(−inf;2>
8 paź 22:02
Mila:
(1) dobrze.
8 paź 22:10
Antonni: ja przepraszam Pani Milu ze sie wtracam w post ale niech kolega wytlumaczy mi to .
Z tego co wiem to infimum to to jest kres donlny zbioru i inf(a)=−∞
to co wobec tego oznacza −inf?
Bo to zadanie to jest 1 klasa liceum wiem bo ja tez powtarzam do matury i wedlug mnie
powinien byc zapis x∊(−∞,2)
8 paź 22:17
Cotigopro: 2.
|2x−4|≥0, wiec 2x−4
|x−3|≤, wiec −x+3
2x−4−x+3=5
x=6
Dobrze?
8 paź 22:21
Antonni: ja przepraszam ale to ja moze żle rozumuje .
tak to nalezy zapisywac ? . Bo juz teraz nie wiem
Chcialbym wobec tego dostac jednoznaczna odpowiedz . dziekuje .
8 paź 22:23
Cotigopro: "inf", jest skrótem od "infinity", czyli angielskiego słówka, które znaczy "nieskonczonosc".
Nie wiem gdzie esjte symbol odpowiedzialby za ilustracje teog pojęcia, więc uzyłem tego skrótu.
8 paź 22:24
Adamm: ∞
8 od lewej
8 paź 22:25
Cotigopro: AHahhaahhaha, rzeczywiście jest. Jestem więc ślepy i głupi

.
8 paź 22:26
Antonni: Widzisz kolego taki zapis moze mylic kogos kto chce skorzystac z tego postu
Wedlug mnie powinno sie pisac normalnie nieskon(−niesk) i wtedy kazdy wie o co chodzi
8 paź 22:29
Mila:
Antoni, masz rację.
Należy pisać (− ∞, 2) albo x<2.
8 paź 22:35
Cotigopro: 2.
|2x−4|≥0, wiec 2x−4
|x−3|≤, wiec −x+3
2x−4−x+3=5
x=6
Dobrze?
8 paź 22:36
Mila:
2)
x∊<2,3) dalej dobrze
....
x=6 nie należy do danego przedziału.
Teraz (3).
8 paź 22:38
Antonni: dziekuje za odpowiedz Pani Milu .
8 paź 22:39
Mila:

8 paź 22:41
Cotigopro: W 3. wynik będzie 4.
Dziękuje Mila, jesteś wielka. Najlepsza internetowa nauczycielka.
Dziękuje

8 paź 23:24
Mila:
(3) Dobrze.
Pracuj, a będą efekty. Powodzenia.

8 paź 23:28
 Jeszcze raz − teraz metoda graficzna.
|x+1|=|x−1|
f(x)=|x+1|
g(x)=|x−1|
Jeszcze raz − teraz metoda graficzna.
|x+1|=|x−1|
f(x)=|x+1|
g(x)=|x−1|
 czerwony − 4−2x
niebieski − −x+3
czerwony − 4−2x
niebieski − −x+3
 |4−2x|+|−x+3|=5
Dobrze jest przekształcić równanie do postaci:
|2x−4|+|x−3|=5
(korzystasz z własności|a|=|−a|)
1)
|2x−4|=2x−4 dla x≥2
|2x−4|=−2x+4 dla x<2
2)
|x−3|=x−3 dla x≥3
|x−3|=−x+3 dla x<3
Masz ilustrację przedziałów na osi liczbowej.
1)x<2 tu oba wyrażenia przyjmują wartości ujemne
2)x∊<2,3) tu jedno nieujemne a drugie ujemne
3) x∊<3,∞).....
Teraz rozwiąż, sprawdzę.
|4−2x|+|−x+3|=5
Dobrze jest przekształcić równanie do postaci:
|2x−4|+|x−3|=5
(korzystasz z własności|a|=|−a|)
1)
|2x−4|=2x−4 dla x≥2
|2x−4|=−2x+4 dla x<2
2)
|x−3|=x−3 dla x≥3
|x−3|=−x+3 dla x<3
Masz ilustrację przedziałów na osi liczbowej.
1)x<2 tu oba wyrażenia przyjmują wartości ujemne
2)x∊<2,3) tu jedno nieujemne a drugie ujemne
3) x∊<3,∞).....
Teraz rozwiąż, sprawdzę.

 .
.


