funkcja Fliniowa: Rozwiąz nierównosci metodą graficzna i alggebraiczna a)|x−3|< x+3 b) 1/2|x| − 3>=x c)|x| +2x>2 d)|x+1| +1>=x e)2|x−4|>=x−1 Prosze o jasne wytłumaczenie

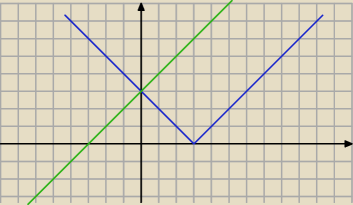
Qulka: a) |x−3| < x+3 niebieska < zielonej dla x >0

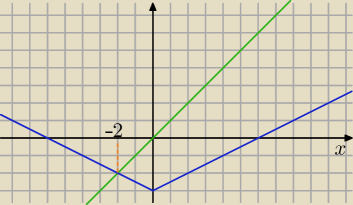
Qulka: b) 1/2|x| − 3 ≥ x niebieska ≥ zielonej dla x ≤ −2

grthx: Dobry wieczor Qulka Spojrz prosze na to . https://matematykaszkolna.pl/forum/331131.html dziekuje

grthx: a) |x−3|<x+3 x−3=0 to x=3 1 x∊(−∞,3) |x−3|=−(x−3)= −x+3= 3−x 3−x<x+3 −2x<0 x>0 w tym przedziale nie ma rozwiazan 2 x∊<3,∞) |x−3|= x−3 x−3<x+3 0<6 prawda Odp. Rozwiazaniem tej nierownosci jest przedzial x∊<3,∞)

grthx: Teraz poczekamy az sie autor postu odezwie i wtedy pomoc .

Qulka: z pierwszego przypadku x∊(0;3)

Fliniowa: Czyli jak mamy pod wartością bezwzględną to przyrównujemy zawsze do 0?

Fliniowa: dlaczego od −nieskończonosci do 3?

Qulka: bo https://matematykaszkolna.pl/strona/15.html

grthx: Jasne Qulka

Fliniowa: |x−3|=−(x−3)= −x+3= 3−x 3−x<x+3 −2x<0 x>0 w tym przedziale nie ma rozwiazan 2 x∊<3,∞) NIE ROZUMIEM WCALE TEGO

Fliniowa: HELP HELP

grthx: Przeciez masz napisane ze w tym przedziale jest rozwiazanie (byla poprawka ) bo w przedziale (−∞,3) liczby >0 to liczby ktore naleza do przedzialu (0,3) . Reszte sobie doczytaj