Rownania kwadratowe z parametrem
jamm: Dla jakich k równanie ma ujemne rozwiązania (k−2)x2 −(k+1)x−k=0
nie ogarniam jak to zrobić
4 wrz 15:57
grthx: dla k=2 równanie liniowe wyznacz x i ma być <0
dla k roznego od 2 masz rownanie kwadratowe
delta >=0
x1+x2<0
x1*x2>0 wzory wieta
4 wrz 16:03
===:
Δ≥0
xw<0
f(0) w zależności od (k−2)
4 wrz 16:03
jamm: Delta mi wyjdzie K2+6k−7 i z tego mam druga delte liczyc?
4 wrz 16:06
grthx: tak i >=0
4 wrz 16:08
Adamm: 2 rozwiązania? zakładam że ujemne jakiekolwiek
1. k−2=0, k=2
−3x−2=0
2. k≠2
Δ=(k+1)
2+k
2−2k=2k
2+1>0
drugi warunek
x
1*x
2<0 ∨ ( x
1*x
2>0 ∧ x
1+x
2<0 )
| | −k | |
dla x1*x2<0 mamy |
| <0, k(k−2)>0 |
| | k−2 | |
k∊(−
∞;0)∪(2;
∞)
dla x
1*x
2>0 mamy x∊(0;2)
| | k+1 | |
dla x1+x2<0 mamy |
| <0, (k+1)(k−2)<0 |
| | k−2 | |
k∊[(−1;2)∩(0;2)]∪(−
∞;0)∪(2;
∞)
k∊R
4 wrz 16:09
jamm: wyszły mi miejsca zerowe −7 i 1 i co dalej z tym?
4 wrz 16:11
Adamm: ah przepraszam Δ=(k+1)2+4k2−8k=5k2−6k+1=(5k−1)(k−1)≥0,
k∊(−∞;1/5>∪<1;∞)
4 wrz 16:13
jamm: dalej nie ogarniam o co tu chodzi

4 wrz 16:14
Adamm: 1. źle policzyłeś deltę
2. sprawdzamy dla liniowego
3. liczymy deltę (musi istnieć taki x że f(x)=0)
4. wzorami vieta sprawdzamy znaki x1, x2
4 wrz 16:15
jamm: delta będzie (k+1)2 − 4*(k−2)*−k
4 wrz 16:17
Adamm: (k+1)2 − 4*(k−2)*(−k)=k2+2k+1+4(k2−2k)=5k2−6k+1
4 wrz 16:21
grthx: A dlaczego dales warunek x1*x2<0 przecież tutaj musi być jedno rozwiązanie dodatnie ?
4 wrz 16:24
jamm: a nie powinno być −k2+2k? po przemnożeniu (k−2) * (−k)?
4 wrz 16:24
Adamm: zauważ że (k+1)2−4(k−2)(−k)=k2+2k+1+4(k2−2k)
zmieniłem znak na dodatni
4 wrz 16:25
jamm: A dobra i jak oblicze że ta delta to 5k2−6k+1 >= 0 to co z tym dalej sie robi? Kolejną delte
liczy tak?
4 wrz 16:27
Adamm: tak, rozwiązania k1 i k2
4 wrz 16:29
Adamm: wstawić to do postaci (k−k1)(k−k2)≥0
4 wrz 16:29
Adamm:
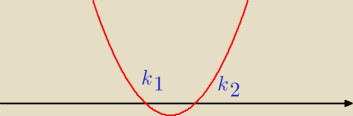
4 wrz 16:30
jamm: Ok mam że 1 i 1/5 a jeszcze pytanie co do przedziałów mam bo nwm kiedy tu bedą otwarte a kiedy
zamkniete
4 wrz 16:31
jamm: masz może jakieś gg i chilwe żeby mi to lepiej wytlumaczyc czy coś?
4 wrz 16:34
Adamm:
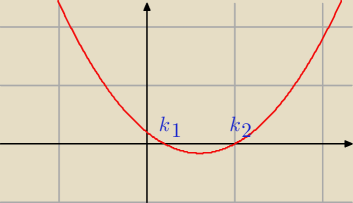
czyli inaczej (k−1/5)(k−1)≥0
funkcja ma ramiona skierowane do góry, 0 jest osią x
4 wrz 16:50
Adamm: nierówność zachodzi kiedy funkcja przecina lub jest ponad osią x
4 wrz 16:51
Adamm: po co mi GG

poza tym, mamy to forum, nic więcej nie trzeba
4 wrz 16:53
jamm: no mam przedział że k należy do k∊(−∞;1/5>∪<1;∞) ale to mam tylko to z delty i że k=/2 ze
wzgledu ze a nie równa się 0
4 wrz 16:57
jamm: i nie wiem teraz co z tymi viete'a i tu chyba jeszcze trzeba z liniową zrobić
4 wrz 16:57
4 wrz 16:57
4 wrz 16:58
jamm: mam te zależność że x1*x2>0 a z tych vietea jest że x1*x2 to c/a czyli mam że
k
−−− >0
k−2
4 wrz 16:59
jamm: znaczy
−k
−−− >0
k−2
4 wrz 16:59
Adamm: jeśli chodzi o liniowość to zakładasz że współczynnik przy największej potędze =0,
dla ≠0 masz funkcję kwadratową
4 wrz 16:59
Adamm: | f(x) | |
| >0 ∧ g(x)≠0, ⇒ f(x)*g(x)>0 |
| g(x) | |
4 wrz 17:01
Adamm: założenie x1*x2>0 jest niewystarczające powinno być jeszcze x1+x2<0
4 wrz 17:03
jamm: a te x1 i x2 brać z c/a czy brać te 1 i 1/5 co obliczylem z delty delty?
4 wrz 17:08
Adamm: c/a ...
4 wrz 17:09


 czyli inaczej (k−1/5)(k−1)≥0
funkcja ma ramiona skierowane do góry, 0 jest osią x
czyli inaczej (k−1/5)(k−1)≥0
funkcja ma ramiona skierowane do góry, 0 jest osią x
 poza tym, mamy to forum, nic więcej nie trzeba
poza tym, mamy to forum, nic więcej nie trzeba