Całki zadanie tekstowe zef: Chciałem spróbować zadanie z całkami gdzie należy obliczyć jakieś pole. Mam zadanie ze starej książki: Oblicz pole figury F, jeśli:

	1		−x2+10
F={(x,y):		≤y≤		i x∊R\{0} }
	x2		9

Zaczynam od znalezienia miejsca przecięcia tych funkcji ( to będą moje granice całkowania ) y1=y2

1		−x2+10
	=		, x≠0
x2		9

9=−x⁴+10x² x²=t, t>0 −t²+10t−9=0 t1=9 t2=1 czyli x1=1 lub −1 x2=3 lub −3 Wybieram granice całkowania 1 i 3 Zapisuję to jako:

	−x2+10		1
F=13∫		dx−13∫		dx
	9		x2

Zajmę się najpierw obliczeniem całek nieoznaczonych, zacznę od pierwszej

	−x2+10		−x2		10		1		10
∫		dx=∫		dx+∫		dx=−		∫x2dx+		x=
	9		9		9		9		9

	1		x3		10		−x3		10		−x3		30x
−		*		+		x=		+		x=		+		=
	9		3		9		27		9		27		27

x(−x2+30)
27

____________ Druga całka nieoznaczona:

	1		x−1		1
∫		dx=∫x−2dx=		=−x−1=−
	x2		−1		x

__________________________________________ Liczę pierwszą całkę oznaczoną: 3 | |

	x(−x2+30)		3(21)		1(29)		34
|		| =		−		=
	27		27		27		27

| | 1 Liczę drugą całkę oznaczoną: 3 | |

	1		1		1		2		18
|−		| = −		−(−		)=		=
	x		3		1		3		27

| | 1 odejmuję wyniki z 2 całek oznaczonych

34		18		16
	−		=
27		27		27

Takie wyszło mi pole jednego z obszarów jednak teraz nie wiem czy nie powinienem tego przemnożyć przez 2 ze względu na ta że mogłem całkować także mając granice −1 i −3 Mógłby ktoś sprawdzić te zadanie ?

daras: chciałes czy ci kazali ?

zef: Chciałem, znalazłem w domu starą książkę i takie zadanie w niej było

daras: to sie porzadnie zaloguj i wtedy może będę ci w stanie pomóc

piotr1973: Dobry wynik dla pola dla x>0 https://www.wolframalpha.com/input/?i=int+(-x%5E2%2B10)%2F9-1%2Fx%5E2+from+1+to+3 https://www.wolframalpha.com/input/?i=1%2Fx%5E2%3D(-x%5E2%2B10)%2F9

zef: Czyli trzeba przemnożyć to razy 2 czy nie ? Bo przecież będą 2 pola, może ktoś sprawdzić całe zadanie nie tylko wynik ?

Mariusz: Dziwne że zabiera się za całki oznaczone bez przećwiczenia nieoznaczonych

zef: Nieoznaczonych już trochę ćwiczyłem i coś już wiedzy o nich mam . Z resztą sam wiesz ile umiem

zef: Przez cały sierpień byłem w pracy i nie miałem czasu aby kontynuować naukę dot. całek nieoznaczonych

Mariusz: Wg mnie za mało Mieliśmy przećwiczyć ten jeden przypadek całek z funkcji wymiernych i przejść do podstawień to przestałeś reagować na wpisy

zef: W swoich postach piszesz bardzo dużo teorii która jest dla mnie trudna do zrozumienia, dużo schematów, mało przykładów. Łatwiej wchodzi mi wiedza kiedy widzę to na konkretnych przykładach bo te rzeczy które piszesz rozumieją pewnie studenci, którzy mają już więcej wiedzy.

Mariusz: Całki z funkcji wymiernych to głównie liniowość całki poza tym jest na nie schemacik do którego przydają się podstawy algebry liniowej Wiele podstawień sprowadza całki do całek z funkcji wymiernych więc chciałem abyś je najpierw przećwiczył zanim przejdziesz do podstawień a później oznaczonych tych właściwych i niewłaściwych a darasy ci nie pomogą bo to głównie spamery są Przy obliczaniu pól pod krzywą , długości krzywych , pól powierzchni i objętości brył obrotowych przydaje się parametryzacja albo przejście na inne współrzędne np długość kardioidy najlepiej liczy się na współrzędnych biegunowych a długość asteroidy korzystając z równania parametrycznego

Mariusz: Oblicz długość paraboli y=x² na odcinku (0,1) (y')=2x (y')²=4x² ∫₀¹√1+4x²dx Współczynnik przy x² jest dodatni więc stosujesz podstawienie √1+4x²=t−2x 1+4x²=t²−4xt+4x² 1=t²−4xt 4xt=t²−1

	t2−1
x=
	4t

	4t2−2t2+2		t2+1
√1+4x2=t−2x=		=
	4t		2t

	2t*4t−4(t2−1)
dx=		dt
	16t2

	t2+1
dx=		dt
	4t2

	t2+1	t2+1
∫			dt
	2t	4t2

	1		(t2+1)2
=		∫		dt
	8		t3

	1		t4+2t2+1
=		∫		dt
	8		t3

	1		dt		dt
=		(∫tdt+∫		+2∫		)
	8		t3		t

	1		t2		1
=		(		−		+2ln|t|)+C
	8		2		2t2

	1		t4−1
=		(		+2ln|t|)+C
	8		2t2

	1		t4−1
=		(		+ln|t|)+C
	4		4t2

	1		t2−1	t2+1
=		(			+ln|t|)+C
	4		2t	2t

	1
=		(2x√1+4x2+ln|2x+√1+4x2|)+C
	4

	1		1
∫01√1+4x2dx=		(2√5+ln|2+√5|)−		(0+0)
	4		4

	1
∫01√1+4x2dx=		(2√5+ln(2+√5))
	4

zef: Rozumiem to co napisałeś, mam tylko jedno pytanie skąd wzięło się te 1 dx=... bo te drugie to po skróceniu jest, to wiem.

zef: Dobra już wiem, wzięło się to z linijki wyżej w t−2x podstawiłeś po prostu x, możesz mi dać jakiś przykład i wzorując się na tym go rozwiążę

Mariusz: Oblicz pole ćwiartki koła o promieniu jednostkowym x²+y²=1 y²=1−x² y=√1−x² ∫₀¹√1−x²dx Tutaj współczynnik przy x² masz ujemny więc trójmian kwadratowy zapisujesz w postaci iloczynowej i podstawiasz √(1−x)(1+x)=(1+x)t (1−x)(1+x)=(1+x)²t² 1−x=(1+x)t² 1−x=t²+xt² 1−t²=x+xt² 1−t²=x(1+t²)

	1−t2		2
x=		=−1+
	1+t2		1+t2

	2t
√(1−x)(1+x)=(1+x)t=
	1+t2

dx=2*(−1)*(1+t²)⁻²*2tdt

	4t
dx=−		dt
	(1+t2)2

	2t		4t
∫		(−		dt)
	1+t2		(1+t2)2

	−8t2
=∫		dt
	(1+t2)3

	−8t2		a3t3+a2t2+a1t+a0		b1t+b0
∫		dt=		+∫		dt
	(1+t2)3		(1+t2)2		1+t2

−8t2		(3a3t2+2a2t+a1)(1+t2)2
	dt=
(1+t2)3		(1+t2)4

	(a3t3+a2t2+a1t+a0)(1+t2)*4t		b1t+b0
−		+
	(1+t2)4		1+t2

−8t2		(3a3t2+2a2t+a1)(1+t2)
	dt=
(1+t2)3		(1+t2)3

	4t(a3t3+a2t2+a1t+a0)		(b1t+b0)(1+t2)2
−		+
	(1+t2)4		(1+t2)3

−8t²=(3a₃t²+2a₂t+a₁)(1+t²)−4t(a₃t³+a₂t²+a₁t+a₀) +(b₁t+b₀)(t⁴+2t²+1) −8t²=(3a₃t⁴+2a₂t³+a₁t²+3a₃t²+2a₂t+a₁)− (4a₃t⁴+4a₂t³+4a₁t²+4a₀t)+(b₁t⁵+2b₁t³+b₁t+b₀t⁴+2b₀t²+b₀) −8t²=b₁t⁵+(b₀−a₃)t⁴+(2b₁−2a₂)t³+(2b₀+3a₃−3a₁)t² +(b₁+2a₂−4a₀)t+b₀+a₁ b₁=0 b₀−a₃=0 2b₁−2a₂=0 2b₀+3a₃−3a₁=−8 b₁+2a₂−4a₀=0 b₀+a₁=0 b₁=0 b₀=a₃ a₂=0 a₀=0 5a₃−3a₁=−8 a₁=−a₃ b₁=0 b₀=a₃ a₂=0 a₀=0 8a₃=−8 a₁=−a₃ b₁=0 b₀=−1 a₃=−1 a₂=0 a₁=1 a₀=0

	−8t2		−t3+t
∫		dt=		−arctan(t)+C
	(1+t2)3		(1+t2)2

	−8t2		t	1−t2
∫		dt=			−arctan(t)+C
	(1+t2)3		1+t2	(1+t2)

	1		√1−x2
∫√1−x2dx=		x√1−x2−arctan(		)
	2		1+x

	π		π
∫01√1−x2dx=(0−0)−(0−		)=
	4		4

Na marginesie dodam że akurat tę całkę znacznie lepiej liczyłoby się przez części ale chciałem ci pokazać jakiego podstawienia możesz użyć gdy współczynnik przy x² jest ujemny Zastanowię się nad przykładem dla ciebie

Mariusz: Oblicz pole powierzchni elipsoidy obrotowej o promieniach a=6378 , b=6357

zef: Liczyłem bardziej na zadanie typu oblicz długość paraboli na jakimś odcinku, ponieważ już jedno takie rozwiązałeś i miałbym się na czym wzorować, z elipsoidą nawet nie wiem jak się zabrać

Mariusz: Poznajesz te promienie ?

x2		y2
	+		=1 równanie elipsy
a2		b2

P=2π∫_x1^x₂y√1+(y')²dx Oblicz długość paraboli y=x²+2x+5 na przedziale (0,2)

zef: nie znałem nawet tego równania elipsy Liczę długość paraboli na przedziale 0,2 f(x)=x²+2x+5 f'(x)=2x+2 [f'(x)]²=4x²+8x+4 ₀²∫√4x²+8x+4dx √4x²+8x+4=t−2x 4x²+8x+4=t²−4xt+4x² 8x+4=t²−4xt 8x+4xt=t²−4 x(8+4t)=t²−4

	t2−4
x=
	8+4t

	2t2−8		t(8+4t)		2t2−8
√4x2+8x+4=t−2x=t−		=		−		=
	8+4t		8+4t		8+4t

4t2+8t		2t2−8		2t2+8t+8
	−		=
8+4t		8+4t		8+4t

Hmm doszedłem do czegoś takiego, nie wiem czy to jest dobrze

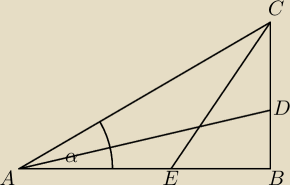
Mariusz: Nie dodałeś jedynki , wzorek jest taki ∫_a^b√1+[f'(x)]²dx Rozbijasz przedział na podprzedziały z twierdzenia Pitagorasa obliczasz przekątną i liczysz granicę sumy tych przekątnych na podprzedziałach Mniej więcej stąd się ten wzorek wziął Pamiętasz to zadane z trójkątem prostokątnym , dwusiecznymi kątów ostrych i stosunkami boków ? Jest przydatne gdybyś tych podstawień zapomniał Jak znasz rosyjski to mogę ci podesłać geometryczną interpretację tych podstawień To zadanie z trójkątem wyglądało mniej więcej tak W trójkącie ABD interesują nas stosunki

DB
BA

AB
BD

W trójkącie CBE interesują nas stosunki

EB
BC

CB
BE

Długości AB , BC, CA dobierasz tak aby z twierdzenia Pitagorasa otrzymać √a²−x² albo √a²+x² albo √x²+a²

Mariusz: * albo √x²−a²

Mariusz: Z darmowych e−książek jesteś ograniczony do tej http://matwbn-old.icm.edu.pl/kstresc.php?tom=15&wyd=10&jez=pl i do tej http://kielich.amu.edu.pl/Stefan_Banach/rachunek.html (całki są w drugim tomie)

Mariusz: Сборник задач по математическому анализу. Jeśli chcesz zbioru zadań to daj takie zapytanie a może coś znajdziesz

Krzysiek58: Mariusz zef chce sie nauczyc tylko rozwiazywania calek . On i tak nie bedzie czytal tego Kuratowskiego czy Banacha tym bardziej Fichtenholza Nauczy sie rozwiazywac pare typow calek i to wystarczy Polecam .Metody rozwiazywania calek Obczynski .

Mariusz: Krzysiek podałem mu darmowe pozycje gdyby jednak chciał sobie poczytać Poza tym ja taką analizę jaką podaje Kuratowski miałem jeszcze w średniej

Krzysiek58: Mariusz tylko nielicznym chce sie teraz czytac ksiazki Z drugiej strony tak jak piszesz duzo wiadomosci bylo przedtem w sredniej i przystepujac np do czytania Lei czy Kuratowskiegi , Sikorskiego student wiedzial o czym czyta . Nie mowiac juz o 3 tomowym Fichtenholzie .

Mariusz: Fichtenholz czy Leja był dla pierwszego roku studiów Przejrzawszy Kuratowskiego wydaje mi się że dla licealisty jest odpowiedni

daras: masz racje Krzysiu, większość jak znajdzie jakis problem, istotny czy tez nie, to zaraz pisza na forum i czekają aż stara gwardia im to w try miga rozwiąże po czym równie szybko o tym zapominają

Mila: 1)

	x2		x
Oblicz pole figury ograniczonej łukiem krzywej y=		−		−2 oraz osią OX
	4		2

2) Oblicz pole figury ograniczonej łukiem krzywej y=(x+2)³, osią OX oraz osią OY. 3) Oblicz pole figury ograniczonej łukami krzywych y=x²,y=x²+2 oraz prostymi x=1 i x=3. 4) Oblicz pole figury ograniczonej krzywymi y=x² i y²=x

daras: l'arte pour l'arte

piotr: http://www.alleng.ru/d/math/math20.htm

piotr: https://archive.org/details/problemsinmathem031405mbp

zef: f(x)=x²+2x+5 f'(x)=2x+2 [f'(x)]²=4x²+8x+4 √1+4x²+8x+4=t−2x /² 4x²+8x+5=t²−4xt+4x² 8x+4xt=t²−5 x(8+4t)=t²−5

	t2−5
x=
	8+4t

	4t2+8t−(2(t2−5))		2t2+8t+10		t2+4t+5
√4x2+8x+5=t−2x=		=		=
	8+4t		8+4t		4+2t

Znowu zatrzymałem się w tym momencie

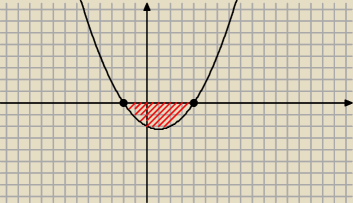
zef: Zadania od Mila: 1)y1=1/4x²−1/2x−2 y2=0 − ograniczenie przez osi ox y1=y2 liczę pierwiastki równania z delty: 4 i −2 ₋₂⁴∫0,25x²−0,5x−2dx

	x3
1/4∫x2dx=		+C
	12

	x2
−1/2∫xdx=−		+C
	4

∫−2dx=−2x+C liczę górną granice:

16		16		36		−20
	−4−8=		−		=
3		3		3		3

dolna:

	9
−3/4−1+4=
	4

−20		9
	−		= wyjdzie na pewno coś ujemnego więc albo się gdzieś pomyliłem albo trzeba dać
3		4

jakoś wartość bezwzględna albo może podmienić znaki ?

Mariusz: Obszar którego liczysz pole znajduje się pod osią OX więc nic dziwnego że całka wychodzi ujemna Jeśli liczysz pole obszaru ograniczonego krzywymi to możesz skorzystać ze wzoru ∫(y₂(x)−y₁(x))dx Mila podasz przykład gdzie wygodniej jest zastosować równanie parametryczne krzywej albo przejść na inny układ współrzędnych np biegunowy

Mariusz: Co do całki z 30 sierpnia 17:27 to teraz wystarczy zróżniczkować x po t i wstawić do całki Przyda się także przedstawić licznik w postaci sumy potęg dwumianu t+2 bo po skorzystaniu z liniowości całki licznik poskraca się z mianownikiem (można to zrobić stosując kilkukrotnie schemat Hornera)

Mila: 1)

	1		1
−2∫4[0−(		x2−		x−2)] dx=
	4		2

	1		1
=−2∫4[−		x2+		x+2)] dx=
	4		2

	1		1
=[−		x3+		x2+2x]−24=
	12		4

	1		1		1		1
=−		*43+		*42+2*4−[−		*(−2)3+		*(−2)2+2*(−2)]=...
	12		4		12		4

=9

Mila: Licz następne.

zef:

	t2−5		2t(8+4t)−(t2−5)(4)		8t2+16t−4t2+20
dx=		d/dt=		=		=
	8+4t		(8+4t)2		(8+4t)2

4t2+16t+20		t2+4t+5
	=
64+64t+16t2		4t2+16t+16

	t2+4t+5		t2+4t+5
∫		*		dt=
	4t2+16t+16		4+2t

	(t2+4t+5)2
∫		dt
	(4+2t)3

	t4+8t3+26t2+40t+25
∫		dt
	8t3+52t2+96t+64

dzielę przez siebie licznik i mianownik

	1		3		17   t2+14t+13 4
∫		t+		dt +∫		dt=
	8		16		8t3+48t2+96t+64

t2		3		17   t2+14t+13 4
	+		t+∫		dt
16		16		8t3+48t2+96t+64

	17   t2+14t+13 4
∫		dt=
	8t3+52t2+96t+64

v=8t³+52t²+96t+64 v'=24t²+104t+96

	17   t2+14t+13 4
∫		dt=
	(4+2t)3

17   t2+14t+13 4		A		B		C
	=		+		+
(4+2t)3		4+2t		(4+2t)2		(4+2t)3

17
	t2+14t+13=A(4+2t)2+b(4+2t)+C
4

17
	t2+14t+13=A(16+16t+4t2)+4B+2Bt+C
4

17
	t2+14t+13=16A+16At+4At2+4B+2Bt+C
4

17
	t2+14t+13=t2(4A)+t(16A+2B)+16A+4B+C
4

	17
4A=
	4

	17
A=
	18

16A+2B=14

	20
2B=−
	18

	−20
B=
	36

16A+4B+C=13

272		40		234
	−		−		=−C
18		18		18

	1
C=
	9

	17   18		20   36		1   9
∫		dt−∫		dt+∫		dt
	4+2t		(4+2t)2		(4+2t)3

To jest reszta z wielomianu, czy do tego momentu jest dobrze ?

jc: zef, czego dotyczy ten straszny rachunek?

zef: kontynuacja całki z 30 sierpnia 17:27, polecenie obliczyć długość krzywej granice 0,2

Mariusz: Zef nie skorzystałeś z mojej podpowiedzi t⁴+8t³+26t²+40t+25 − zakładam że to dobrze policzyłeś 1 8 26 40 25 −2 1 6 14 12 1 −2 1 4 6 0 −2 1 2 2 −2 1 0 −2 1 (t+2)⁴−2(t+2)²+1=t⁴+8t³+26t²+40t+25 Tutaj akurat można było skorzystać ze wzory skróconego mnożenia

Mariusz: * ma być (t+2)⁴+2(t+2)²+1

jc: Proponuję coś podobnego. Obliczyć długość wykresu y = 2√x, 0 ≤ x ≤ 9/16.

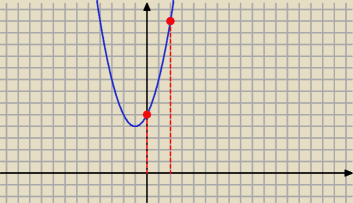
Mila: f(x)=x²+2x+5 f'(x)=2x+2=2*(x+1) L=₀∫²√1+4*(x+1)² dx=

	1		1
[x+1=		t, dx=		dt]
	2		2

cd.

	1
=		*0∫2√1+t2dt= taką całkę masz we wzorach.
	2

Mariusz: a coś gdzie przydatne są równania parametryczne krzywej albo zmiana układu współrzędnych Przykładowo pole i długość asteroidy lepiej obliczyć używając parametrycznego równania tej krzywej a pole i długość kardioidy lepiej obliczyć stosując układ współrzędnych biegunowych

Mila: Mariusz, to już bardziej zaawansowana wiedza, a zef chyba początkujący? Jestem zwolenniczką stopniowania trudności w nauce.

Mariusz: ok też uważam to za dobry pomysł tylko myślałem że już można

Mariusz: Uważam też że za szybko wziął się za całki oznaczone Powinien więcej poćwiczyć całki nieoznaczone Całkowanie funkcji wymiernych

	L(x)
∫		dx
	M(x)

Rozważamy trzy przypadki 1. deg L(x)≥ deg M(x) L(x)=W(x)M(x)+R(x)

	L(x)		R(x)
∫		dx=∫W(x)dx+∫		dx
	M(x)		M(x)

2. deg R(x)< deg M(x) ⋀ gcd(M(x),M'(x))≠const

	R(x)		R1(x)		R2(x)
∫		dx=		+∫		dx
	M(x)		M1(x)		M2(x)

M₁(x)=gcd(M(x),M'(x)) M(x)=M₁(x)M₂(x) deg R₁(x)< deg M₁(x) deg R₂(x)< deg M₂(x) Liczniki R₁(x) oraz R₂(x) obliczamy metodą współczynników nieoznaczonych Za współczynniki tych wielomianów przyjmujemy współczynniki literowe i różniczkujemy powyższą równość aby te współczynniki obliczyć 3. deg R(x)< deg M(x) ⋀ gcd(M(x),M'(x))=const

	R2(x)
∫		dx
	M2(x)

Niech M₂(x)=(x−a₁)(x−a₂)*...*(x−a_k) (x²+p₁x+q₁)(x²+p₂x+q₂)*...*(x²+p_mx+q_m)

	R2(x)		A1		A2		Ak
∫		dx=∫		dx+∫		dx+...+∫		dx
	M2(x)		x−a1		x−a2		x−ak

	B1x+C1		B2x+C2
+∫		dx+∫		dx
	x2+p1x+q1		x2+p2x+q2

	Bmx+Cm
+...+∫		dx
	x2+pmx+qm

	Bx+C
Całkę ∫		dx można policzyć w ten sposób
	x2+px+q

	Bx+C		1	B(2x+p)+(2C−Bp)
∫		dx=			dx
	x2+px+q		2	x2+px+q

	Bx+C		B		2x+p		2C−Bp		dx
∫		dx=		∫		dx+		∫
	x2+px+q		2		x2+px+q		2		x2+px+q

Do pierwszej całki można pomocniczo zastosować podstawienie t=x²+px+q

	p		p2
Do drugiej całki można pomocniczo zastosować podstawienie (x+		)2=(q−		)t2
	2		4

Całki zawierające pierwiastek z trójmianu kwadratowego Tutaj mamy trzy podstawienia z których wystarczyłyby tylko dwa ∫R(x,√ax²+bx+c)dx − R(x,y) funkcja wymierna dwóch zmiennych 1. a>0 Stosujemy podstawienie √ax²+bx+c=t−√ax Obliczamy x z podstawienia Różniczkujemy obustronnie W razie potrzeby obliczamy pierwiastek 2. a<0 Tutaj możemy założyć że b²−4ac>0 w przeciwnym razie trójmian kwadratowy przyjmowałby stale wartości ujemne Stosujemy podstawienie √ax²+bx+c=(x−x₁)t Gdzie x₁ jest jednym z pierwiastków trójmianu kwadratowego Dalej postępujemy podobnie jak w przypadku gdy a>0 Całka z różniczki dwumiennej ∫x^m(a+bxⁿ)^pdx Tutaj rozważamy trzy przypadki z których jeden nie wymaga podstawienia chyba że koniecznie chcemy mieć całkę z funkcji wymiernej 1. p∊ℤ

	m+1
2.		∊ℤ
	n

	m+1
3.		+p∊ℤ
	n

Całki ∫R(e^x)dx Tutaj podstawienie samo się narzuca Do tych całek można sprowadzić całki z hiperbolicusami ∫R(sinh(x),cosh(x))dx Całki ∫R(sin(x),cos(x))dx

	x
Tutaj sprawdza się podstawienie t=tan(		)
	2

Argument tangensa można równie dobrze przesunąć

	x
tzn zamiast podstawienia t=tan(		)
	2

	x
można równie dobrze zastosować podstawienie t=tan(		+φ)
	2

gdzie φ=const

Mariusz: Algebra przydaje się do całkowania funkcji wymiernych gdyż je liczymy korzystając głównie z liniowości całki Przydaje się także do metody współczynników nieoznaczonych jak ktoś ją lubi Później przyda się do przekształcenia Laplace wszak przekształcenie Laplace to właśnie całka oznaczona (niewłaściwa) oraz do rozwiązywania uładów równań różniczkowych Teraz jednak algebra przydaje się głównie do całkowania funkcji wymiernych Oto co z algebry się przydaje Operacje na wielomianach dodawanie i odejmowanie mnożenie i dzielenie z resztą NWD wielomianu − algorytm brania reszt z kolejnych dzieleń jeżeli jednak mamy dany rozkład wielomianu na czynniki to możemy go wykorzystać rozkład wielomianu na czynniki liniowe i kwadratowe nierozkładalne nad R − do stopnia czwartego włącznie rozkład taki jest względnie łatwy i nie wymaga stosowania funkcji nieelementarnych Operacje na macierzach dodawanie , odejmowanie ,mnożenie eliminacja Gaussa wyznacznik macierzy macierz odwrotna i rozkład macierzy np LU Rozwiązywanie układów równań liniowych Tutaj mamy wzory wyznacznikowe Cramera czy eliminację Gaussa chociaż macierz odwrotna oraz rozkład LU mają taką zaletę że jak już raz się je znajdzie to później łatwo rozwiązywać układy równań różniące się tylko kolumną wyrazów wolnych Do układów równań różniczkowych przydadzą się również wartości i wektory własne diagonalizacja i postać Jordana macierzy exponenta macierzy Ty jednak na razie nie będziesz się tym zajmował

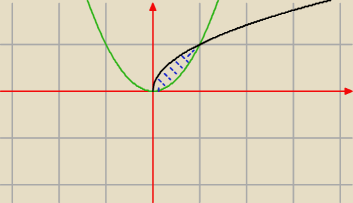
zef: Zajmę się teraz zadaniem czwartym bo wygląda na możliwe do rozwiązania y=x² y²=x −> y=√x −> zał. x≥0 y1=y2 x²=√x x²−√x=0 √x=t t⁴−t=0 t(t³−1)=0 t=0 lub t=1 √x=0 √x=1 x=0 lub x=1 To są nasze granice, widać je na rysunku liczę to ze wzoru na różnicę tych funkcji w całce oznaczonej ₀¹∫x²−√xdx I nie mam pomysłu na tą całkę

zef: Ciągle myślałem że tam jest znak mnożenia a nie minus ! Już kończę tę całkę !

zef:

	x3		2x3/2		x3−2x3/2		1−2√1
= |		−		|10=		=		Dziwny wynik mi wyszedł
	3		3		3		3

piotr1973: funkcja podcałkowa powinna być taka: √x−x² gdy przestawiłeś kolejność wyszło pole ujemne

zef: w jaki sposób ustawiać kolejność odejmowania ?

Benny: Masz funkcje f₁ i f₂. Sprawdzasz która jest nad którą. np. f₁ jest nad f₂, więc robisz f₁−f₂

zef:

	2x3/2		x3		2x3/2−x3		2−1		1
01∫√x−x2dx=		−		=		=		=
	3		3		3		3		3

Teraz powinno się zgadzać

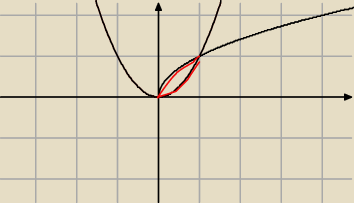
zef: Chodzi o te czerwone części tych funkcji i która część znajduje się wyżej to zaczynam od niej odejmować funkcję której zaznaczony kawałek jest niżej tak ?

Benny: Tak

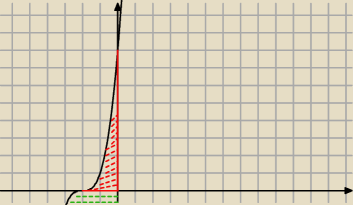
zef: Zad 3 Oblicz pole figury ograniczonej łukiem krzywej y=(x+2)³, osią OX oraz osią OY. Czyli figura ograniczona przez: y=0 x=0 y=(x+2)³ y1=y2 (x+2)³=0 x=−2 jedna granica druga powinna wynosić 0 Ale tutaj nie wiem czy nie powinienem zrobić dodatkowego założenia odnośnie jeszcze tego że y=0 ogranicza to pole Bo chyba gdyby nie te ograniczenie to pole byłoby jeszcze niżej (zielone linie) ∫₋₂⁰(x+2)³dx

piotr1973: oś OX ma równanie y=0, więc to założenie jest zbędne, gdyby w poleceniu pominąć oś OX było by ono niedookreślone,

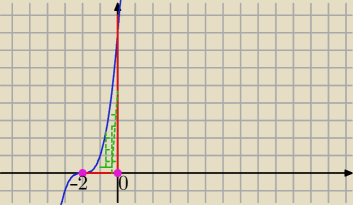
Mila: Zadanie 3. Od górnej f(x)=(x+2)³ odejmujesz dolną y=0 Pole zielonego obszaru {−2}∫⁰((x+2)³−0) dx= ∫((x+2)³dx=∫(x³+6x²+12x+8)dx=.. P=4 licz.

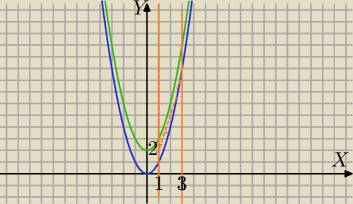
Mila: 3) Oblicz pole figury ograniczonej łukami krzywych y=x²,y=x²+2 oraz prostymi x=1 i x=3 ₁∫³(x²+2−x²) dx=₁∫³(2) dx=[2x]₁³=2*3−2*1=4

Mila: 9:37 dobrze.

Mila: zef , polecam. Analiza Gewert,Skoczylas. Masz wszystko pięknie wytłumaczone, po kolei. Ty zaczynasz od środka, początku nie ma , a koniec nie wychodzi. http://staff.uz.zgora.pl/jskowron/pliki/MPT3.pdf

zef: Zad ∫₋₂⁰((x+2)³−0)dx= ∫₋₂⁰x³+6x²+12x+8dx=

	x4
|		+2x3+6x2+8x|−20
	4

0−(4−16+24−16)=0−(−4)=4 Wyszło dobrze Biorę się za kolejne, już ostatnie zadanie

zef: Aj, nie zauważyłem, że zrobiłaś je w poście o 16:19, masz może jeszcze jakieś podobne zadania ?

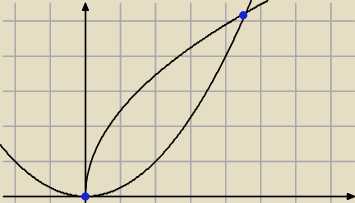
zef: Znalazłem sam jedno zadanie z tej samej książki: oblicz pole figury ograniczonej łukami dwóch parabol:

	1
y=		x2 i y2=6x
	4

	1
y=		x2
	4

y²=6x −> y=√6x 6x≥0, x≥0 √6x=0,25x²

1
	x2−√6√x=0
4

x^0,5=t t≥0

1
	t4−√6t=0
4

	1
t(		t3−√6)=0
	4

	1
t=0 lub		t3=√6
	4

x=0 t³=4√6 x^3/2=4√6 /² x³=96 x=2³√12

	1
023√12∫√6x−		x2dx
	4

	1
023√12∫√6*x0,5−		x2dx
	4

2√6x3/2		x3
	−
3		12

4√72		24
	−
3		12

24√2		24
	−
3		12

24√2−6
3

Odpowiedź to 8 a mi wyszedł taki wynik, znajdzie mi ktoś błąd ?

jc: Błąd jest w trzeciej linii od dołu. Nie licz takich strasznych rzeczy. Od tego są komputery. Może jeszcze byłoby coś ciekawego w ogólnym rachunku: y=ax², x=by², 0 < a,b. W takim szczególnym nieciekawym przypadku nic nie ma No chyba że rzecz dotyczy jakiegoś ważnego problemu technicznego.

jc: Dużo łatwiej wykonać rachunki w ogólnym przypadku (y=ax², x=by²).

	2
Pole =
	3ab

U nas a = 1/4, b =1/6, Pole = 2*4*6/3 = 8.

Mila:

	2		x3
[		√6+√x3−		]023√12=
	3		12

	2		8*12
=		*√6*[(23√12)3]1/2−		=
	3		12

	2
=		*√6*√8*12−8=
	3

	2
=		*√6*2√2*2√3−8=
	3

	2
=		*4*6−8=16−8=8
	3

zef: Głupie błędy przez liczenie w pamięci

zef: jc fajny skrót na obliczenie pola

jc: Co skłoniło autora do zapisania takiego zadania, skoro zadanie ogólniejsze jest dużo łatwiejsze do rozwiązania? Wynik powinien być symetryczny względem a, b, co pozwala nam wychwycić pewne błędy. Podstawienie konkretnych liczb jest już zabawką.

Mila: zef, przeczytaj 16:47 . Tam masz zadania ułożone wg stopnia trudności.

zef: Oki, dziękuję poćwiczę to jeszcze,przez następne dni(jeśli będę miał czas) spróbuję cofnąć się do pochodnych a dokładniej do badania monotoniczności, więc możliwe że również będę potrzebował pomocy

zef: Zadanie pochodzi z książki matematyka zadania maturalne i egzaminacyjne część II Jerzy Janicki Tadeusz Korczyc Jerzy Nowakowski Na wstępie napisanie jest: Zbiór zawiera zadania maturalne i egzaminacyjne z 1976r...

Mariusz: zef zaczyna się rok szkolny więc odpuść sobie na razie całkowanie i skup się na zadaniach maturalnych Jeśli całkowanie cię interesuje to mogłeś je ćwiczyć w wakacje ale wtedy się nie odzywałeś

Mila: zef Teraz będziesz w ostatniej LO? Mogę podać zadania z początku roku szkolnego.

Mariusz: Obecne pierwszaki już mają już czteroletnie licea i pięcioletnie technika czy jeszcze tego nie przywrócili Ciekawe też co z licencjatami ? Jeśli je zlikwidują to dobrze by było dokończyć studia

Metis: Zapowiada się nowa reforma SW , takie zmiany przyniosą więcej szkód niż pozytywnych rezultatów

Krzysiek58: I po co sie tym zamartwiasz ?

Krzysiek58: Skonczysz studia 5−letnie i uzyskasz tytul magistra po napisaniu i obronieniu pracy Slonczysz studia zaoczne 4 letnie + i uzyskas stopien inzyniera po zdaniu egzaminu przed komisja na ocene Jak bedziesz chcial magistra to dwuletnia magisterka (tak bylo

Mariusz: Przykładowo mamy licencjat czy wobec tego że robią studia magisterskie bez licencjatu dobrym pomysłem jest skończenie magisterki z kursem pedagogicznym (do samego licencjatu nie warto było robić tego kursu )

Mariusz: Trochę zeszliśmy z tematu chociaż myślę że do zadań z całkami powinien wrócić po maturze (oczywiście jeśli je lubi)

Mariusz: A co do tej reformy to mnie się ona podoba i nie wiem czemu wprowadzili te całe licencjaty

Mariusz: Trzyletni system to pierwsza klasa powtórzenie wiadomości z szkoły podstawowej bądź gimnazjum trzecia klasa to przygotowanie do egzaminu i zostaje nam druga klasa

Mariusz: Mila nie zaszkodzi mu jak podasz te zadania Mnie ostał się tylko zbiór Dróbki i Szymańskiego z lat 1996 2000

Krzysiek58: Qulka bardzo lubi ten zbior zadan

zef: Moze macie racje jesli chodzi o calki, w wakacje przez prace nie zawsze mialem czas. Mila jak mozesz to podeslij mi te zadania

Krzysiek58: Pewnie masz juz dosc zbiorow zadan ale ja zaproponuje CI stary zbiorek zadana Jakub Wojcik Zbior pytan i zadan egzaminacyjnych z matematyki Dlaczego ? Dlatego ze na poczatku powtrzasz teorie z zadanaimi i pozniej sa zadania egzaminacyjne . Wada tego zbioru . sa tylko odpowiedzi do zadan bo zadania sa przewidziane do samodzielnego rozwiazania .

Mariusz: Krysicki i Włodarski zastosowali ten sam pomysł jeśli chodzi o analizę matematyczną tzn najpierw przypominają potrzebną teorię później dają zadania a na koniec dają odpowiedzi w których jednak zdarzają się błędy Po maturze możesz się nim zainteresować

Mila: zef jaki masz obowiązujący podręcznik i zbiór zadań.

zef: Jutro się najprawdopodobniej wszystkiego dowiem, bo mam zmianę nauczycieli

Oliwia9: Bede tu zagladac tez skorzystam

Mila: Potęga o wykładniku rzeczywistym− powtórzenie wg Świda, Kurczab: 1) oblicz (bez kalkulatora) a) √147²*6²+147²*8² b) ³√216*12+216*8+216*7 c) √113²−112²+√89²−80² d) √666²+888² 2)Uporzadkuj rosnąco liczby: x=(0,125)⁻⁸, y=64^1,5, z=128, t=(0,5)⁻¹², u=⁴√16 3) oblicz x: x*(⁴√3+⁴√2)*(⁴√3−⁴√2)=√48−√32 4) rozwiąż równania: (2√3−x)*(√3+1)=7+√3 b) √2*x²+2√3*x=−√2 c)

	1
(3−√2)2*x=
	(3+√2)2*x

d)

	x2−(0,25)−1*x+8(2/3)
(√2−1)*x=
	(√2+1)*x

Oliwia9: a) √147²*6²+p[147²*8²= √147²(36+64= √147²*√100= 147*10= 1470

zef: b)18 c)√(113−112)(113+112)+√(89−80)(89+80)=16+3*13=55 d)√111²*6²+111²*8²=√111²(6²+8²)=1110

zef:

	1
x=		−8=88=224
	8

y=2⁶)^1.5=2⁹ z=2⁷

	1
t=		−12=212
	2

u=2 u,z,y,t,x

zef: x(√3−√2)=√48−√32

	√48−√32
x=
	(√3−√2)

x=(√48−√32)(√3+√2) x=(√48−√32)(√3+√2) x=(4√3−4√2)(√3+√2) x=4(√3−√2)(√3+√2) x=4

zef: 4 zrobię innym razem

Mila:

zef: (2√3 − x)(√3+1)=7+√3 6+2√3−x√3−x=7+√3 −x(√3+1)=1−√3 −x=^1−√3)2₂ x=^{−(1−√3)2}₂ B √2x²+2√3x+√2=0 Δ=12−8

	−2√3−2
x1=
	2√2

	−2√3+2
x2=
	2√2

C x=1 lub −1, mianownik rozny od zera D mianownik rozny od zera x=−1

Mila: a) (2√3−x)*(√3+1)=7+√3 /*(√3−1) (2√3−x)*(3−1)=7√3−7+3−√3 (2√3−x)*2=6√3−4 /:2 2√3−x=3√3−2 2−√3=x x=2−√3 ===== b) √2x²+2√3x+√2=0 /*√2 2x²+2√6x+2=0 /:2 x²+√6*x+1=0 Δ=6−4=2

	−√6−√2		−√6+√2
x=		lub x=
	2		2

Mila: c) x≠0

	1
(3−√2)2*x=		⇔
	(3+√2)2*x

(3−√2)²*(3+√2)²*x²=1⇔ [(3−√2)*(3+√2)]²*x²=1 (9−2)²*x²=1 7²*x²=1

	1
x2=
	49

	1		1
x=−		lub x=
	7		7

d) x=1

Mariusz: Jeśli chodzi o całkowanie funkcji wymiernych to nie przećwiczyliśmy jeszcze przypadku gdy mianownik zawiera pierwiastki wielokrotne (mogą być zespolone) np

	x7+2
∫		dx
	(x2+x+1)2

	4x2−8x
∫		dx
	(x−1)2(x2+1)2

	x2+x+1
∫		dx
	x5−2x4+x3

	(x2−1)2
∫		dx
	(1+x2)3

	1
∫		dx
	x4(x3+1)2

	1
∫		dx
	(x2+2x+10)3

	(x+2)
∫		dx
	(x2+2x+2)3

	x5−x4−26x2−24x−25
∫		dx
	(x2+4x+5)2(x2+4)2

	3x4+4
∫		dx
	x2(x2+1)3

	5−3x+6x2+5x3−x4
∫		dx
	x5−x4−2x3+2x2+x−1

	9
∫		dx
	5x2(3−2x2)3

W tych całkach przyda się wydzielenie części wymiernej które podałem w schemaciku

	1
albo wzór redukcyjny na całkę ∫		dx który chciałem abyś wyprowadził
	(1+x2)n

Wzór redukcyjny przydaje się gdybyś chciał użyć standardowego rozkładu na sumę ułamków prostych Straciłeś wolny czas w wakacje który mógłbyś poświęcić na całkowanie więc teraz powinieneś skupić się na zadaniach maturalnych lecz mimo to widziałem że nadal liczysz całki

Mariusz: Ze zbiorów zadań mam tylko Dróbkę Szymańskiego jednak nie widzę w nim jakichś ciekawych zadań

zef: Tak, czasami jeszcze policzę jakieś całki żeby chociaż podstaw nie zapomnieć. Przeliczę te całki jak znajdę więcej czasu, uwzględniać te pierwiastki zespolone w liczeniu ? Bo jeśli tak to nie wiem czy sobie poradze

Mariusz: Masz do wyboru albo schemacik z wydzieleniem części wymiernej całki

	L(x)		L1(x)		L2(x)
∫		dx=		+∫		dx
	M(x)		M1(x)		M2(x)

M₁(x)=GCD(M(x),M'(x)) M(x)=M₁(x)M₂(x) deg L₁(x) < deg M₁(x) deg L₂(x) < deg M₂(x) Liczniki L₁(x) oraz L₂(x) znajdujesz metodą współczynników nieoznaczonych albo standardowy rozkład na sumę ułamków prostych Jeśli chcesz użyć standardowego rozkładu na sumę ułamków prostych

	1
to przyda ci się wzór redukcyjny na całkę ∫		dx
	(1+x2)n

Mariusz: http://mariuszm2011.republika.pl/rational.gif http://mariuszm2011.republika.pl/0103.gif

zef: Odświeżam żeby nie przepadło.

	x7+2		x7+2
∫		dx=∫		dx
	(x2+x+1)2		x4+3x3+3x2+2x+1

	4x3−6x2−5x
(x7+2):(x4+3x3+3x2+2x+1)=x3−2x2+x+2+
	(x4+3x3+3x2+2x+1)

	x7+2		4x3−6x2−5x
∫		dx=∫x3−2x2+x+2dx + ∫
	x4+3x3+3x2+2x+1		(x4+3x3+3x2+2x+1)

	x4		2x3		x2		4x3−6x2−5x
∫x3−2x2+x+2dx=		−		+		+2x ∫
	4		3		2		(x4+3x3+3x2+2x+1)

	4x3−6x2−5x
∫		=?
	(x4+3x3+3x2+2x+1)

x(4x2−6x−5)
	Co w tym przypadku robić dalej ? Rozkład na ułamki proste
(x4+3x3+3x2+2x+1)

słabo by wyglądał przez te nieciekawe pierwiastki

Adamm:

4x3−6x2−5x		Ax+B		Cx+D
	=		+
(x2+x+1)2		x2+x+1		(x2+x+1)2

zef: odwołania do poprzednich tematów: (żeby nie zgubić) https://matematykaszkolna.pl/forum/328959.html https://matematykaszkolna.pl/forum/323858.html

4x3−6x2−5x		Ax+B		Cx+D
	=		+
(x2+x+1)2		x2+x+1		(x2+x+1)2

4x³−6x²−5x=(Ax+B)(x²+x+1)+Cx+D 4x³−6x²−5x=Ax³+Ax²+Ax+Bx²+Bx+B+Cx+D 4x³−6x²−5x=x³(A)+x²(A+B)+x(A+B+C)+D+B A=4 A+B=−6→B=−10 4−10+C=−5 C=1 D=10

	4x−10		−5x+10
∫		dx+∫		dx
	x2+x+1		(x2+x+1)2

	4x−10		2x−5
∫		dx=2∫		dx
	x2+x+1		x2+x+1

	1
I tutaj nie wiem jakie dać podstawienie myślałem nad tym że (x+		)=√3/4t ale trudno by
	2

się dalej liczyło

Adamm:

	f'(x)
do pierwszego, rozdziel na		oraz na stałą/wielomian, stałą/wielomian policz
	f(x)

podstawieniem pod całkę z arcusa tangesa

Adamm:

	f'(x)
drugą całkę rozbij na		oraz na stałą/wielomian, stałą przez wielomian
	(f(x))2

policz ze wzoru rekurencyjnego, lub po prostu przez części

zef:

	2x−5
2∫		dx=
	x2+x+1

	2x+1−6
2∫		dx=
	x2+x+1

	2x+1		6
2∫		dx−∫		dx=
	x2+x+1		x2+x+1

	1
2ln(x2+x+1)−6∫		dx=
	x2+x+1

	1
2ln(x2+x+1)−6∫		dx=
	1   3   (x+ )+ 2   2   4

	1   x+   2
2ln(x2+x+1)−8arctan(		)+C
	3/4

===================================== podsumowując wynik:

x4		2x3		x2		1   x+   2
	−		+		+2x+2ln(x2+x+1)−8arctan(		)+
4		3		2		3/4

	−5x+10
∫		dx
	(x2+x+1)2

	−5x+10
i właśnie została mi ta całka do obliczenia: ∫		dx
	(x2+x+1)2

zef: ∫U{−5x+10}{(x²+x+1)²dx=

	5		2   18   2x− −   5   5
−		∫		dx=
	2		(x2+x+1)2

	5		9
−		[ln(x2+x+1)2]+∫		dx
	2		(x2+x+1)2

	5		1
−		[ln(x2+x+1)2]+9∫		dx
	2		((x+1/2)+(3/4)2)2

	5		x+1
−		[ln(x2+x+1)2]+9arctan(		)2
	2		3/4

Czyli odp to :

x4		2x3		x2
	−		+		+2x+2ln(x2+x+1)
4		3		2

	x+1/2		5		x+1
−8arctan(		−		[ln(x2+x+1)2]+9arctan(		)2
	3/4		2		3/4

Może ktoś wskazać błędy i sprawdzić?

Mariusz:

	dx
Spróbuj jednak wyprowadzić ten wzór redukcyjny na ∫
	(1+x2)n

Zapisz licznik w postaci 1=(1+x²)−x² Rozbij na sumę całek W pierwszej skróć licznik z mianownikiem Drugą policz przez części przyjmując u=x

	x
dv=−		dx
	(1+x2)n

Ten wzór redukcyjny przyda ci się jeśli nie chcesz używać schematu który podałem 24 wrz 16:45

Mariusz:

	x
Jeśli od razu nie widzisz pierwotnej −
	(1+x2)n

to sobie pomocniczo podstaw za trójmian kwadratowy w mianowniku

Mariusz:

	−5x+10		5	2x−4
∫		dx=−			dx
	(x2+x+1)2		2	(x2+x+1)2

	5		2x+1		25		dx
=−		∫		dx+		∫
	2		(x2+x+1)		2		(x2+x+1)2

Aby policzyć pierwszą całkę podstawiasz za trójmian kwadratowy w mianowniku Aby policzyć drugą całkę sprowadzasz trójmian do postaci kanonicznej

	1		√3
podstawiasz pomocniczo (x+		)=		t
	2		2

a następnie korzystasz ze wzoru redukcyjnego którego zaproponowałem abyś wyprowadził Inny sposób to wydzielenie części wymiernej Niech mianownik zawiera pierwiastki wielokrotne

	R(x)		R1(x)		R2(x)
∫		dx=		+∫		dx
	M(x)		M1(x)		M2(x)

Wielomian M₂(x) ma takie same pierwiastki co M(x) tyle że pojedyncze Krotność pierwiastków wielomianu M₁(x) jest o jeden mniejsza niż wielomianu M(x) Liczniki R₁(x) oraz R₂(x) znajdujesz metodą współczynników nieoznaczonych (za współczynniki wielomianów R₁(x) oraz R₂(x) przyjmujesz współczynniki literowe i różniczkujesz powyższą równość aby je obliczyć) Gdybyś znał podstawy algebry to wielomiany w mianownikach tzn M₁(x) oraz M₂(x) można by znaleźć bez rozkładania wielomianu M(x) W twoim przykładzie

	−5x+10		a1x+a0		b1x+b0
∫		dx=		+∫		dx
	(x2+x+1)2		(x2+x+1)2−1		x2+x+1

	−5x+10		a1x+a0		b1x+b0
∫		dx=		+∫		dx
	(x2+x+1)2		x2+x+1		x2+x+1

Różniczkujesz obustronnie powyższą równość aby obliczyć współczynniki

−5x+10		a1(x2+x+1)−(a1x+a0)(2x+1)
	=
(x2+x+1)2		(x2+x+1)2

	b1x+b0
+
	x2+x+1

−5x+10		a1x2+a1x+a1−2a1x2−a1x−2a0x−a0
	=
(x2+x+1)2		(x2+x+1)2

	(b1x+b0)(x2+x+1)
+
	(x2+x+1)2

−5x+10=b₁x³+b₁x²+b₁x+b₀x²+b₀x+b₀−a₁x²−2a₀x+a₁−a₀ −5x+10=b₁x³+(b₁+b₀−a₁)x²+(b₁+b₀−2a₀)x+b₀+a₁−a₀ b₁=0 b₁+b₀−a₁=0 b₁+b₀−2a₀=−5 b₀+a₁−a₀=10 b₁=0 b₀=a₁ a₁−2a₀=−5 2a₁−a₀=10 b₁=0 b₀=a₁ a₁=−5+2a₀ 3a₀=20 b₁=0 b₀=a₁ 3a₁=25 3a₀=20

	−5x+10		1	25x+20		1		25
∫		dx=			+		∫		dx
	(x2+x+1)2		3	x2+x+1		3		x2+x+1

Mariusz:

	5−3x+6x2+5x3−x4
∫		dx
	x5−x4−2x3+2x2+x−1

Stosujemy schemacik

	R(x)		R1(x)		R2(x)
∫		dx=		+∫		dx
	M(x)		M1(x)		M2(x)

Czynniki występujące w rozkładzie wielomianu M(x) występują także w rozkładzie pochodnej wielomianu M(x) tyle że z krotnością mniejszą o jeden (Oprócz tego w rozkładzie pochodnej wielomianu mogą występować inne czynniki , pochodna wielomianu ma stopień o jeden mniejszy niż różniczkowany wielomian, więc aby policzyć mianownik części wymiernej bierzesz NWD mianownika funkcji podcałkowej M(x) oraz jej pochodnej ) Aby policzyć NWD wielomianów wcale nie musisz ich rozkładać (oczywiście jeśli masz dany rozkład na czynniki to możesz z niego skorzystać) Bierzesz reszty z kolejnych dzieleń

	5−3x+6x2+5x3−x4
∫		dx
	x5−x4−2x3+2x2+x−1

M(x)=x⁵−x⁴−2x³+2x²+x−1 M'(x)=5x⁴−4x³−6x²+4x+1

1		1
	x−
5		25

x⁵−x⁴−2x³+2x²+x−1:5x⁴−4x³−6x²+4x+1

	4		6		4		1
−x5+		x4+		x3−		x2−		x
	5		5		5		5

	1		4		6		4
−		x4−		x3+		x2+		x−1
	5		5		5		5

	1		4		6		4		1
		x4−		x3−		x2+		x+
	5		25		25		25		25

	24		24		24		24
−		x3+		x2+		x−
	25		25		25		25

W wyniku dzielenia otrzymujesz

	1		1
iloraz		x−
	5		25

	24		24		24		24
reszta −		x3+		x2+		x−
	25		25		25		25

Iloraz ignorujesz a do dalszych obliczeń bierzesz resztę (stałą możesz wyciągnąć) Kolejne dzielenie 5x+1 5x⁴−4x³−6x²+4x+1:x³−x²−x+1 −5x⁴+5x³+5x²−5x x³−x²−x+1 −x³+x²+x−1 0 W wyniku dzielenia otrzymujesz iloraz 5x+1 reszta 0 więc x³−x²−x+1 jest największym wspólnym dzielnikiem wielomianów x⁵−x⁴−2x³+2x²+x−1 oraz 5x⁴−4x³−6x²+4x+1 a zatem jest także mianownikiem części wymiernej całki Aby znaleźć mianownik funkcji która zostanie pod całką dzielisz wielomian x⁵−x⁴−2x³+2x²+x−1 przez wielomian x³−x²−x+1 x²−1 x⁵−x⁴−2x³+2x²+x−1:x³−x²−x+1 −x⁵+x⁴+x³−x² −x³+x²+x−1 x³−x²−x+1 0 W wyniku dzielenia otrzymujesz iloraz x²−1 reszta 0 Tym razem interesuje cię iloraz więc mianownik części wymiernej to x³−x²−x+1 mianownik funkcji wymiernej która zostaje pod całką to x²−1 Za współczynniki wielomianów w liczniku bierzesz współczynniki literowe pamiętając że stopnie tych wielomianów są mniejsze od stopni wielomianów w mianowniku W tym przykładzie będziesz miał

	5−3x+6x2+5x3−x4
∫		dx=
	x5−x4−2x3+2x2+x−1

a2x2+a1x+a0		b1x+b0
	+∫		dx
x3−x2−x+1		x2−1

Współczynniki liczników obliczasz różniczkując powyższą równość Będziesz musiał także sprowadzić ułamki do wspólnego mianownika, porównać wielomiany w licznikach i rozwiązać układ równań

Mariusz: Jeśli chodzi o całkę

	x7+2
∫		dx
	(x2+x+1)2

to po podzieleniu licznika przez mianownik została ci całka z wielomianu oraz całka

	4x3−6x2−5x
∫		dx
	(x2+x+1)2

i tej funkcji podcałkowej nie musisz rozkładać na sumę ułamków prostych chyba że chcesz skorzystać z wzoru redukcyjnego Zamiast wzoru redukcyjnego możesz wydzielić część wymierną całki We wpisie z 30 sie 22:14 przedstawiłem schemacik całkowania funkcji wymiernych z wydzieleniem części wymiernej całki oraz podstawienia prowadzące do całek z funkcji wymiernych We wpisie z 29 wrz 10:51 przedstawiłem schemacik całkowania funkcji wymiernych z użyciem wzoru redukcyjnego i rozpisałem podstawienia sprowadzające całki postaci ∫R(x,√ax²+bx+c)dx do całek z funkcji wymiernych Zdaje mi się że ich nie przejrzałeś