całki zef: Mógłby mi ktoś sprawdzić tą całkę ? Dawno nic nie rozwiązywałem i chcę wiedzieć czy w tych prostszych nie popełniam błędów

	21x+13
∫		dx
	x2−6x+25

mianownik: (x−3)²+16

	21x+13
∫		dx
	(x−3)2+16

x−3=√16t x−3=4t d/dx

	4dt
1=
	dx

dx=4dt podstawiam:

	4t*21+76
∫		(4dt)
	16t2+16

	4t*21+76
∫		(dt)
	4t2+4

1		4t*21+76
	∫		(dt)
4		t2+1

Rozbijam na 2 całki

	t		1		76
21∫		dt +		∫		dt
	t2+1		4		t2+1

	2t		1
10,5∫		dt+19∫		dt
	t2+1		t2+1

10,5In|t²+1|+19arctan(t)

	x−3		x−3
10,5In|(		)2+1|+19arctan|		|
	4		4

	x2−6x+25		x−3
10,5In|(		|+19arctan|		|
	16		4

Mila:

	21x+13
∫		dx=..
	(x−3)2+16

[x−3=4t, dx=4dt, x=4t+3]

	21*(4t+3)+13
..=4∫		dt=
	16t2+16

	1		84t+76
=		∫		dt=
	4		t2+1

..

	21		x−3
=		ln|x2−6x+25|+19arctg|		|+C
	2		4

Dobrze masz.

zef: Dziękuję, wracam do czytania na temat całek w których stosuje się rozkład na ułamki proste

Mila: Powodzenia.

Mariusz: Jest to kontynuacja tematu z wątku https://matematykaszkolna.pl/forum/323858.html

Mariusz: Chciałeś zacząć od rozkładu wielomianów trzeciego i czwartego stopnia na czynniki Czytałeś już coś o liczbach zespolonych ?

zef: Tak chciałem zacząć od tych wielomianów, co do liczb zespolonych to znam podstawy podstaw

Mariusz: Liczby zespolone nie są konieczne do rozłożenia tych wielomianów ale ich znajomość pomaga Liczbę zespoloną można przedstawić jako element produktu kartezjańskiego dwóch zbiorów rzeczywistych Geometrycznie jest to punkt na płaszczyźnie Mamy dwie postacie liczby zespolonej : postać algebraiczna z=a+bi (związana z prostokątnym , kartezjańskim układem współrzędnych) Jeżeli utożsamimy liczbę zespoloną z punktem na płaszczyźnie to część rzeczywista jest reprezentowana przez współrzędna odciętych a część urojona przez współrzędną rzędnych postać trygonometryczna z=r(cos(θ)+i sin(θ)) (związana z biegunowym układem współrzędnych) Moduł liczby zespolonej to długość promienia wodzącego układu biegunowego a argument liczby zespolonej to miara kąta między osią biegunową a promieniem wodzącym Zbiór liczb zespolonych nie jest liniowo uporządkowany zatem porównywanie liczb zespolonych jest ograniczone tylko do relacji równe Liczby zespolone są równe gdy ich części rzeczywiste są równe oraz części urojone są równe Nierówności znanych z liczb rzeczywistych tutaj nie ma Zbiór liczb zespolonych jest wprawdzie częściowo uporządkowany ale tym nie będziemy się zajmować Jednostka urojona Jednostka urojona ma tę własność że jeśli podniesiemy ją do kwadratu dostaniemy minus jedynkę Sprzężeniem zespolonym nazywamy liczbę której część rzeczywista i moduł pozostają bez zmian a część urojona i argument zmieniają znak właściwości sprzężenia z+z*=2Re(z) zz*=|z|² Dodawanie liczb zespolonych Dodajemy część rzeczywistą jednej liczby do części rzeczywistej drugiej liczby Dodawanie liczb zespolonych przypomina dodawanie wektorów (a+bi)+(c+di)=(a+c)+(b+d)i Odejmowanie liczb zespolonych Od części rzeczywistej odjemnej odejmujemy część rzeczywistą odjemnika a od części urojonej odjemnej odejmujemy część urojoną odjemnika (a+bi)−(c+di)=(a−c)+(b−d)i Mnożenie liczb zespolonych Liczby zespolone mnożysz tak samo jak mnożysz dwumiany na liczbach rzeczywistych z zachowaniem własności liczby urojonej i²=−1 Liczby zespolone możesz mnożyć także na postaci trygonometrycznej Mnożysz moduły a argumenty dodajesz (a+bi)(c+di)=(ac−bd)+(bc+ad)i z₁z₂=r₁r₂(cos(θ₁+θ₂)+i sin(θ₁+θ₂)) Dodawanie i mnożenie zachowują swoje własności które miały na liczbach rzeczywistych tj przemienność , łączność a w przypadku mnożenia także rozdzielność względem dodawania Dzielenie liczb zespolonych Korzystamy tutaj z własności sprzężenia zz*=|z|² oraz z tego że moduł jest liczbą rzeczywistą i sprowadzamy dzielenie do mnożenia rozszerzając licznik i mianownik przez sprzężenie mianownika Dzielenie liczb zespolonych można wykonać także na postaci trygonometrycznej Dzielisz moduł dzielnej przez moduł dzielnika a od argumentu dzielnej odejmujesz argument dzielnika

a+bi		(a+bi)(c−di)		(ac+bd)+(bc−ad)i
	=		=
c+di		(c+di)(c−di)		c2+d2

z1		r1
	=		(cos(θ1−θ2)+i sin(θ1−θ2))
z2		r2

Potęgowanie liczb zespolonych Tutaj mamy wzór de Moivre Załóżmy że liczba zespolona zapisana jest w postaci z=r(cos(θ)+i sin(θ)) zⁿ=rⁿ(cos(nθ)+i sin(nθ)) Pierwiastek liczby zespolonej Tutaj także korzystamy z wzoru de Moivre jednak trzeba pamiętać że wartością pierwiastka nie jest liczba zespolona a zbiór rozwiązań równania xⁿ=z

	θ+2kπ		θ+2kπ
z1/n=r1/n(cos(		)+i sin(		))
	n		n

k=0,1,2,..,n−1 Tutaj warto zwrócić uwagę na szczególny przypadek pierwiastka tzn pierwiastek z jedynki

zef: Przeczytałem to co napisałeś, najtrudniej będzie mi chyba zrozumieć te wszystkie trygonometryczne zapisy. Mając wzór:

a+bi		(a+bi)(c−di)		(ac+bd)+(bc−ad)i
	=		=
c+di		(c+di)(c−di)		c2+d2

To w ostatnim mianownik plus wziął się z tego że początkowo był tam wzór skróconego mnożenia "a²−b²" ale przez to że powstanie i² zmieniamy znak. Dobrze rozumiem ?

zombi: Tak, dokładnie stąd bierze się plus. Ogólnie a²+b² = (a+bi)(a−bi)

Mariusz: zef ćwiczyłeś przechodzenie między kartezjańskim a biegunowym układem współrzędnych ?

zef: Niestety właśnie nawet nie wiem co to jest

Mariusz: Oś biegunowa jest to półprosta o początku w początku układu czyli w tzw biegunie Promień wodzący jest to odcinek o końcach w danym punkcie oraz w biegunie Promień wodzący tworzy z osią biegunową kąt którego miara bywa nazywana amplitudą Jeśli dany punkt P zrzutujemy na oś biegunową to otrzymamy trójkąt OP'P Długość promienia wodzącego obliczymy stosując w trójkącie OP'P twierdzenie Pitagorasa Miarę kąta obliczymy na podstawie funkcji trygonometrycznych z trójkąta OP'P

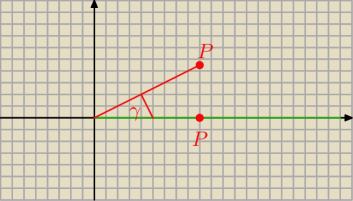
zef: Nie wiem czy dobrze rozumiem Zielone− oś biegunowa Czerwone− promień wodzący γ−Amplituda

Mariusz: Mniej więcej to jest to (rzut punktu P mogłeś jakoś inaczej oznaczyć) Jeśli chodzi o miarę kąta to tak właściwie obliczasz ją korzystając z funkcji odwrotnej do wybranej funkcji trygonometrycznej np tangens a na podstawie wartości funkcji trygonometrycznych takich jak sinus i cosinus ustalasz odpowiednią ćwiartkę Miałeś coś o funkcjach w tym o funkcji odwrotnej ?

Mariusz: zef miara tego kąta między osią biegunową prawdopodobnie i promineniem wodzącym się jakoś inaczej nazywa więc z wikipedii nie warto korzystać Na lekcji nie nazywaliśmy go inaczej jak argument liczby zespolonej albo opisowo Amplituda bardziej pasuje do modułu a faza do argumentu ale nie jestem pewny czy to poprawne określenia Już ponad 16 lat minęło jak skończyłem szkołę i chciałem sobie trochę nazewnictwo przypomnieć a tutaj wydaje mi się że wikipedia kłamie więc zachowaj do niej dystans

zef: Teoria teorią ale może przejdziemy już do jakiś zadań dot. wielomianów, zespolonych lub całek.

Jerzy:

	ex − e−x
∫		dx
	ex + e−x

zef: Pamiętam że już kiedyś dostałem od ciebie ten przykład

ex−e−x		ex−1/ex		ex
	=		=		=
ex+e−x		ex+e−x		ex+e−x−ex

ex		ex
	=		=e2x
e−x		1/ex

	1
∫e2xdx=		e2x
	2

Tyle wymyśliłem, nie wiem czy coś z tego dobrze.

Jerzy: Specjalnie dałem ci tą całkę, abyś zauważył motyw,który często wkorzystujemy przy obliczaniu całek ( warto ten wzór zapamiętać )

	f'(x)
∫		dx = lnIf(x)I + C
	f(x)

i policz jeszcze raz ta całkę

Jerzy: I do praktyki ( wykorzystaj ten motyw):

	x − 3
∫		dx
	x2 + 1

Jerzy: I jeszcze jeden "myk":

	f'(x)
∫		dx = √f(x) + C
	2√f(x)

	x
przykład: ∫		dx = ... ?
	√x2 − 4

zef: Z tym e^x to nie wiem czy moje przekształcenia są dobre i potrzebne

	x−3
∫		dx
	x2+1

x²+1 /d/dx =2x

	(2x)*1/2−3
∫		dx
	x2+1

1		(2x)		1
	∫		dx −3∫		dx
2		x2+1		x2+1

1
	In|x2+1|−3arctan|x|+C
2

Jerzy: Perfect ... a pierwsza całka, to po prostu: ln Ie^x + e^−xI + C

zef:

	x
∫		dx
	√x2−4

[x²−4=t d/dx 2x=dt/dx 2xdx=dt xdx=dt/2]

1		1		1		1	t1/2
	∫		dt=		∫t−1/2dt=			+C=√t+C=√x2−4+C
2		√t		2		2	1/2

Chyba wybrałem najdłuższą drogę liczenia tego, ale udowodniłem co trzeba było

Benny: Dlaczego moduł w arcusie?

zef: Właśnie nie wiem czy w arcusie i w In należy stosować nawias czy moduł ?

Jerzy: A jak sobie radzisz z pochodnymi ? Na innym forum , student ( jak myślę ) wstawił taką funkcję: f(x) = x^2ln(x2+1)

Jerzy: Moduł tylko w logarytmie ( nie zauważyłem)

Jerzy:

	x		2x
∫		dx = ∫		dx = .... ze wzoru .... = √x2 − 4 + C
	√x2 − 4		2√x2 − 4

zef: Z pochodnymi sobie radziłem w miarę dobrze, dużo rzeczy pozapominałem i co jakiś czas zaglądam do wzorków.

Jerzy: To polic pochodną z f(x) = (sinx)^cosx

zef: Łatwo powiedzieć "policz" nie mam nawet pomysłu od czego tutaj zacząć , przecież jest zmienna do potęgi w której też jest zmienna

zef: Co do pochodnych to liczyłem tylko takie które są na poziomie licealnym

Jerzy: Sorry... f(x) = (sinx)^cosx = e^ln(sinx)cosx = e^{cosx*ln(sinx)} ... i próbuj teraz

Jerzy: OK .... ale spróbuj

Jerzy: Zapamiętaj ten wzór: [(f(x))^g(x)]' = (f(x))^g(x)*[g(x)*ln(f(x)]'

zef: [e^{cosx*In(sinx)}]'=e^cosxIn(sinx)*[cosx*In(sinx)]'

	1		cosx
[cosx*In(sinx)]'=−sinx*(In(sinx))+cosx*		=−sinx*(In(sinx))+
	sinx		sinx

czyli mam:

	cosx
ecosxIn(sinx)*[−sinx*(In(sinx))+		]
	sinx

Tyle potrafię

Jerzy: Prawie perfect przeanalizuj pochodną z: ln(sinx)

zef:

	1		cosx
[In(sinx)]'		*cosx=		Czy to pochodna złożona ?
	sinx		sinx

Jerzy: Dokładnie tak , czyli .... = ctgx

Jerzy: A teraz: ∫ctgxdx = ...?

zef:

	cosx
∫ctgxdx=∫		dx
	sinx

[t=sinx d/dx dt/dx=cosx cosxdx=dt]

	dt
∫		= In|t|+C= In|sinx| + C To akurat było proste
	t

Jerzy: Popatrz 16:47 .... to jest właśnie ten wzór.

zef: Aj faktycznie, ale nic się nie stało jak rozpisałem

Jerzy: Pewnie ,że nic ( nie wszystkie wzory się pamięta ) rozpisujesz krótko: t = sinx , dt = cosxdx

zef: Ok, będę pamiętał

Jerzy: Przymierz się do pochodnej z 17:15

zef: Jakaś wskazówka ?

Jerzy: 17:31

zef: [x^2ln(x2+1)]'=x^2ln(x2+1)*[2In(x²+1)*In(x)]'=

	2		1
x2ln(x2+1)*[		*2x*In(x)+2In(x2+1)*		]=
	x2+1		x

	4xIn(x)		2In(x2+1)
x2ln(x2+1)*[		+		]
	x2+1		x

Jerzy:

Jerzy: Możesz pokazać studentowi , jak się liczy tą pochodną

zef:

Jerzy: Jest powód do radości, bo chyba jesteś przed maturą ?

zef: Tak, we wrześniu idę do klasy maturalnej, trzeba się będzie wziąć do nauki

Jerzy: Masz tzw. smykałkę do matematyki

Jerzy: I teraz pora na równania różniczkowe

zef: Brzmi strasznie Już pora na takie równania, nie powinienem czegoś jeszcze przećwiczyć ?

Jerzy: Całki i pochodne

Mariusz: Ładnie pora na równania różniczkowe gdy jeszcze całkować dobrze nie umie i nie chce poćwiczyć algebry liniowej która też mu się przyda I ty się chwaliłeś że byłeś nauczycielem

Mariusz: Algebra liniowa przydaje się do całkowania funkcji wymiernych a później do układów równań rekurencyjnych i różniczkowych więc nie bez powodu chcę aby ją przećwiczył Zanim przejdziemy do całek z podstawieniami chcę aby przećwiczył całki z funkcji wymiernych ponieważ te opierają się głównie na liniowości całki i algebrze liniowej do tego dochodzą dwa łatwe podstawienia Gdy wydzielimy część wymierną całki to całkowanie przez części nie będzie potrzebne Podstawienia często sprowadzają całki do całek z funkcji wymiernych Z tego co pamiętam to został nam do rozpatrzenia jeszcze jeden przypadek no i z racji tego że jest w średniej to przydałoby się jeszcze powtórzyć to co powinien już umieć

zef: Jaki przypadek odnośnie całek został ?

Mariusz: Co do nazewnictwa w układzie biegunowym to w tablicach Mizerskiego są dwa określenia na miarę tego kąta tj amplituda i faza (trochę dziwne ale cóż) Rozkładanie wielomianów chcesz ? Masz równanie wielomianowe a₃x³+a₂x²+a₁x+a₀=0

	a2
Stosujesz podstawienie x=y−
	3a3

i dzielisz równanie przez współczynnik przy x³ Otrzymujesz równanie y³+py+q=0 Stosujesz drugie podstawienie y=u+v (u+v)³+p(u+v)+q=0 u³+3u²v+3uv²+v³+p(u+v)+q=0

	p
u3+v3+q+3(u+v)(uv+		)=0
	3

u³+v³+q=0

	p
uv+		=0
	3

u³+v³=−q

	p
uv=−
	3

u³+v³=−q

	p3
u3v3=−
	27

Powyższy układ równań to wzory Vieta dla równania kwadratowego o pierwiastkach u³ oraz v³

	p3
t2+qt−		=0
	27

	p3   −q−√q2+4   27
u3=
	2

	p3   −q+√q2+4   27
v3=
	2

	q		p		p
u3=−		−√(		)2+(		)3
	2		2		3

	q		p		p
v3=−		+√(		)2+(		)3
	2		2		3

Wyciągasz pierwiastek trzeciego stopnia z u³ oraz v³ korzystając ze wzoru de Moivre tak aby spełniony był układ równań u³+v³=−q

	p
uv=−
	3

Gdy już będziesz miał takie u oraz v spełniające układ u³+v³=−q

	p
uv=−
	3

to kolejne znajdziesz korzystając z pierwiastków trzeciego stopnia z jedynki Jeśli chodzi o równanie czwartego stopnia to pomysł z zapisaniem wielomianu czwartego stopnia w postaci iloczynu dwóch trójmianów kwadratowych jest dobrym pomysłem jednak może być żmudne rachunkowo

	a3
Możesz wprawdzie na początku zastosować znane podstawienie x=y−
	4a4

a następnie równanie dwukwadratowe rozpatrzeć oddzielnie ale czasami zdarzy się że nie skrócisz rachunków tak bardzo Mamy równanie a₄x⁴+a₃x³+a₂x²+a₁x+a₀=0

	a3
Stosujemy podstawienie y=x−
	4a4

a następnie dzielimy równanie przez współczynnik przy x⁴ Otrzymujemy równanie y⁴+b₂y²+b₁y+b₀=0 Rozpatrujemy dwa przypadki 1. b₁=0 Mamy wtedy tzw równanie dwukwadratowe (y²)²+b₂(y²)+b₀=0 2. b₁≠0 Stosujemy rozkład (y²−py+q)(y²+py+r)=y⁴+b₂y²+b₁y+b₀ Po wymnożeniu i porównaniu współczynników dostajemy układ równań którego rozwiązanie wymaga rozwiązania równania wielomianowego trzeciego stopnia na p² Wyodrębniłem równanie dwukwadratowe aby uniknąć możliwości dzielenia przez zero Sprowadzenie wielomianu czwartego stopnia najpierw do postaci różnicy kwadratów a później do iloczynu dwóch trójmianów na ogół wymaga mniej obliczeń a₄x⁴+a₃x³+a₂x²+a₁x+a₀=0

	a3		a2		a1		a0
x4+		x3+		x2+		x+		=0
	a4		a4		a4		a4

	a3		a2		a1		a0
x4+2		x3=−		x2−		x−
	a4		a4		a4		a4

	a3		a32
x4+2		x3+		x2
	2a4		4a42

	a32		a2		a1		a0
=(		−		)x2−		x−
	4a42		a4		a4		a4

	a3
(x2+		x)2
	2a4

	a32		a2		a1		a0
=(		−		)x2−		x−
	4a42		a4		a4		a4

Jak widzisz lewą stronę równania sprowadziliśmy do kwadratu korzystając ze wzoru skróconego mnożenia Prawa strona równania jest trójmianem kwadratowym więc będzie kwadratem gdy jego wyróżnik będzie równy zero Gdybyśmy liczyli wyróżnik od razu mogłoby się okazać że wyróżnik nie jest zerowy więc trzeba go uzależnić od jakiejś zmiennej Zmienną wprowadzamy tak aby lewa strona nadal była kwadratem czyli znowu korzystamy z wzorów skróconego mnożenia

	a3		y
(x2+		x+		)2
	2a4		2

	a32		a2		a3		a1
=(y+		−		)x2+(		y−		)x
	4a42		a4		2a4		a4

	y2		a0
+		−		=0
	4		a4

Δ=0

	y2		a0		a32		a2
4(		−		)(y+		−		)−
	4		a4		4a42		a4

	a3		a1
(		y−		)2=0
	2a4		a4

	4a0		a32		a2
(y2−		)(y+		−		)−
	a4		4a42		a4

	a3		a1
(		y−		)2=0
	2a4		a4

...

Mariusz: Jeśli chodzi o całkowanie funkcji wymiernych to został przypadek gdy mianownik ma pierwiastki wielokrotne ale abyś mógł przećwiczyć sposobem którym chce ci pokazać musisz umieć liczyć także NWD wielomianów NWD wielomianów przydaje się także w rozkładaniu wielomianów Jeżeli chodzi o NWD wielomianów to liczy się go podobnie jak na liczbach 1. Korzystając z rozkładu na czynniki 2. Biorąc kolejne reszty z dzielenia Pierwszy sposób jest dobry tylko wtedy gdy rozkład na czynniki mamy dany

zef: wygląda na bardzo skomplikowane Bardziej mnie to przeraża niż te całki które robiłem Zacznijmy może od wielomianu 3 stopnia i szukania jego pierwiastków. Możesz mi dać jakiś przykład, spróbowałbym to zrobić na podstawie tego co napisałeś

Mila: zef a planimetrię już opanowałeś? W klasie maturalnej masz : 1) funkcja wykładnicza i logarytmiczna (wykresy, przekształcenia wykresów, własności funkcji, równania, nierówności, zastosowania w zadaniach z kontekstem realistycznym) 2) Analiza matematyczna granice ciągów (powtórzenie) Granica funkcji w punkcie (w tym z definicji) Ciągłość funkcji w punkcie ciągłość funkcji w zbiorze asymptoty Pochodna funkcji w punkcie ( z definicji) Styczna do wykresu funkcji Badanie przebiegu funkcji zadania optymalizacyjne. 3) Geometria analityczna 4) kombinatoryka i rach. prawdopodobieństwa 5) elementy statystyki opisowej 5) Geometria przestrzenna (powtórzenie planimetrii)

Mariusz: Co do NWD wielomianów to nie jest to skomplikowane jeśli sprawnie wykonujesz dzielenie wielomianów z resztą Jeśli chodzi o przykład wielomianu trzeciego stopnia do rozłożenia to x³−x²−2x+8 Tutaj pierwiastek znajdziesz w dzielnikach wyrazu wolnego a mając pierwiastek łatwo rozłożysz wielomian ale spróbuj go rozłożyć sposobem który podałem

zef: Jeśli chodzi o planimetrię to nic więcej nie ćwiczyłem, póki co sam nie wiem za co się zabrać :<

Mariusz: Oczywiście tematy od użytkownika Mila też powinieneś sobie przećwiczyć uprzednio czytając trochę teorii na ten temat Ale skoro chcesz całkować to podstawy algebry ci nie zaszkodzą

Mila: zef Na maturze masz sporo geometrii, zatem na razie zacznij powtarzać planimetrię, zależy co już miałeś wcześniej, bo różnie jest realizowany materiał. W geometrii przestrzennej dojdą nowe problemy i nie rozwiążesz zadania bez znajomości planimetrii, a jest tam sporo różnych zadań. Jaki masz zbiór zadań?

Mariusz: Przykładowo do całek postaci ∫R(x,√ax²+bx+x)dx stosujesz podstawienia I √ax²+bx+c=t−√ax a>0 II √ax²+bx+c=xt+√c c>0 III √ax²+bx+c=(x−x₀)t b²−4ac>0 przy czym pierwsze i trzecie wystarczą do sprowadzenia tych całek do całek z funkcji wymiernej Po tych podstawieniach możesz dostać także całkę z funkcji w której mianownik będzie miał pierwiastki wielokrotne To jest jeden z przykładów , podstawień sprowadzających całki do całek z funkcji wymiernych jest więcej więc dlatego chciałem abyś je dobrze przećwiczył

Jerzy: Cześć [FMila.... Ty usunęłaś mój wpis ?

zef: x³−x²−2x+8

	1
x=y+
	3

	1		1		1
(y+		)3−(y+		)2−2(y+		)+8
	3		3		3

	1		1		2		3		2
y3+y2+		y+		−(y2+		y+		)−2y−		+8
	3		27		3		27		3

	1		1		2		3		18
y3+y2+		y+		−y2−		y−		−2y−		+8
	3		27		3		27		27

	7		20		216
y3−		y−		+
	3		27		27

	7		196
y3−		y+
	3		27

y=u+v

	7		196
(u+v)3−		(u+v)+		=0
	3		27

	7		196
u3+3u2v+3uv2+v3−		(u+v)+		=0
	3		27

	196		7
u3+v3+		+3(u+v)(uv−		)=0
	27		3

	196
u3+v3+		=0
	27

	7
uv−		=0
	3

	196
u3+v3=−
	27

	7
uv=
	9

	196
u3+v3=−
	27

	7
u3v3=[(		)3]/27
	3

	196
u3+v3=−
	27

	343
u3v3=[(		)]/27
	27

	196
u3+v3=−
	27

	343
u3v3=[(		)]
	729

__________ Czy do tego momentu jest ok ?

Mariusz: Jak nadążasz w szkole z programem i nie chcesz się ograniczać do tego co podadzą w szkole to możesz spróbować całkować Podstawy algebry ci nie zaszkodzą Jak pisałem liczby zespolone rozkład wielomianów na czynniki dzielenie wielomianów NWD wielomianów rachunek macierzowy dodawanie i odejmowanie macierzy mnożenie macierzy (tutaj przydaje się iloczyn skalarny) wyznacznik macierzy eliminacja Gaussa macierz odwrotna rozkład LU macierzy rząd macierzy (do twierdzenia Kroneckera Capellego) rozwiązywanie układów równań liniowych Później przydadzą się takie rozkłady jak diagonalizacja rozkład Jordana (do sprawnego potęgowania macierzy oraz do liczenia exponenty macierzy)

Mariusz: Tak jest ok We wzorach Vieta uważaj na znak przy sumie pierwiastków

Jerzy: Nigdy się nie chwaliłem, a tobie współczuję.

Mariusz: Założyłem że ten kolorowy Jerzy i ty to ta sama osoba

Jack: @zef Lepiej zebys sie zajal jednak prawdopodobienstwem i planimetria zamiast wzorow cardano. A jesli to opanowales to pocwicz dowody typu udowodnij ze dla kazdej liczby rzeczywistej... Na maturze Ci sie Cardano nie przyda a o punkty bedziesz walczyc

Mila: Jerzy jaki wpis?

Mariusz: Chciał całkować a z podstawień może mu wyjść całka która wymaga "wzorów Cardano" Poza tym te wzory działają na każde równanie i w przypadku gdy wyraz wolny i wyraz przy x³ ma sporo dzielników to nie zawsze sprawdzanie dzielników jest szybsze Jak nadąża z programem to zdąży Na pewno będą mieli powtórki

Mariusz: * na każde równanie trzeciego stopnia , sposób można uogólnić na równania czwartego stopnia

Mariusz: zef napisz o której będziesz Ja prawdopodobnie będe po 18:00 i możliwe że do południa chociaż nie jest to pewne

Mariusz: A teraz zagadka wiesz dlaczego udało mi się pokazać te wzory Cardano i Ferrariego ?

Mariusz: pokazać Vaxowi oczywiście

Zef: Bede dopiero dzisiaj po 18, teraz poza domem, dokoncze ten przyklad

zef: Jednak, nie znalazłem chwili czasu, ciągle pracuję poza domem i dopiero znajdę czas w poniedziałek.

jc: Mariusz, jakie znaczenie mają obecnie wzory na rozwiązanie równania 3 i 4 stopnia?

Mariusz: Po podstawieniu można otrzymać całkę której mianownik najlepiej rozłożyć z użyciem tych wzorów Widziałem kilka takich na forum na którym pisaliśmy z Vaxem Te wzory można pokazać licealiście bo można wyodrębnić tzw casus irreducibilis i rozwiązać go z użyciem trygonometrii omijając w ten sposób potrzebę wprowadzania liczb zespolonych Schemat całkowania funkcji wymiernych wymaga rozkładu mianownika na czynniki Czasami rozkład taki jest już podany ale gdy całkę z funkcji wymiernej dostaniemy po podstawieniu to już nie musi być podany

jc: Mariusz, spytam inaczej, komu obecnie potrzebne są wzory na rozwiązanie równań 3 i 4 stopnia? Całki, o których wspomniałeś, są zapewne pomylonymi zadaniami. Autor zadania lub ktoś przepisujący treść pomylił coś i wyszła całka wymagająca trudnego rozkładu na czynniki. Czy potrafiłbyś wskazać prawdziwy problem, gdzie wspomniane wzory się przydają? Jest tyle ważniejszych rzeczy w matematyce ...

Benny: Wzory może nie, ale rozwiązywanie takich równań jest przydatne przy wielomianach charakterystycznych chociaż jeszcze nie miałem takiego, aby nie dało się znaleźć pierwiastka wymiernego/całkowitego poprzez zwykłe zgadywanie.

jc: Benny, bo macierz została wymyślona tak, aby było prosto. Czy nauczyłbyś się więcej, gdyby było inaczej? Wzory Cardano są za to źródłem zadań typu: Czy liczba (5^1/2 + 2)^1/3 − (5^1/2 − 2)^1/3 jest wymierna ? To akurat ma jakiś sens.

6latek: Rownania stopnia trzeciego postaci x³+px+q=0 rozwiazuje sie bardzo latwo i przyjemnie metoda tablicowa sa rosyjsie tablice z 1950r .

Mariusz: Jeżeli chodzi o prawdziwą przydatność matematyki w ogóle to widziałem niedawno jeden dowcip Widziałem też drugi pokazujący myślenie matematyczne

jc: Mariusz, bardziej chodzi o to, że w pewnym wieku dobrze poznać wiele pojęć, pomysłów, niż doskonalić się w jednym obszarze. W wielu przypadkach lepiej jest zrozumieć, niż opanować schemat. Potem trudno przekonać się do nowych rzeczy. Czasem znów, ważniejsze jest (dobre) zdanie konkretnego egzaminu.

Mariusz: Skoro zef "pracuje poza domem" to raczej nie uda mu się przećwiczyć całkowanie Wątpię aby udało mu się przećwiczyć tematy które podała Mila no ale jak nadąża z programem to je przećwiczy (tematy które podała Mila) Całkowanie podobno wycięli ze szkoły średniej Jak ja chodziłem do średniej to całki pojedyncze jeszcze były Przypominam zef sam chciał całkować ale mało czasu chce na to przeznaczyć i może nic nie wyjść Z tematami podanymi przez użytkownika Mila jest podobnie tyle że będzie je miał w programie

Mariusz: Jeżeli chodzi o życie codzienne to matematyka mogłaby się skończyć na szkole podstawowej

zef:

	196		196
u3+v3=−		→u3=−		−v3
	27		27

	343
u3v3=
	729

	196		343
(−		−v3)(v3)=
	27		729

	196		343
−		v3−v6=
	27		729

podst. v³=t

	196		343
−t2−		t−		=0
	27		729

	196		343
t2+		t+		=0
	27		729

	38416		1372
Δ=		−
	729		729

	37044
Δ=
	729

	1372
Δ=
	27

Doszedłem do tego momentu, czy Cardano przyda mi się w liceum czy wystarczy "odgadywanie pierwiastków równania" ?

zombi: Oczywiście, że się nie przyda Warto znać dla samego faktu. Ja też policzyłem kilka przykładów w szkole średniej. I jeden na algebrze liniowej, bo jakiś potworny wielomian wyszedł.

Mariusz: Rozkład na mianownika na czynniki przydaje się przy rozkładaniu na sumę ułamków prostych zef proponuję abyśmy przeszli na gg czy na e−mail bo tu przeszkadzają Do tej pory dobrze

zef: Ale na gg czy mailu nie będzie można stosować tych matematycznych zapisów . Zostańmy tutaj

Mariusz: Można pisać sam kod texa albo ściągnąć ze strony forkosha mimetex i wysyłać wygenerowane w nim obrazki albo pobrać inny komunikator który ma wtyczkę do mimetexa (aqq,kadu) Jeśli chodzi o e−mail to tylko opcja z wtyczką odpada obrazki i kod texa możemy sobie przesyłać

zef: Warto się w to tak bawić ? Mi nie przeszkadzają jakoś posty innych

Mariusz: Skoro ci nie przeszkadzają to kontynuujmy Wyróżnik policzyłeś dobrze

Mariusz: Czy warto się tak bawić ? Będzie to przydatne gdy będziemy ćwiczyli rachunek macierzowy (tutaj nie mają macierzy) Szeregi i całki oznaczone też kiepsko wyglądają tutaj Szeregi przydają się nie tylko w analizie ale także w dyskretnej np funkcje tworzące które przekształcają ciąg w funkcję zdefiniowaną szeregiem którego współczynniki są kolejnymi wyrazami ciągu

Mariusz: Całką możesz policzyć pole powierzchni pod wykresem krzywej albo objętość bryły ograniczonej powierzchniami a wyznacznikiem możesz policzyć pole równoległoboku albo objętość równoległościanu

zef: Jak już chyba zauważyłeś umiem liczyć te "podstawowe" a nawet niektóre trochę trudniejsze całki, moglibyśmy przejść do obliczania zadań typu: oblicz pole powierzchni ograniczonej krzywymi:... itd, to mnie bardzo interesuje

Mariusz: To z algebry przećwiczmy chociaż NWD wielomianów bo może to się przydać w rozkładzie mianownika na czynniki a także podczas całkowania funkcji wymiernych w przypadku gdy mianownik posiada pierwiastki wielokrotne Chciałbym też przećwiczyć podstawienia Eulera bo przydatne będą w zadaniach takich jak Oblicz długość paraboli na odcinku (a,b)

Mariusz: Będę po 18:00 Jeśli będzie ci się nudziło to poczytaj http://matwbn-old.icm.edu.pl/kstresc.php?tom=15&wyd=10&jez=pl albo http://kielich.amu.edu.pl/Stefan_Banach/pdf/rachunek2.pdf

	3x8+24x7+181x6+602x5−554x4−9872x3−24106x2
∫		dx
	(x2+6x+10)2(x−2)2(x−1)(x2−8x+41)

	7960x+55240
+∫		dx
	(x2+6x+10)2(x−2)2(x−1)(x2−8x+41)

Mariusz: W tym przykładzie mianownik masz rozłożony na czynniki więc wystarczy zapisać całkę w postaci sumy funkcji wymiernej i całki z funkcji wymiernej W mianowniku funkcji podcałkowej zostawiasz tylko pojedyncze czynniki całki którą liczysz a w mianowniku funkcji wymiernej zostawiasz te same czynniki co w liczonej całce tyle że w potędze o jeden mniejszej Liczniki znajdujesz metodą współczynników nieoznaczonych pamiętając o tym że stopień licznika jest mniejszy od stopnia mianownika

	L(x)		L1(x)		L2(x)
∫		dx=		+∫		dx
	M(x)		(x2+6x+10)(x−2)		(x2+6x+10)(x−2)(x−1)(x2−8x+41)

Gdybym ten mianownik wymnożył to wtedy NWD wielomianów byłoby przydatne

Mariusz: "oblicz pole powierzchni ograniczonej krzywymi:... itd, to mnie bardzo interesuje" Najpierw powinieneś dobrze opanować całki nie oznaczone ponieważ istnieje coś takiego jak Twierdzenie Newtona Leibniza Całka oznaczona to różnica funkcji pierwotnych na krańcach przedziału Gdybyś chciał liczyć całkę oznaczoną z definicji to musiałbyś liczyć granicę z pewnej sumy a to nie zawsze jest dobry pomysł

Mariusz: * trochę niepotrzebnie spacja mi się wcisnęła w słowie nieoznaczone

zef: Mając całkę złożoną z 2 wielomianów gdzie stopień licznika jest wyższy należy ją podzielić w taki sposób żeby wyszedł jakiś w(x) (ze stopniem niższym niż początkowy stopień licznika) oraz jakaś reszta r(x). Ale zastanawia mnie czemu nie napisałeś że te w(x) − w twoim przypadku L₁(x)− nie jest całkowane ? I co w przypadku jakby to była całka oznaczona, może po prostu zapomniałeś dopisać tej całki albo ja czegoś nie rozumiem.

Mariusz: Nie zapisałem dokładnie jak powinny wyglądać liczniki bo tu nie mają texa i zapis mógł się "rozjechać" Ostrogradski zauważył że funkcja wymierna właściwa (stopień licznika jest mniejszy od stopnia mianownika) jest składnikiem funkcji pierwotnej gdy mianownik funkcji podcałkowej zawiera pierwiastki wielokrotne (mogą być zespolone) Przedstawiamy więc całkę jako sumę funkcji wymiernej i innej całki z funkcji wymiernej w której mianownik zawiera już tylko pierwiastki pojedyncze Krotność czynników mianownika funkcji wymiernej jest o jeden mniejsza niż krotność czynników mianownika funkcji podcałkowej

	3x8+24x7+181x6+602x5−554x4−9872x3−24106x2
∫		dx
	(x2+6x+10)2(x−2)2(x−1)(x2−8x+41)

	7960x+55240
+∫		dx=
	(x2+6x+10)2(x−2)2(x−1)(x2−8x+41)

a2x2+a1x+a0
	+
(x2+6x+10)(x−2)

	b5x5+b4x4+b3x3+b2x2+b1x+b0
∫		dx
	(x2+6x+10)(x−2)(x−1)(x2−8x+41)

Różniczkujesz stronami i obliczasz współczynniki liczników Tutaj akurat rozkład mianownika na czynniki miałeś podany ale gdybym ten mianownik wymnożył to NWD wielomianów byłoby przydatne

Mariusz: Całkę po lewej przedstawiłem w postaci sumy dwóch całek bo tu nie mają texa i zapis by się "rozjechał"

zef: Niestety mało rozumiem z czystej teorii.. Mógłbyś pokazać mi jakiś przykład z tym związany w pełni rozwiązany ?

Mariusz:

	dx		a3x3+a2x2+a1x+a0		b1x+b0
∫		=		+∫		dx
	(x2+1)3		(x2+1)2		x2+1

1
	=
(x2+1)3

(3a3x2+2a2x+a1)(x2+1)2−(a3x3+a2x2+a1x+a0)(x2+1)4x
(x2+1)4

	b1x+b0
+
	x2+1

1
	=
(x2+1)3

(3a3x2+2a2x+a1)(x2+1)−4x(a3x3+a2x2+a1x+a0)
	+
(x2+1)3

(b1x+b0)(x2+1)2
(x2+1)3

1=(3a₃x²+2a₂x+a₁)(x²+1)−4x(a₃x³+a₂x²+a₁x+a₀)+ (b₁x+b₀)(x⁴+2x²+1) 1=(3a₃x⁴+2a₂x³+a₁x²+3a₃x²+2a₂x+a₁)− (4a₃x⁴+4a₂x³+4a₁x²+4a₀x)+(b₁x⁵+2b₁x³+b₁x+b₀x⁴+2b₀x²+b₀) 1=b₁x⁵+(b₀−a₃)x⁴+(2b₁−2a₂)x³+(2b₀+3a₃−3a₁)x²+ (b₁+2a₂−4a₀)x+(a₁+b₀) b₁=0 b₀−a₃=0 2b₁−2a₂=0 2b₀+3a₃−3a₁=0 b₁+2a₂−4a₀=0 a₁+b₀=1 b₁=0 b₀=a₃ a₂=0 5a₃−3a₁=0 a₀=0 a₃+a₁=1 b₁=0 b₀=a₃ a₂=0 a₀=0 5a₃−3a₁=0 3a₃+3a₁=3 b₁=0 b₀=a₃ a₂=0 a₀=0 8a₃=3 8a₁=5

	dx		1	3x3+5x		3		dx
∫		=			+		∫
	(x2+1)3		8	(x2+1)2		8		x2+1

	dx		1	3x3+5x		3
∫		=			+		arctan(x)+C
	(x2+1)3		8	(x2+1)2		8

Kolejny przykład to wpis z 23 kwi 11:15 na stronie https://matematykaszkolna.pl/forum/323858.html

Mariusz: Całkowanie funkcji wymiernych

	L(x)
∫		dx
	M(x)

1. deg L(x) ≥ deg M(x) L(x)=M(x)W(x)+R(x)

	L(x)		R(x)
∫		dx=∫W(x)dx+∫		dx
	M(x)		M(x)

2. deg L(x) < deg M(x) ⋀ gcd(M(x),M'(x))≠const

	R(x)		R1(x)		R2(x)
∫		dx=		+∫		dx (*)
	M(x)		M1(x)		M2(x)

M₁(x)=gcd(M(x),M'(x)) M(x)=M₁(x)M₂(x) deg R₁(x)<deg M₁(x) deg R₂(x)<deg M₂(x) Liczniki R₁(x) oraz R₂(x) znajdujemy metodą współczynników nieoznaczonych Przyjmujemy za współczynniki tych wielomianów współczynniki literowe i rożniczkujemy obustronnie równość (*) aby je obliczyć 3. deg L(x) < deg M(x) ⋀ gcd(M(x),M'(x))=const

	R2(x)
∫		dx
	M2(x)

Niech M₂(x)=(x−a₁)(x−a₂)*...*(x−a_k) (x²+p₁x+q₁)(x²+√2x+q₂)*...*(x²+p_mx+q_m)

	R2(x)		A1		A2		Ak
∫		dx=∫		dx+∫		dx+...+∫		dx
	M2(x)		x−a1		x−a2		x−ak

	B1x+C1		B2x+C2
+∫		dx+∫		dx
	x2+p1x+q1		x2+p2x+q2

	Bmx+Cm
+...+∫		dx
	x2+pmx+qm

Podstawienia sprowadzające całki do całek z funkcji wymiernej ∫R(x,√ax²+bx+c)dx R(x,y) − funkcja wymierna dwóch zmiennych 1. a>0 √ax²+bx+c=t−√ax ax²+bx+c=t²−2√atx+ax² bx+c=t²−2√atx 2√atx+bx=t²−c x(2√at+b)=t²−c

	t2−c
x=
	2√at+b

	2√at2+bt−√at2+√ac
√ax2+bx+c=t−√ax=
	2√at+b

	√at2+bt+√ac
√ax2+bx+c=
	2√at+b

	2t(2√at+b)−2√a(t2−c)
dx=		dt
	(2√at+b)2

	√at2+bt+√ac
dx=2		dt
	(2√at+b)2

	t2−c		√at2+bt+√ac		√at2+bt+√ac
∫R(		,		)2		dt
	2√at+b		2√at+b		(2√at+b)2

∫R₁(t)dt 2. a<0 Tutaj możemy założyć że b²−4ac>0 inaczej trójmian kwadratowy przyjmowałby tylko wartości ujemne √ax²+bx+c=(x−x₁)t √a(x−x₁)(x−x₂)=(x−x₁)t a(x−x₁)(x−x₂)=(x−x₁)²t² a(x−x₂)=(x−x₁)t² ax−ax₂=xt²−x₁t² ax−xt²=ax₂−x₁t² x(a−t²)=ax₂−x₁t²

	ax2−x1t2		ax2−ax1+ax1−x1t2
x=		=
	a−t2		a−t2

	ax2−x1t2		x2−x1
x=		=x1+a
	a−t2		a−t2

	(x2−x1)t
√ax2+bx+c=(x−x1)t=a
	a−t2

dx=−a(x₂−x₁)(a−t²)⁻²2tdt

	t
dx=−2a(x2−x1)		dt
	(a−t2)2

	ax2−x1t2		t		t
∫R(		,a(x2−x1)		)(−2a(x2−x1)		)dt
	a−t2		a−t2		(a−t2)2

∫R₃(t)dt Te podstawienia powinny wystarczyć do sprowadzenia całek postaci ∫R(x,√ax²+bx+c)dx do całek z funkcji wymiernej ale czasami podstawienie √ax²+bx+c=xt+√c prowadzi do całki wymagającej mniej obliczeń o ile wyraz wolny trójmianu kwadratowego jest większy od zera Całki postaci ∫x^m(a+bxⁿ)^pdx p∊Z Podstawienie t^α=x , α=nww(m,n) sprowadzi całkę do całki z funkcji wymiernej 2.

m+1
	∊Z
n

	r
Niech p=
	s

Podstawienie t^s=(a+bxⁿ) sprowadzi całkę do całki z funkcji wymiernej

m+1
	+p∊Z
n

	r
Niech p=
	s

	a+bxn
Podstawienie ts=
	xn

sprowadzi całkę do całki z funkcji wymiernej Całki postaci ∫R(e^x)dx Tutaj podstawienie t=e^x sprowadzi całkę do całki z funkcji wymiernej Do tej postaci można sprowadzić całki ∫R(sinh(x),cosh(x))dx Całki postaci ∫R(sin(x),cos(x))dx

	x
t=tan(		)
	2

	x   sin( )   2
t=
	x   cos( )   2

	1   x   1   x   cos2( )+ sin2( ) 2   2   2   2
dt=		dx
	x   cos2( )   2

	1		x
dt=		(1+tan2(		))dx
	2		2

	1
dt=		(1+t2)dx
	2

2dt=(1+t²)dx

	2
dx=		dt
	1+t2

	x   sin2( )   2
t2=
	x   cos2( )   2

	x   x   sin2( )+cos2( )   2   2
t2+1=
	x   cos2( )   2

	1
t2+1=
	x   cos2( )   2

	x		1
cos2(		)=
	2		t2+1

	x		x		1		t2
sin2(		)=1−cos2(		)=1−		=
	2		2		t2+1		t2+1

	1		t2		1−t2
cos(x)=		−		=
	t2+1		t2+1		1+t2

	2t
tan(x)=
	1−t2

sin(x)		2t
	=
cos(x)		1−t2

	sin(x)
sin(x)=		cos(x)
	cos(x)

	2t	1−t2		2t
sin(x)=			=
	1−t2	1+t2		1+t2

	2t		1−t2		2
∫R(		,		)		dt
	1+t2		1+t2		1+t2

∫R(t)dt Argument tangensa można przesunąć o dowolną stałą i nadal to podstawienie będzie sprowadzać całki postaci ∫R(sin(x),cos(x))dx do całek z funkcji wymiernej tzn zamiast podstawienia

	x		x
t=tan(		) można równie dobrze podstawić t=tan(		+φ)
	2		2

gdzie φ=const

Mariusz: Zamiast wydzielać część wymierną całki możesz także skorzystać z wzoru redukcyjnego na całkę

	1
∫		dx
	(1+x2)n

Spróbuj go sobie wyprowadzić