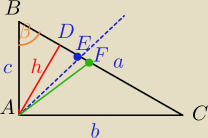
trójkąt prostokatny matma_na: Mamy trójkąt prostokąny ABC o kącie A = 90^o oraz AB < AC. Niech D, E, F lezą na boku BC tak ze AD jest wysokością, AE jest wenetrzną dwusieczną, oraz AF jest srodkową. Jak pokazać ze 3AD + AF > 4AE.

matma_na: Czy można zakładać w takim zadaniu ze np AC=1

6latek: ja mysle ze nie wolno tak zakladac

Programista: Możesz, ale w niczym to nie pomoże.

matma_na: no to można czy nie można w koncu?

6latek: matma _na czy Ty teraz chodzisz do 1 klasy liceum czy skoczylas 1 klase . Pytasz sie o takie rzeczy o ktore powinnas zapytac swojego nauczyciekla czy w zadaniach na dowodzenie czy w stylu wykaz ze mozesz sobie przyjmowac dowolne wartosci

matma_na: Ale tylko czy moge podstawić za AC=1 za reszte juz nie

6latek: Wedlug mnie jesli nie ma tego wyraznie napisane w tresci to nie mozna podstawiac

6latek: Poczekaj jeszcze moze ktos sie wypowie Ja na Twoim miejscu zrobilbym porzadny rysunek do zadania Nastepnie poczytal o srodkowej w trojkacie prostokatnym (czemu jest rowna ) i np wysokosci (jak dzieli przeciwprostokatna

matma_na: Wiem że środkowa w trójkącie prostokątnym dzieli trójkąt na dwa trójkąty równoramienne.

matma_na:

	ab
Wiem ze wysokość h=
	c

omikron: Nie możesz podstawiać dowolnej wartości, jak nie jest ona dana w poleceniu, jedyne co możesz zrobić to oznaczyć sobie AC jako np. x.

Mila: Z jakiego zbioru masz to zadanie? Z której klasy?

Mila:

	1
|AF|=		a
	2

	b*c√2
|AE|=
	b+c

c*b=a*|AD|

	c*b
|AD|=
	a

	c*b		1		b*c*√2
3*		+		a> ?4*
	a		2		b+c

spróbuj wyrazić b i c za pomocą przeciwprostokątnej a i funkcji tryg. kąta β. β∊(45^o,90^o)

matma_na: A nie można za AC=1 i wtedy by było łatwiej?

Saizou : nie można, wtedy ograniczasz się do grupy trójkątów prostokątnych o przeciwprostokątnej o dł. 1 ale moja rada jest taka: jak zrobisz to dla dł. AC=1 (czyli konkretnego przypadku), pomyśl nad uogólnieniem tego

Mila: Jeżeli zrobisz tak, jak napisałam 20:24, to przez a będziesz mogła uprościć i po kłopocie.

matma_na: Mila tzn jak wyrazić te b i c

Mila: Nie wiem po której klasie jesteś, zatem nie wiem jaki masz zakres przerobionego materiału. Napisz to poradzę.

matma_na: no teraz już w trzeciej bede

jc: Mila, to nie taka prosta sprawa z tą nierównością z 20:24. Mam ją już od kilku godzin. 3 ab/c + c/2 > 4√2 ab/(a+b) Przeciwprostokątną wolę oznaczyć literą c. L ≥ √ab√6, P ≤ √8 √ab, niestety 8 > 6. Wygląda na to, że warunek a²+b² = c² jest bardzo ważny.

Mila: Witaj JC. Nie jest prosta, wprowadzając uzależnienie za pomocą dł. przeciwprostokątnej i sinβ, cosβ też mam nierówność z funkcją trygonometryczną. Dlatego pytam z jakiego poziomu zadanie, może inny sposób trzeba znaleźć.

Mila: matma_na wg oznaczeń 20:24

	b
sinβ=		⇔b=a*sinβ
	a

	c
cosβ=		⇔c=a*cosβ
	a

Z jakiego zbioru zadanie?, Czy maturalne?

matma_na: Mam kesrówki zadań ze szkoły na wakacje i nie jest napisane skąd. A czy jakies bardzo jest ono trudne?

Mila: Wpisz poprzednie zadanie z tej kserówki, może są powiązane jakimś twierdzeniem , które mi nie przychodzi do głowy w tej chwili. Nierówność trygonometryczną da się rozwiązań. Może jednak jest łatwiejszy sposób.

matma_na: poprzednie miałem to https://matematykaszkolna.pl/forum/329101.html

jc: Jak rozwiążemy, wyjaśni się, czy zadanie było trudne. Przy okazji, Mila, wczoraj, może przedwczoraj, pojawiło się zadanie, z którym sobie nie poradziłem. https://matematykaszkolna.pl/forum/329059.html Może Ty dasz radę

matma_na: https://matematykaszkolna.pl/forum/329059.html to chyba nie mój poziom

jc: To była propozycja dla Mili.

matma_na: A mozecie zerknąć na moje zadanie bo to juz chyba rozwiązane jest

jc: Mam straszne rozwiązanie. s² + t² ≥ 2st (*) √s² + t² ≥ √2√st s + t ≥ 2 √st (*) (s+t) √s² + t² ≥ 2 √2 st

1		1		2√2
	+		≥
s		t		√s2+t2

Podstawiam s = √a²+b² = c, t =√2ab

1		1		2√2
	+		≥
c		√2ab		a+b

2ab		ab
	+ √2ab ≥ 4√2
c		a+b

ab		c
	+		≥ √2ab (*)
c		2

3ab		c		ab
	+		≥ 4√2
c		2		a+b

(3 razy korzystam z nierówności pomiędzy średnimi, zaznaczyłem *)

Mila: Ja rozwiązałam równanie trygonometryczne, ale też wredne i dlatego nie napisałam. Myślę, że jest prostszy sposób, na pewno wymyślimy. Pozdrawiam