geometria matma_na:

	3
Pokaż ze w dowolnym trójkacie suma dowolnych dwóch środkowych jest nie wiąksza niż
	4

obwodu.

Metis: Przydałaby się η

6latek: A moze Yeti

Metis: Jak zwą , tak zwą

matma_na: co>>

Metis: O Yetim nie słyszałeś?

matma_na: to zarty sa na tym forum?

Metis: Także

Jack: aj, udalo mi sie jedynie wykazac ze suma dlugosci wszystkich srodkowych jest wieksza od

	3
		obwodu.
	4

6latek: ABC to wierzcholki trojkata oraz wektory a b c odpoweidnio wektory AB BC CA Zauwazamy ze a+b+c=AB+BC+CA=0 (wektory bede je oznacal * Podnosimy ta rownosc sklalarowo do potegi drugiej − mamy (a^*+b^*+c^*)²= a^2*+b^2*+c^2*+2(a^*b^*+b^*c^*+c^*a^*)=0 a^*b^*+b*c^*+c^*a^*=−0,5(a²+b²+c²) Srodkowa p= a^*+0,5b^* srdkow q = b^*+0,5c^* i r=c^*+0,5a^* Podnosimy te wsektory skalrowo do potegi drugiej mamy p²⁸=a²+0,25b²_a^*b^* q^2*= b²+0,25c²+b^*c^* r^2*= c²+0,25a²_c^*a^* Dodajemy stronami te rownania i zastepujemy tez a^*b^*+b⁸c^*+c^*a^*=−0,5 (a²+b²+c²)

	5
mamy p2+q2+r2=		(a2+b2+c2)+a*b*+b*c8+c*a*=
	4

5		1		3
	(a2+b2+c2)−		(a2+b2+c2)=		(a2+b2+c2)
4		2		4

czyli p²+q²+r²= 0,75(a²+b²+c²) Tutaj udowdnilismy ze suma kwadratow srodkowych trojkata jest rowna 0,75 sumy kwadratow bokow tego trojkata

6latek: Ajjj mielismy wykazac ze same dlugosci nie kwadraty dlugosci

Metis: Może Saizou się skusi ?

Jack: witaj, no i to dwoch a nie wszystkich trzech

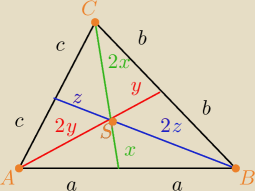
Jack: z nierownosci trojkata w : ΔASC : 2y + 2x > 2c x + y > c ΔASB 2y + 2z > 2a y + z > a ΔBSC 2x + 2z > 2b x + z > b

	3		3		3
Nasz obwod to 2a+2b+2c zatem		obwodu to		* 2 * (a+b+c) =		(a+b+c)
	4		4		2

dodajac nierownosci

	3
2x + 2y + 2z > a + b + c //*
	2

	3
3x + 3y + 3z >		(a + b + c)
	2

	3
stad wiemy ze suma dlugosci wszystkich srodkowych jest wieksza od		obwodu.
	4

hmm chyba nie tego szukalismy ale wkleje zeby bylo, a co mi tam...

6latek: Witaj Jack

matma_na:

	3
Mam jeszcze pokazać ze suma dwóch środkowych jest nie mniejsza niż		obwodu.
	8

Moze ktoś pokazać jedno z nich. Fajnie by było jak by były te dwa dowody.

jc: Twierdzenie jest równoważne ze stwierdzeniem, że zielona droga jest dłuższa od czerwonej. Wydaje się, że tak jest (zieloną drogą idziemy bardziej na około).

matma_na: A da sie przeproadzić jakis formalny dowód ,czy to zadanie jest trudne bardzo?

janoski: To zadanie na poziomie szkoły sredniej czy juz wyzej ?

matma_na: srednia szkkoła

6latek: Z tw cosinusow mamy uklad rownann {b²=a²+c²−2ac cosβ

	a2
{m12=		+c2−accosβ
	4

Z tego ulkadu masz ze m₁= 0,5(√2b²+2c²−a² Tak samo wylicz dlugosc srodkowej m₂ dodaj to i zobacz co wyjdzie (najwyzej wyjdzie zle .

matma_na: nu druga jest analogiczna ale co dalej /

6latek: Jest analogiczna tzn jaka?

jc: Zamień małe litery na duże Twierdzenie jest równoważne z nierównością AS + SB ≤ AD + DF + FB (podstaw i zobaczysz: AS = 2/3 AF, BS = 2/3 BD, AD = AC/2 , BF=BC/2, DF=AB/2) AD +DF ≥ AF = AS + SF SF + FB ≥ SB Dodajesz stronami, redukujesz SF i masz wynik.

matma_na: 0,5(2a²+2c²−b²)^1/2

6latek: jc a to co ja proponuje to jest zle ? czxy moz ejest wiecej liczenia ?

matma_na: AD +DF ≥ AF = AS + SF SF + FB ≥ SB tutaj dodawać stronami?

matma_na: czyli ze AD+DF+FB≥AS+SB ?

jc: Tak Ojej... Mała pomyłka. Powinno być: Twierdzenie jest równoważne z nierównością AS + SB ≥ AD + DF + FB

matma_na: jc dzieki a z podpunktem b) jak sobie poradzic

	3
Mam jeszcze pokazać ze suma dwóch środkowych jest nie mniejsza niż		obwodu.
	8

jc: Trochę pokręciłem AD +DF ≥ AF = AS + SF FB +SF ≥ SB stąd AD+DF+FB ≥ AS + SB A więc (AB+BC+CA)/2 ≥ (2/3) (AF + BD) czyli AF + BD ≤ (3/4) (AB+BC+CA)

jc: Niestety mam inną pilną sprawę ... Jutro po południu

jc: Spróbujmy tak AB ≤ AS + SB AD ≤ AS + SD BF ≤ BS + SF drugie i trzecie mnożymy przez 2 i wszystko dodajemy AB + BC + CD ≤ (3 AS + 2SF) + (3 BS+2SD) = (2+2/3) (AF + BD) = (8/3) (AF+BD) czyli AF + BD ≥ (3/8) (AB + BC + CD) Udało się

matma_na: Super jestes WIELKI