prawdo model matematyczny: szesc ponumerowanych kul rozmieszczamy w piesciu ponumerowanych szufladach oblicz prawdopodobienstwo ze w kazdej szufladzie bedzie co najmniej 1 kula

	5 1	6 2
ciekawi mnie moc A ale obliczona w inny sposób tzn rozwiazanie z ksiazki A=			*4!

chciałbym to rozpisac tak aby zamiast 4! był zapis taki (4⁴ −4) − i dalej nie wiem

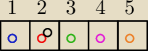
Mila: 1) Twój zapis 4⁴−4 tutaj nie może być zastosowany. 4⁴− liczba wszystkich ciągów 4−wyrazowych utworzonych ze zbioru 4 elementów. 2) |Ω|=5⁶ liczba wszystkich ciągów 6− wyrazowych ze zbioru 5 elementów A− w każdej szufladzie znajdzie się co najmniej jedna kula f:{k₁,k₂,k₃,k₄,k₅,k₆}→{s₁,s₂,s₃,s₄,s₅} Na ilustracji masz jedno ze zdarzeń : W każdej szufladzie ma być co najmniej 1 kula , zatem w jednej z szuflad znajdą się 2 kule.

5 1
	wybór szuflady do której włożymy dwie kule .

6 2
	−wybór dwóch kul , które znajdą się w wybranej szufladzie

4!− permutacja pozostałych.

6 2
	*5!

======

Jerzy: Wiedziałem Milu , że Ty to dzisiaj rozwiążesz.... *10²

Mila: No mogłam nie zdążyć.

PW: Obliczenie mocy zdarzenia A − "W każdej szufladzie znajdzie się co najmniej jedna kula" w tym zadaniu oznacza obliczenie mocy zdarzenia "W jednej z szuflad znalazły się dwie kule i w pozostałych czterech − po jednej kuli".

	6 2
Wybieramy więc dwie spośród sześciu kul − możemy to zrobić na		sposobów. Następnie ten

element złożony z dwóch kul (zbiór, nie uwzględniamy kolejności) rozmieszczamy razem z pozostałymi czterema kulami w pięciu szufladach, tak by w każdej znalazł się jeden element (dwie wybrane kule albo dowolna z czterech pozostałych). Tworzenie elementów zbioru A jest więc dwuetapowe − najpierw wybór dwóch kul, potem permutacja pięciu elementów.

	6 2
|A| =		·5!

Liczba jest taka sama jak podajesz za podręcznikiem, ale sposobu liczenia:

	5 1	6 2
			4!

na podstawie samego wzoru nie rozumiem.

Jerzy: Musiałbym długoooo... myśleć, a to mi dzisiaj nie pasuje

PW: Aaa..., Mila jak zwykle była inteligentniejsza ode mnie

Jerzy: You're simply the best

Mila: PW, miałam zamiar rozwiązać tak, jak Ty, ale wyjaśniłam sposób "książkowy". Pozdrowienia dla obu Panów

model matematyczny: wiecie bo ogólnie myślałem, że jest to sytuacja symetryczna do tej https://matematykaszkolna.pl/forum/192088.html tu od ETY a tutaj od Mili i PW :https://matematykaszkolna.pl/forum/285288.html ale najwyraźniej nie jest....

model matematyczny: "tam też się odejmowało te złe rozmieszczenia"

Mila: Tu masz wyjątkowo przyjazne liczby kul i szuflad. Tamtym sposobem byłoby skomplikowane . Liczba suriekcji:

5 0		5 1		5 2		5 3		5 4		5 5
	*(5−0)6−		*(5−1)6+		*(5−2)6−		*(5−3)6+		*(5−4)6+		*(5−5)6

Zatem nie ma sensu komplikować sobie życia.

model matematyczny: no a tak w maksymalnym uproszczeniu co się teraz stało ? bo patrzę na to co napisałaś i nie rozumiem

Mila: Nie przejmuj się, na studiach wytłumaczą. Jednak zawsze kierujemy się zdrowym rozsądkiem, rozwiązuj takie zadanie sposobem PW, albo tym z książki.