nierówność aro400: Rozwiąż nierówność:

6x		12x		12x
	− √		− 24√		>0
x−2		x−2		x−2

Eta:

	12x
1/ założenia :		≥0 i x−2≠0 ⇒ x ............
	x−2

2/ zastosuj podstawienie:

	12x		12x		12x
4√		= t , t≥0 to		= t4 i √		= t2
	x−2		x−2		x−2

	6x		1		12x		1
to		=		*		=		t4
	x−2		2		x−2		2

	1
nierówność przybiera postać :		t4−t2−2t>0
	2

.......................... i działaj ( pamiętaj o założeniu!

mietek: Jako, że nie można tworzyć nowych tematów, to przywłaszczę sobie ten Mam zadanie o treści "rozwiąż układ równań. podaj jego interpretację geometryczną" x² + y² − 6x − 7 = 0 y = x + 1 rozwiązać potrafię, ale "interpretacja geometryczna" brzmi obco.. cóż to takiego?

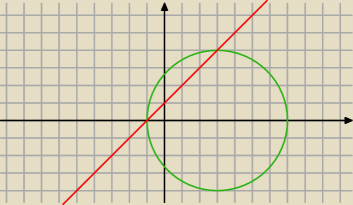
Jerzy: pierwsze równannie to okrąg, drugie to prosta....zrób rysunek i zinterpretuj

Janek191: Narysuj okrąg i prostą .

mietek: na czym polega interpretacja (po narysowaniu okregu i prostej)?

Jerzy: opisz, jak jest położona ta prosta względem okręgu

Jerzy:

mietek: więc rysuję i określam czy 1) nie jest styczna 2) jest styczna 3) ma 2 pkty wspólne z okręgiem?

mietek: a jakbym miał takie zadanie, ale nie byłoby okreŋu, a 2 proste.. to określam tylko czy mają pkty wspólne czy coś jeszcze?

rs: Jak obliczyć pole równoległoboku mając przekątne i 1 krótszy bok ? Jakaś podpowiedź ?

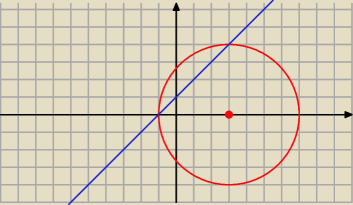
Janek191: (x −3)² − 9 +( y − 0)² − 7 = 0 (x −3)² + ( y − 0)² = 4² oraz y = x + 1 Interpretacja : Punkty wspólne: A = ( − 1 , 0) i B = ( 3, 4) ================================

Jerzy: dokładnie tak .... prosta przecina okrąg w puntach: ( wypisz te punkty )

Jerzy: tak .. rysujesz te dwie proste

aro400: Dziękuję za rozwiązanie Eta

mietek: Ok, rozumiem − dzięki Wam rs − ja skradłem ten temat, znajdź sobie własny

Janek191:

rs: Oj cicho Ja tu tylko na chwilę potrzebuję podpowiedzi z geometri której nienawidzę. Zadanie jest proste ja mam bok równoległoboku i podane przekątne, wie ktoś jak pole obliczyć ?

rs: Szukałem zadanka na necie i jest jedynie z wykorzystaniem twierdzenia cosinusów, a tego jeszcze nie przerabialiśmy więc musi być prostszy sposób. Dany jest równoległobok o krótszym boku 6cm. Przekątne 8 i 12, oblicz pole

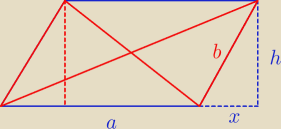
Janek191: Dane: b, p₁, p₂ gdzie p₁ > p₂ Oblicz : h i a ( a + x)² + h² = p₁² b² = x² + h² (a − x)² + h² = p₂²

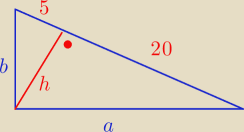
Krzychu: cześć szkoda że nie można dodawać tematów a mam do rozwiązania trochę zadań proszę o pomoc 1. Oblicz pole trójkąta prostokątnego jeżeli wysokość dzieli przeciwprostokątną na odcinki 5cm i 20cm 2.Trójkąt prostokątny wpisany w okrąg o promieniu 10cm i przyprostokątnej 12cm jest podobny do trójkąta o polu 6cm² oblicz a) skalę prawdopodobieństwa b)obwód mniejszego trójkąta

rs: 1. h=√x*y gdzie x i y to części tej przeciwprostokątnej czyli 5i 20

Janek191: h² = 5*20 = 100 h = 10 P = 0,5*25*10 = 125 [j²]

Janek191: z.2 Skala podobieństwa

rs: Okej Janek dzięki wielkie po porównaniu tego do rysunku rozumiem już wszystko, ale zadanie wydaje sie byc latwe, nie da sie go zrobic inaczej ?

Janek191: z.2 c = 2 r = 20 cm a = 12 cm b = 16 cm P_Δ = 0,5*12*18 = 108 [cm²]

PΔ		108
	=		= 18 = k2 ⇒ k = 3√2
PΔ'		6

mietek: rs − tego nawet nie trzeba rysować.. jest wzór w tablicach na dole 8 strony

Janek191: L = a + b + c = 12 + 16 + 20 = 48

	48		8*2
L' = 48 : k =		=		= 8√2
	3√2		√2

Krzychu: 3. Oblicz pole trójkąta wiedząc żę promień okręgu wpisanego w trójkąt ma 3cm b)promień okręgu opisanego ma 12cm

Eta: Jakiego trójkąta?

Krzychu: równobocznego

gosciu: Widze ze nie mozna dodawac nowych zadan, wiec podczepie sie do tego tematu. Rozwiaz rownanie trygonometryczne: sin³x + cos³x = 1 Doszedlem do takiego momentu: sin³x + cos³x = sin²x + cos²x sin²x(sinx−1) = cos²x(1−cosx) Jakies pomysly jak to dalej poprowadzic zeby doprowadzic do postaci iloczynowej? Poprawna odpowiedz: x=2kπ v x=^π₂+2kπ Bede wdzieczny za kazda pomoc

Krzychu: chciałbym naprawdę umieć samemu rozwiązywać te zadania czemu mając nawet wzory ciężko to tak idzie?

Eta:

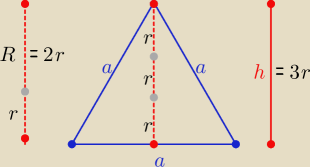
	a√3		a√3		a√3
r=		i 2r=R=		bo h=
	6		3		2

1 / r=3 to a√3=6r ⇒ a=6√3

	1
to P=		*a*3r=.....
	2

2/ podobnie R=2r=12 ⇒ r=6 itd...............................

Eta: I jak Krzychu?

5-latek : Dzien dobry Jakos leci do przodu .

Krzychu: 1. 0,5 * 6√3 * 9=27√3 ?

Eta: 1/ ok 2/ P=............ ?

Krzychu: nie wiem czemu ale wydaje mi się że wyjdzie to samo albo 54√3

kotek: Planimetria wykaż, że... http://scr.hu/2pxl/rmc92

kotecek: ktoś pomoże?

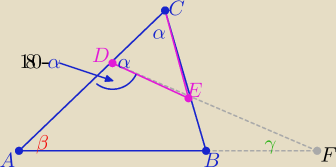
Eta: Z treści zadania ΔCED jest równoramienny to wprowadź odpowiednie oznaczenia miar kątów ......................... W ΔADF ; β+180⁻α+γ=180^o ⇒ α=β+γ co kończy dowód

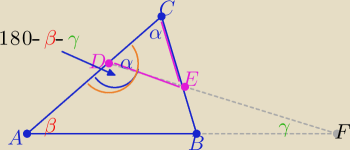
Eta: 2 sposób ..Wpisz oznaczenia miar kątów podobnie jak poprzednio............................ ................................ to 180^o−β−γ+α=180^o ⇒ α=β+γ c.n.u

Krzychu: tak sobie liczę te zadanka... chcę wiedzieć czy dobrze to rozwiązałem W trójkącie prostokątnym przyprostokątne mają 3 i 4 cm 1.oblicz pole trójkąta 2.oblicz długość wysokośći wychodzącej z wierzchołka kąta prostego 1. a=3 b=4 to c=5 liczę połowę obwodu 3+4+5/2= 6 następnie stosuję wzór herolda. p=6*3*2*1=36 pole= 36 ?

mietek: Szybkie pytanko potrzebne do zadania nad którym pracuje − czy 2 proste nie mają pkt wspólnych jeżeli mają te same a, a różne b?

Krzychu: i jak dobrze ?

5-latek : Mietek dwie proste nie maja punktów wspólnych kiedy sa rownolegle i nie nakladaja się na siebie wiec ?

mietek aka Herold: czyli jest tak jak napisałem.. chyba

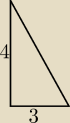
5-latek : Krzychu po co do pola tego trojkata Heron ? a=3 h=4 P= 0,5*a*h = 6 Przy wzorze Herona jest pierwiastek wiec √36=6

5-latek : tak Mieciu . tak jak napisales

mietek:

Krzychu: przepraszam zapomniałem napisać pierw z 36 = 6 ważne że dobrze

Krzychu: W trójkącie prostokątnym przyprostokątne mają 3 i 4 cm oblicz długość wysokośći wychodzącej z wierzchołka kąta prostego

mietek:

	ab
hc =
	c

Krzychu: 6√3 ?

Krzychu: mieciu wysokość mi wyszła 6√3

5-latek : Wedlug tego wzoru to jakim cudem ? Po drugie wiesz dlaczego taki wzor ? Jeśli nie to dlaczego nie dopytasz mietka ?

kotecek: dziękuje Eta

mietek: Krzychu, zrób tak jak mieciu i zaprzyjaźnij się z tablicami, bo warto a i b to przyprostokątne, a więc 3 i 4 przeciwprostokątna to √3² + 4² = √25 = 5 (z pitagorasa..)

	3*4		12
więc otrzymujemy		=		.. nie wiem jak Ci wyszło 6√3
	5		5

Allel: Uczeń ma przeczytać ksiązke ktora ma 380 str pierwszego dnia przeczytal 10 str a potem co nastepny dzien czytal o 4 str wiecej kiedy przeczyta ksiazke ? Z ciagu atytemtycznego blagam pomocy

mietek: to by chyba było jakoś tak a_n = 10 + 4(n−1) 10 + 4(n−1) = 380 itd...

mietek: stop... nie tak w ten sposób obliczylibyśmy, którego dnia przeczyta 380 stron to trzeba policzyć ze wzoru na sumę

Allel: pokazalbys mi jak ?

mietek: a_n = 10 + 4(n−1) = 4n + 6

	a1 + an		10 + 4n + 6
Sn =		* n =		* n =
	2		2

	4n + 16
=		* n = n(2n+8) = 2n2 + 8n
	2

2n² + 8n = 360 2n² + 8n −360 = 0 n² + 4n − 180 = 0 teraz Δ i ... n=2(√46−1) ≈ 11,5 tylko to troche dziwna sprawa, bo n∊N₊ w ciągach... ale to pewnie dlatego, że na ostatni dzień zostało troche mniej stron niż czytelnik był w stanie przeczytać... ale to lepiej niech się wypowie ktoś kto się na tym zna

Eta: 380 stron a nie 360

5-latek : a₁+a_n= a₁+a₁+(n−1)*r= 2a₁+(n−1)*r

mietek: Eto, wrzuciłem to w wolfram i wtedy też n∉N₊, o co tu chodzi?

mietek: 5−latek, wynik wyjdzie ten sam.. obliczyłem też z tego wzoru no chyba, że ciągle gdzieś popełniam błąd

Eta: Czytał kilka dni z "hakiem" Chyba,że że Allel wpisała błędną liczbę stron ?

Allel: Na milion procent tak pani nam podyktowala!

5-latek : NIgdzie nie robisz bledu należy napisac . Przeczta po 12 dniach . A sam zainteresowany moglby uzyc tez swojego mózgu i policzyć sobie

Allel: To jak umie to ktos rozwiazac?

5-latek : To uczen liceum nie unie rozwiazac zwykłego równania kwadratowego ? Wstyd . I nie piszse tego żeby obrazić

Allel: jestem w 3 gimbie to po pierwsze robie zadania z nudow a chce sie tego nauczyc

Eta: Jak napisał mietek ...................... tylko zamiast 360 to 380 stron n²+4n−190=0 Δ=776 √Δ≈27,9

	−4+27,9
n=		≈ 11,9
	2

czyli przeczytał tę książkę po 12 dniach

Allel: nwm gdzie robie blad i tyle dlatego prosze o pelne rozwiazanie

Allel: mam moze glupie dla was pytanie czemu ten wzor a nie −4 −27,9itd ?

Eta: bo n>0 −−− liczba dni

Allel: jezu no tak dziekuje i to jest napewno dobrze?

Eta: Jeżeli nic nie pominęłaś w treści zadania ( to innej możliwości nie ma

5-latek : jasne

Allel: ej a teraz to glupieje xd. Wyznacz x tak aby x+2,3x−1,5x−3 w danej kolejnosci tworzyly ciag arytmetyczny. wychodzi mi sprzecznosc

5-latek : 3 gimnzajum

	x+2+5x−3
3x−1=
	2

Janek191: x ∊∅

Allel: 5 latek z tego wychodzi 0=0 wiec?...

Janek191: Naucz się liczyć 6 x − 2 = 6 x − 1 − 2 ≠ − 1

Allel: o boze...

Allel: kurde dobrze za pierwsyzm razem obliczylam i napisalem ze sprzecznosc...

Janek191: Jakiś obojniak ? obliczyłam , napisałem

5-latek : jeśli tak wychodzi to masz równanie tozsamosciowe wiec kazda liczba podstawiona za x spelnia to równanie Ale sprawdzmy to post 19:38 2(3x−1)=6x−1 6x−2=6x−1 6x−6x= −1+2 0=1 sprzeczność wiec policzone masz zle Możesz również tak sprawdzić a₂−a₁= a₃−a₂

Allel: Slownik... moj brat korzysta z komputera czesciej ode mnie

zdziwiony mietek: ?

mietek: 40466 − rozumiem do 2 = h = a, ale potem nie wiem skąd bierze się to równanie z 3 ułamkami − proszę o podpowiedź

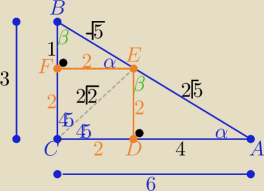
Eta: Podaję inny sposób |BC|=a=3 |DE|=|FE|=2 to |BE|=√2²+1²=√5

	2
trójkąty DAE i FEB są podobne z cechy (kkk) w skali k=		=2
	1

to: |DA|=4 i |EF|=2√5 zatem |AC|=6 i |AB|=3√5

Eta:

	√2ab		√2*3*6
Sprawdzenie : |CE|=		=		= 2√2
	a+b		3+6

mietek: Takie rozwiązanie rozumiem, dziękuje

Eta:

Krzychu: ktoś pomoże liczę zadanie i wyszło mi z wzoru herona √1056 jak to rozłożyć żeby wyszło tak jak w odpowiedzi P=84cm²

Eta: Mamy zgadywać ? .... o jakie zadanie Ci chodzi?

Krzychu: Boki trójkata maja dł.21cm,17cm,10cm OBLICZ:a)pole trójkąta,b)długośc promienia okręgu opisanego na tym trójkacie,c) długośc promienia okręgu wpisanego w ten trójkat

Eta:

	48
p=		=24
	2

P=√24*3*7*14=√7056=84

	2P
r=		=...........
	a+b+c

	abc
R=		=..........
	4P

dokończ............

5-latek : Przeciez Ty nie potrafisz liczyc i myslec czy √1056= 84 ? To jak chcesz to rozlozyc ?

Mila: wzór Herona P=√p*(p−a)*(p−b)*(p−c)

	21+17+10
p=		=24
	2

Policz jeszcze raz. Masz błąd w rachunkach.

Eta: P=√24*3*7*14=√16*9*49=4*3*7=84

5-latek : Do tego jeszcze naucz się korzytstac z tablic gdzie masz wzory

Krzychu: no tak źle połowę obwodu obliczyłem wcześniej dlatego nie mogłem wyłączyć tych 1056 r= 168/64= 3,5 R= 3570/336=10,625

Eta: No i Ci się "oberwało" Krzychu

Krzychu: wiem nie umiem podejść do zadania mając wzory w tablicach

Eta:

	168
r=		=3,5
	48

Krzychu: robię właśnie to samo tylko na innych liczbach 16,24,12 połowa obw=16+24+12/2 =26

Krzychu: wzór herona 26*10*2*14=7280

5-latek : To nie jest wzor Herona O czym zapomniales

Krzychu: 26*(26−16)*(26−24)*(26−12)=26*10*2*14 = 7280

5-latek : A pierwiastek to poszsedl sobie gdzie ? Do panienki ?

Krzychu: √7280 sry

Laura: Dane sa dwie funkcje f(x)=x2 i g(x)=1/x oblicz pole wyznaczane, przez te dwie funckje, uklad wspolrzednych dla x i prosta x=4 Czy pole to bedzie calka oznaczona 4 ∫ x2−1/x dx? 0

5-latek : No to teraz nalezaloby ten pierwiastek jakos inaczej rozpisać Możesz to zrobić w ten sposób ze 7280 rozkladaz na czynniki pierwsze potem te czynniki wstawiasz pod pierwistki i mnożysz to wszystko

Krzychu: 7280/2 3640/2 1820/2 910/2 455/5 91/91 /1

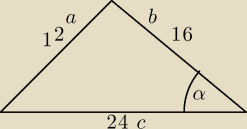
5-latek : Zaraz muszse isc spac bo jutro do pracy ale dlaczego nie liczysz np. z tw cosinisow W trojkacie naprzeciw mniejszsego boku lezy mniejszy kat (dlatego masz kat α naprzeciwko boku 12 Polle trego trojkata to P=0,5*b*c*sinα ================== Z twierdzenia cosinusow obliczysz cos α sinα= √1−cos²α podstawiasz do wzoru i gotowe

Krzychu: ok spróbuję tą metodą dobranoc

Krzychu: dziękuje za pomoc 5−latku

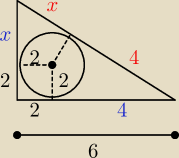
mietek: Oblicz pole trójkąta prostokątnego o jednej z przyprostokątnych długości 6 cm, jeśli promień okręgu wpisanego w ten trójkąt jest równy 2. Zrobiłem rysunek, utknąłem, przejrzałem rozwiązania z internetu i na czerwono zaznaczyłem to co wg. znalezionych rozwiązań powinno się tam znaleźć... niestety nie wiem z czego to wynika.. Nie chcę przyjmować, że tak jest, bo tak.. chciałbym to zrozumieć, bo zawsze planimetria sprawiała mi najwięcej problemów... nadeszła pora (2 mc do matury ) żeby to zmienić, więc proszę o pomoc

Ania: Pomóżcie mi bo nie umiem dodać nowego zadania oblicz resztę z dzielenia wielomianu W(x)= (x⁸ + 8x⁷ + 8 ) ³ przez wielomian Z(x) = x+8.

mietek: Nowego zadania póki co nie dodasz, bo Admin pracuje nad ulepszeniem forum. Jeżeli chcesz poznać resztę z dzielenia wielomianu w(x) przez wielomian z(x)=x−a to podstaw "a" pod "x" w w(x) Pamiętaj, że a = −8 (bo wzór to x−a, nie x+a) ( (−8)⁸ + 8*(−8)⁷ + 8 )³ = ... = 512

Mila: W(−8)=[(−8)⁸+8*(−8)⁷+8]³=(8⁸−8⁸+8)³=8³ Reszta=8³

Laura: https://matematykaszkolna.pl/forum/319456.html Prosze o pomoc

Ania: Dziękuje bardzo!

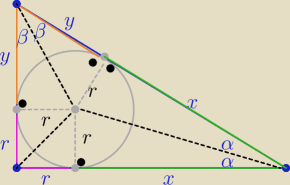
Eta: @ mietek Korzystasz z twierdzenia o odcinkach stycznych ( poczytaj o tym twierdzeniu......

Eta: I teraz z tw. Pitagorasa (2+x)²+6²=(4+x)² ⇒ ..................... x=6 to a=6 , b=2+6=8 , c= 4+6=10

df: Wyznacz wszystkie wartości parametru m, dla których równanie x²+(3−m²)+m²+m−2=0 ma dokładnie trzy rozwiązania. podstawiam za |x|=t , t≥0 t²+(3−m²)t+m²+m−2=0 no i stwierdzam ,ze 3 rozwiazania beda wtedy gdy rownanie ma dokladnie 2 rozwiazania, gdzie jednym z nich bedzie 0 a drugim liczba dodatnia z pierwszym warunkiem nie ma problemu f(0)=0 i wychodzi m=−2 lub m=2 a nie wiem jak rozgryzc, ze 2 liczba bedzie dodatnia? kombinowalem tak, ze skoro jest to liczba dodatnia ,to czyli jest to wieksza niz , więc

	−b+√Δ
		>0 , ale to nie zagralo
	2a

bardzo bym prosil o wskazowke

Laura: https://matematykaszkolna.pl/forum/319456.html Prosze o pomoc

Eta: @df napisz poprawnie dane równanie!

mietek: Obejrzałem film na ten temat (na youtube), coś do mnie dotarło dziękuje