Planimetria Lachu: Proszę o pomoc PLANIMETRIA zad 1 Długosc jednej z przyprostokątnych trójkąta prostokątnego jest równa 3. Oblicz dlugosc pozostalych boków jeśli odcinek dwusiecznej kąta prostego zawarty w trójkącie jest równy 2√2 zad 2 Podstawą trójkąta równoramiennego ABC jest odcinek AB. Na boku BC istnieje punkt D taki, że AB=AD=CD oblicz miary kątów trójkąta zad 3 W trójkąt prostokątny wpisano okrąg. Przeciwprostokątna została podzielona przez pkt stczności z okregiem na odcinki o dlugosci 2 i 3 cm Oblicz dlugosci przyprostokątnych tego trojkata oraz promien okregu wpisanego ( na tym zad zalezy mi najbardziej) Prosze o wskazówki

Lachu: pls

Godzio:

	h
sin45 =
	2√2

√2
	* 2√2 = h
2

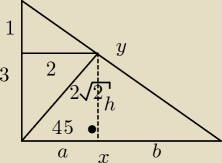
2 = h =a

3(a+b)		3 * 2		2(a+b)
	=		+		/ *2
2		2		2

3(2+b) = 6 + 2(2+b) 6 + 3b = 6 + 4 + 2b b = 4 x = a+b = 6 3² + 6² = y² 9 + 36 = y² y = 3√2

Lachu: Dzieki ale w sumie te równania sa niepotrzebne bo mozna zrobic z podobienstwa

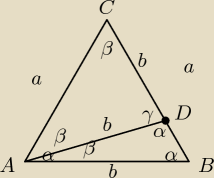
Godzio: β+2α = 180 γ + 2β = 180 γ = 180−α 180−α + 2β = 180 α = 2β β + 4β = 180 5β = 180 β = 36 α = 72

Lachu: kurde super dzieki wiem skad sie wzielo

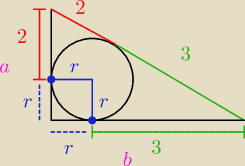
Godzio: (2+r)² + (3+r)² = 5² 4 + 4r +r² + 9 + 6r + r² = 25 2r² + 10r − 12 = 0 /:2 r² + 5r − 6 = 0 r² − r + 6r − 6 = 0 r(r−1) + 6(r−1) =0 (r−1)(r+6) = 0 r = 1 v r = −6 − odrzucamy bo r > 0 r=1 a = 2+r = 3 b = 3+r = 4

Godzio:

Lachu: o kurde ze na to nie wpadlem, super dzieki wielkie...