calka nieoznaczona
Laura: ∫(3x2+2x)lnx dx
Obliczylam metoda przez czesci
i wyszlo mi (x3+x2)*lnx− (1/2x2+1/3x3) + C
lub prosciej (x3+x2)*lnx− 1/2x2−1/3x3 + C
Czy dobrze?
11 mar 10:58
Benny: Policz pochodną wyniku
11 mar 11:08
Jerzy:
Jest drobny błąd...∫2dx = 2x
11 mar 11:18
Jerzy:
Więcej...cały drugi człon jest zły
11 mar 11:21
Laura: ∫(3x2+2x)lnx dx = (x3+x2)*lnx− ∫1/x* x(x+x2)dx=(x3+x2)*lnx−x2/2+x3/3
Gdzie popelnilam blad?
11 mar 12:47
Jerzy:
| | 3x2 + 2x | |
..−∫ |
| dx = − ∫(3x +2)dx |
| | x | |
11 mar 12:52
Laura: Tragedia. Nigdy w życiu tego nie zalicze. Dzięki za pomoc
11 mar 15:59
Laura: Pisze tutaj bo nie da sie dodac nic nowego. Dane sa dwie funkcje f(x)=x2 i g(x)=1/x oblicz
pole wyznaczane, przez te dwie funckje, uklad wspolrzednych dla x i prosta x=4
13 mar 21:10
Laura: dla x>0
13 mar 21:11
Laura: Wykres tego pola obraca sie 360 stopni wzgledem x−aksen i tworzy bryle o danej objetosci.
Oblicz objetosc i to samo wzgledem y−aksen'
13 mar 21:14
Laura: Oblicz calki bez uzycia wzorow:
oznaczone:
e
∫ (3−x
2)/x dx
1
nieoznaczone:
∫x*
√3−x2 dx
∫x*
√3−x dx
∫x
2 * cos( x
3 ) dx
| | x*sin (x2) | |
∫ |
| |
| | 2 + cos (x2) | |
13 mar 21:23
Laura: Wyznacz t w calce oznaczonej w danym rownaniu:
t
∫(2e(2x) −3 ex)dx = 0
0
13 mar 21:25
Laura: Pole jest wyznaczane przez dwie funkcje f(x)=−x3 + 3x2 + 2 i g(x)= x2+ 2 Wyznacz pole przy
pomocy pochodnej i wyznacz objetosc bryly powstalej przez obrocenie powstalej figury o 360
stopni wzgledem y aksenu.
Inne pole jest wyznaczane przez wykres g(x)= x2+2 oraz x−aksen oraz dwie linie x=0 i x=2.
Wyznacz objetosc bryly powstalej poprzez obrocenie wyznaczonej figury o 360 stopni wzgledem
x−aksenu
13 mar 21:32
Laura: Pomoglby mi ktos?
13 mar 21:32
Mila:
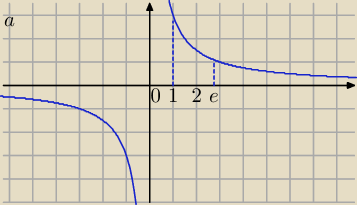
1)
| | 3−x2 | | 3 | |
1∫e |
| dx=1∫e( |
| )dx−1∫exdx |
| | x | | x | |
| | 3 | |
a) 1∫e( |
| )dx=[lnx]1e=3*(lne−ln1)=3*(1−0)=3 |
| | x | |
| | 1 | | 1 | |
b) 1∫ex dx=[ |
| x2]1e= |
| (e2−1) |
| | 2 | | 2 | |
| | 3−x2 | | 1 | | 1 | | 7 | | 1 | |
1∫e |
| dx=3− |
| e2+ |
| = |
| − |
| e2 |
| | x | | 2 | | 2 | | 2 | | 2 | |
13 mar 21:36
Mila:
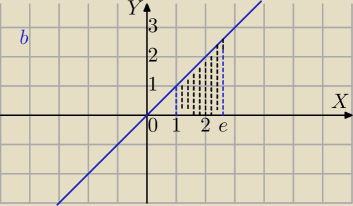
13 mar 21:42
Mila:
2)
∫x*
√3−x2 dx=..
| | −dt | |
[3−x2=t −2xdx=dt, xdx= |
| ] |
| | 2 | |
| | 1 | | 2 | | −1 | |
dt=− |
| * |
| t32= |
| *(3−x2)23= |
| | 2 | | 3 | | 3 | |
13 mar 21:49
Mila:
3)
∫x*
√3−x dx=..
[3−x=t, −dx=dt, x=3−t]
..=−∫(3−t)*
√t dt=−∫(3t
12−t
32) dt=
| | 2 | | 2 | |
=∫(t32−3t12)dt= |
| t52−3* |
| *t32= |
| | 5 | | 3 | |
wróć do podstawienia i dokończ.
13 mar 21:57
Laura: Wow dzieki

13 mar 21:58
Laura: Dane sa dwie funkcje f(x)=x2 i g(x)=1/x oblicz
pole wyznaczane, przez te dwie funckje, uklad wspolrzednych dla x i prosta x=4
Czy pole to bedzie calka oznaczona
4
∫ x2−1/x dx?
0
13 mar 22:06
Mila:
Napisz dokładnie treść zadania.
13 mar 22:09
asd: Pytanie nie z tematu: Czy macie problemy z dodaniem zadania?
13 mar 22:28
Mila:
Nie.
13 mar 22:33
Mila:
Tak.
Dopisz swoje zadanie do istniejącego postu.
13 mar 22:34
asd: Trójkąt ABC ma boki długości a,b,c, a trójką DEF ma boki długości 2a,2b,2c. Wynika stąd że:
A. PABC=4 PDEF
B. PABC=2 PDEF
C. PABC= 12 PDEF
D. PABC= 14 PDEF
13 mar 22:49
Laura: To jest cale zadanie. Nie ma nic wiecej.
13 mar 22:49
Laura: Mila, a jak rozwiazac to 2/5(3−x)
(5/2)−2(3−x)
(3/2)

13 mar 22:53
Mila:
Trójkąt DEF jest dwa razy większy, to jego pole jest 4 razy większe od pola ΔABC.
ΔABC jest dwa razy mniejszy od ΔDEF.
Pole ΔABC jest 4 razy mniejsze od pola ΔDEF.
wybierz odpowiedź.
13 mar 22:53
asd: D?
13 mar 23:03
Mila:
Możesz zostawić taki wynik 22:53
Lepiej jednak doprowadzić do najprostszej postaci
3−x≥0
| | 2 | |
= |
| *(3−x)2*√3−x−2*(3−x)*√3−x= |
| | 5 | |
| | 2 | |
=(3−x)*√3−x*( |
| *(3−x)−2) możesz jeszcze wykonać w nawiasie. |
| | 5 | |
x
23=
3√x2
x
32=
√x3=x
√x, x≥0
a
34=
4√a3
Potęgi sobie przypomnij.
13 mar 23:03
Mila:
asd, dobrze.
13 mar 23:04
Laura: Dane sa dwie funkcje f(x)=x2 i g(x)=1/x oblicz
pole wyznaczane, przez te dwie funckje, uklad wspolrzednych dla x i prosta x=4
Czy pole to bedzie calka oznaczona
4
∫ x2−1/x dx?
0
Wie ktos moze?
13 mar 23:21
13 mar 23:22
Mila:
Nie wpisuj tyle razy tego samego zadania?
13 mar 23:22
Laura: Oblicz calki:
∫x2 * cos( x3 ) dx
13 mar 23:30
tss: / 2+cos(x
2)=u
| | 1 | | du | | 1 | |
=− |
| ∫ |
| =− |
| ln|u|+C= |
| | 2 | | u | | 2 | |
/ u>0 dla x∊R /
| | 1 | | 1 | |
=− |
| ln(u)+C=− |
| ln(2+cos(x2))+C |
| | 2 | | 2 | |
14 mar 00:01
tss: ∫x
2*cos(x
3)=
/u=sin(x
3)
du=3x
2cos(x
3)
| | 1 | | 1 | | 1 | |
= |
| ∫du= |
| u+C= |
| sin(x3)+C |
| | 3 | | 3 | | 3 | |
14 mar 00:08
Laura: dziekuje!
14 mar 00:13
Laura: Dane sa dwie funkcje f(x)=x2 i g(x)=1/x oblicz
pole wyznaczane, przez te dwie funckje, uklad wspolrzednych dla x i prosta x=4
13 mar 21:10
Laura: dla x>0
13 mar 21:11
Laura: Wykres tego pola obraca sie 360 stopni wzgledem x−aksen i tworzy bryle o danej
objetosci.
Oblicz objetosc i to samo wzgledem y−aksen'
14 mar 00:21
Laura: policz calke
∫(−x3+3x2+2)−(x2+2) dx
14 mar 00:23
Laura: ∫x2 * cos( x3 ) dx
14 mar 00:39
Laura: calka ∫2e2x − 3ex dx pomocy
14 mar 00:57
Jerzy:
1) rozbij na całki elementarne
2) przez części v' = cos3x
3) = 2e2∫x −3∫ex = e2x2 − 3ex + C
14 mar 09:14
Jerzy:
Pole = ∫x2dx + ∫1/xdx ....pierwsza w granicach <0,1> druga <1,4>
14 mar 09:19
Mariusz:
∫x
2cos(x
3)dx
t=x
3
dt=3x
2dx
| | 2 | | 2 | |
∫2xcos(3x)dx= |
| xsin(3x)− |
| ∫sin(3x)dx |
| | 3 | | 3 | |
| | 2 | | 2 | |
∫2xcos(3x)dx= |
| xsin(3x)+ |
| cos(3x)+C |
| | 3 | | 9 | |
14 mar 10:23
Laura: Dzięki !
14 mar 11:28
Laura: Dziekuje wszystkim za pomoc. Za tydzien mam korepetycje z matematyki... Zobaczymy czy mi sie da
jeszcze pomoc...
14 mar 12:59
 1)
1)


