Równania okręgu i tak dalej..
Kaarolina: Wyznacz równanie stycznej do okręgu o jakimś podanym równaniu ,która (ta styczna) jest
prostopadła do jakiejś prostej ?
Bazuje na zadaniu z matury rozszerzonej listopad 2015 , gdzie treść zadania brzmi :
Wyznacz równanie stycznej do okręgu o równaniu x
2 −6 x+ y
2 +10 y=0 prostopadłej do prostej
3x−4y+5=0
Przeglądam różne opracowania rozwiązania i nie wiem DLACZEGO nagle z 3x−4y+5=0 wyszło 4x+3x ...
? Bo dalej wiem dlaczego C=0 i co dalej jeśli już miałabym zrobić przy takiego typu zadaniu
Ktoś by był w stanie wytłumaczyć mi to po ludzku ?
Z góry dzięki
17 lut 18:07
Kaarolina: Poprawa :
DLACZEGO nagle z 3x−4y+5=0 wyszło 4x+3y ...
Ktoś coś ?
17 lut 18:08
5-latek: Dlatego ze prosta prostopadla do prostej Ax+By+C=0 ma równanie Bx−Ay+D=0
17 lut 18:22
Ania: No dobrze, wiem , zauważyłam ale dlaczego ? Skąd to się bierze?
17 lut 18:26
17 lut 18:32
5-latek:
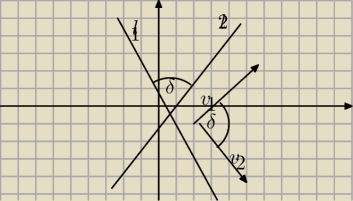
l
1 A
1x+B
1y+C
1=0
l
2 A
2x+B
2y+C
2=0
gdzie A
12+B
12>0 i A
22+B
22>0
Aby obliczyć kąt miedzy tymi prostymi l
1 i l
2
Wezmy dwa wektory v
1[A
1 B
1] i v
2{A
2,B
2]
Wektory te sa odpowiednio prostopadle do prostych l
1 i l
2
Niech teraz ∡(v
1,v
2)=δ wtedy mamy 0≤δ≤π
Na podstawie kata miedzy wektorami mamy wzory
| | A1*A2+B1*B2 | |
cosδ= |
| |
| | √A12+B12*√A22+B22 | |
| | |A1B2−A2B1 | |
oraz sinδ= |
| } |
| | √A12+B22*√A22+B22 | |
Ponieważ wektory sa prostopadle do prostych a wiec kat δ musi być rowny jednemu z katow
utworzonych przez proste l
1 i l
2 (oznaczny go również przez δ
Wiec dwa ostatnie wzory możemy zastosować do obliczenia kąta miedzy prostymi
Teraz ze wzoru cosδ=0 otzrymamy warunek prostopadlosci prostych l
1 i l
2
A
1A
2+B
1*B
2=0
========================
a zze wzoru na sinδ= 0
mamy związek A
1B
2−A
2B
1=0
================================
który stwierdza ze dane proste sa rownolegle lub się pokrywają
17 lut 19:00