Przygotowanie do matury #29
The City:
Rozwiąz równanie |x2 + 4x − 5| + |x2 + 4x| = 5
To co dla mnie jest tu nowe to obecność równań kwadratowych w wartościach bezwzględnych.
Gdyby było, np. |x−5| + |x+4| = 5 to wyznaczyłbym przedział itd.., a tutaj nie wiem co robić −
też jakieś przedział? Jeśli tak to jakie? Od miejsc zerowych obu funkcji?
16 lut 18:34
16 lut 18:41
The City:
o jak miło, nawet nie wiedziałem, że taka strona jest
dziękuje
16 lut 18:42
prosta:
można przyjąć: x2+4x=t
|t−5|+|t|=5
16 lut 18:46
5-latek: Masz po lewo cala nawigacje
16 lut 18:46
16 lut 18:47
The City:
Policzę to potem podstawiając zmienną pomocniczą, ale chciałbym znać "tradycyjny" sposób.
Czy skoro dla równania kwadratowego będę wyliczał przedziały w których są argumenty zwracające
wartości nieujemne i ujemne, to czy jak będę miał 2 takie nierówności (jak w tym zadaniu,
które podałem w 1 poście) to będę wyznaczał części wspólne dla ujemnych i nieujemnych z obu
nierówności kwadaratowych?
16 lut 18:51
prosta:
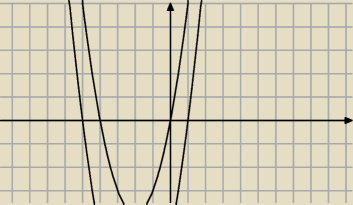
miejsca zerowe wyznaczą przedziały na osi liczbowej dla których
funkcje zwracają wartości dodatnie oraz ujemne
mamy przypadki: (−
∞,−5)∪(1,+
∞)
<−5,−4>∪<0,1>
(−4,0)
16 lut 19:35
prosta:
pracochłonne....
16 lut 19:37
16 lut 19:51
Metis: Nie mogę znaleźć postu
Ety z rozwiązaniem podobnego zadanka
a pamiętam, że fajnie tam
było wszystko narysowane
16 lut 20:10
The City:
Dzięki za cynk
, może kiedyś na to natrafię, ale póki co lecę z kolejnymi zadaniami.
16 lut 20:25