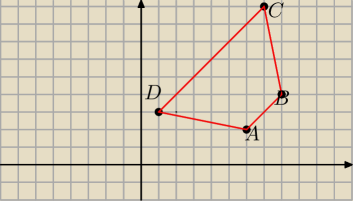
 Do a)
Sprawdz czy |AD|=|BC| (wzor na dlugosc odcinka i AB||CD
jeśli nie to na tym trapezie nie można opisac okręgu
jeśli tak to można przystapic do podpunktu b)
Czyli
1. Napisac równanie symetralnej boku AB
2. Napisac równanie symetralnej boku BC
Punkt przecięcia tych symetralnych to srodek okręgu opisanego na tym trapezie
3. Odlegosc srodka okręgu opisanego na tym trapezie od np. wierzchołka A to promien okręgu
opisanego na tym trapezie
Wiec działaj
Do a)
Sprawdz czy |AD|=|BC| (wzor na dlugosc odcinka i AB||CD
jeśli nie to na tym trapezie nie można opisac okręgu
jeśli tak to można przystapic do podpunktu b)
Czyli
1. Napisac równanie symetralnej boku AB
2. Napisac równanie symetralnej boku BC
Punkt przecięcia tych symetralnych to srodek okręgu opisanego na tym trapezie
3. Odlegosc srodka okręgu opisanego na tym trapezie od np. wierzchołka A to promien okręgu
opisanego na tym trapezie
Wiec działaj
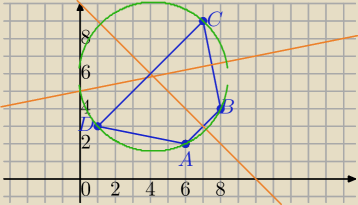 a)
AB→=[2,2]
DC→=[6,6]
AB||DC
wykaż, że |AD|=|BC|
b) symetralna AB− zbiór wszystkich punktów jednakowo odległych od końców odcinka.
A=(6, 2), B=(8, 4)
(x−6)2+(y−2)2=(x−8)2+(y−4)2⇔
y=−x+10
symetralna BC:
B=(8, 4),C=(7, 9)
(x−8)2+(y−4)2=(x−7)2+(y−9)2⇔
a)
AB→=[2,2]
DC→=[6,6]
AB||DC
wykaż, że |AD|=|BC|
b) symetralna AB− zbiór wszystkich punktów jednakowo odległych od końców odcinka.
A=(6, 2), B=(8, 4)
(x−6)2+(y−2)2=(x−8)2+(y−4)2⇔
y=−x+10
symetralna BC:
B=(8, 4),C=(7, 9)
(x−8)2+(y−4)2=(x−7)2+(y−9)2⇔
| 1 | ||
y= | x+5 | |
| 5 |
| 1 | ||
−x+10= | x+5 | |
| 5 |
| 25 | 35 | |||
x= | , y= | |||
| 6 | 6 |
| 25 | 35 | |||
S=( | , | ) | ||
| 6 | 6 |
| 25 | 35 | |||
r2=|SD|2=(1− | )2+(3− | )2 | ||
| 6 | 6 |
| 325 | ||
r2= | ||
| 18 |
| 25 | 35 | 325 | ||||
(x− | )2+(y− | )2= | ||||
| 6 | 6 | 18 |