Udowodnij Agata: Dane są cztery punkty leżące na płaszczyźnie A(6, 2) , B(8,4) , C( 7,9) oraz D( 1,3) Udowodnij, że czworokąt ABCD jest trapezem równoramiennym. Z góry dzięki!

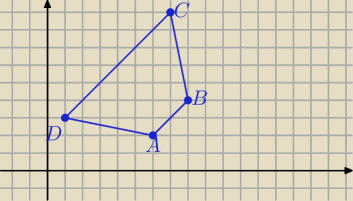
Janek191: Sprawdź, że pr AB II pr CD ( oblicz współczynniki kierunkowe) Oblicz długości odcinków : BC i AD.

Agata: |BC| = [ −1; 5] |AD| = [−5; 1] Ale jak mam to udowodnic?

Basia: skoro znasz wektory to policz wspolzedne CD^→ i AB^→ i pokaz, ze AB^→= α*CD^→ z tego wynika, ze wektory sa rownolegle albo policz |AB^→,CD^→| = u₁*w₂−u₂*w₁ dostaniesz 0 (czyli sin(<AB^→.CD^→)=0) czyli AB^→|| CD^→ albo policz wspolczynniki kierunkowe prostych AB i CD |BC|=√1+25=√26 |AD|=√25+1 = √26

Agata: Może ktoś pomoc mi w całosci?

jc: Wystarczy pokazać, że prosta przechodząca przez środki podstaw jest osią symetrii czworokąta. P=(1/2)(A+B)=(7,3) Q=(1/2)(C+D)=(4,6) v=P−Q=(3,−3) || (1,−1) kierunek prostej v*(B−A)=(1,−1)*(2,2)=0, prosta jest prostopadła do pierwszej podstawy v*(C−D)=(1,−1)*(6,6)=0, prosta jest prostopadła do drugiej podstawy czyli faktycznie prosta jest osią symetrii czworokąta.

Janek191:

	4 − 2
a1 =		= 1 − współczynnik kierunkowy pr AB
	8 − 6

	3 − 9
a2 =		= 1 − współczynnik kierunkowy pr CD
	1 − 7

a₁ = a₂ więc te proste są równoległe ( odcinki AB i CD są podstawami trapezu) → BC = { 7 −8, 9 − 4] = [ − 1, 5] I BC I = √(−1)² + 5² = √26 oraz → AD = [ 1 − 6, 3 − 2] = [ − 5, 1] I AD I = √26 więc boki BC i AD są równe, czyli czworokąt ABCD jest trapezem równoramiennym.