Geometria analityczna Amelia : Dane są cztery punkty leżące na płaszczyźnie: A(6, 2), B(8, 4), C(7, 9) oraz D(1, 3). b) Napisz równanie okręgu opisanego na tym trapezie.

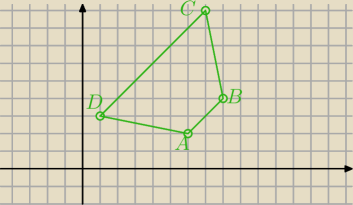
Tadeusz: Mozna to rozwiązać na "szamanaście" sposobów np rozwiązując układ równań (później sprawdzić czy czwarty punkt nalezy do okręgu) (6−x_s)²+(2−y_s)²=r² (8−x_s)²+(4−y_s)²=r² (7−x_s)²+(9−y_s)²=r²

a7: w linku rozwiązanie Mili https://matematykaszkolna.pl/forum/370169.html

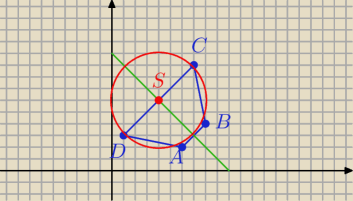
janek191: y = 10 − x S = ( x, 10 − x) C = ( 7, 9) B = ( 8, 4) I SCI² = I SB I² ( 7 − x)² + ( 9 − 10 + x)² = ( 8 − x)² + ( 4 − 10 + x)² 49 − 14 x + x² + x² −2 x + 1 = 64 − 16 x + x² + x² − 12 x + 36 50 − 16 x = 100 − 28 x 12 x = 50

	1
x = 4
	6

	5
y = 5
	6

oraz

	325
r2 =
	18

	25		35		325
Odp. ( x −		)2 + ( y −		)2 =
	6		6		18

Tadeusz: albo: skoro na trapezie opisać można okrąg to musi to być trapez równoramienny. Środek okręgu musi leżeć na osi symetrii. Potrafisz napisać jej równanie y=−x+10 Szukasz na tej prostej punktu równoodległego od wierzchołków itd

dero2005:

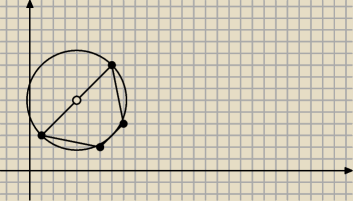
	25		35		650
(x−		)2+(y−		)2=
	6		6		36

janek191: Ale wysyp rozwiązań

a7: no własnie dawno tak nie było