Geometria Klaudia: Dane są cztery punkty leżące na płaszczyźnie: A(6, 2), B(8, 4), C(7, 9) oraz D(1, 3). b) Napisz równanie okręgu opisanego na tym trapezie. Jak zrobić ten podpunkt ? Proszę o wskazówki

jc: Skąd bierzesz taką irytującą notację: A(6,2)? Potem jest kłopot z rachunkami, bo czy można napisać A−B? czy racze A(6,2)−B(8,4)?

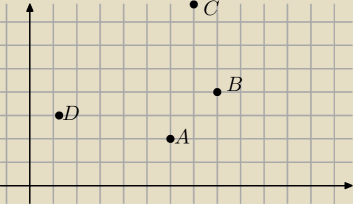
Basia: jest kilka spsobow 1) S(a,b) rownanie okregu (x−a)²+(y−b)²=r² trzy niewiadome czyli podstawiamy wspolrzedne trzech punktow i rozwiazujemy uklad trzech rownan 2) S jest punktem przeciecia symetralnych bokow bierzemy dwa nie rownolegle boki np. AB i BC piszemy rownania symetralnych rozwiazujemy uklad dwoch rownan i mamy wspolrzedne S r = AS (lub BS lub CS lub DS) zakladam, ze na tym trapezie da sie opisac okrag (bo nie sprawdzalam) musi byc rownoramienny C nie jest zaznaczony poprawnie, 9 sie nie zmiescilo

Klaudia: Mógłby ktoś spojrzeć na moje rozw., coś mi chyba nie wyszło Proszę https://www.dropbox.com/s/2kwc886cm4q0kmy/20180225_192925.jpg?dl=0

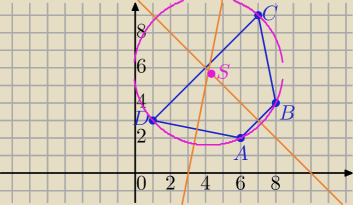Mila: A(6, 2), B(8, 4), C(7, 9) oraz D(1, 3). 1) Trapez jest równoramienny, można na nim opisać okrąg. Środek okręgu opisanego na wielokącie wypukłym leży w punkcie przecięcia symetralnych boków . 2) symetralna AB: (x−6)²+(y−2)²=(x−8)²+(y−4)²⇔y=−x+10 Symetralna AD: (x−6)²+(y−2)²=(x−1)²+(y−3)² ⇔y=5x−15 −x+10=5x−15 6x=25

	25		35
x=		i y=
	6		6

	25		35
3) S=(		,		)
	6		6

4) promień

	25
|AS|2=(		−6)2+(U{35}{6−2)2
	6

|AS|²=(11/6)²+(23/6)²=325/18

	325
R2=
	18

5) Równanie okręgu:

	25		35		325
(x−		)2+(y−		)2=
	6		6		18

=======================