planimetria
Eta: Zadania z "ukochanej "
 planimetrii
planimetrii dla
Jack
zad1/
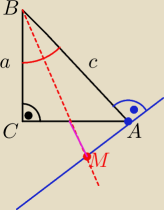
W trójkącie prostokątnym ABC o przyprostokątnej |BC|=a i przeciwprostokątnej |AB|=c
poprowadzono dwusieczną kąta B .która przecięła w punkcie M prostą prostopadłą do AB
i przechodzącą przez punkt A.
Wykaż , że odległość punktu M od prostej AC jest równa
c−a
zad2/
W wycinek koła o kącie środkowym 60
o wpisano okrąg o środku w punkcie O i promieniu R
Następnie wykreślono okrąg ośrodku S i promieniu r styczny zewnętrznie do pierwszego okręgu
i jednocześnie styczny do ramion kąta tego wycinka.
Wykaż ,że
R=3r
1 sty 17:41
5-latek: Witam w Nowym roku

Pozdrawaim
A co zrobisz jak za dwa miesiące
Jack napisze do Ciebie ze kocha planimetrię ?
1 sty 17:46
Jack: między miłością a nienawiścią jest bardzo cienka granica...
1 sty 18:11
Jack: a tak wgl teraz jestem zajety...

ucze sie metody eliminacji Gaussa
1 sty 18:11
Metis:
1)

1 sty 18:43
Jack:
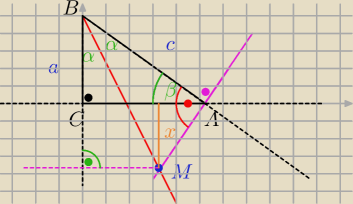
rysunek mam

1 sty 18:49
Jack: x = 2 sin
2 α * c
tylko od "a" bym teraz musial jakos...

1 sty 18:53
Eta:
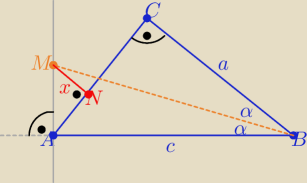
Proponuję taki rys.
1 sty 18:53
Jack: sadze ze moj jest lepsz... ; D
1 sty 18:54
Metis: Z trójkąta ABM wyliczyć AM z tw cosinusów.
Potrzebny jeszcze AN i jesteśmy w domu.
1 sty 18:56
Eta:
No i ładnie
Jacuś
| | a | |
teraz : |
| = cos(2α) ⇒ .......... i 2sin2α= 1−cos(2α) |
| | c | |
i..................................... mamy tezę

1 sty 18:57
Jack: @Metis
sadze ze tym tw. cosin. to raczej na okolo zupelnie...i jak co to odleglosc prostej od punktu
jest zawsze pod katem prstym
1 sty 18:57
Eta:
Twoje wszystko jest "lepsze"! nawet jeśli nie jest .......

1 sty 18:58
Metis: Więc
Eta, dobrze piszę?

1 sty 18:59
Jack: Eta
a faktycznie.... że ja tego nie zauważyłem...ehh
x = 2 sin
2 α * c
a = c* cos 2 α = c* (1 − 2 sin
2α)
c.n.u.
1 sty 19:04
Jack: nie wszystko...tylko ten rysunek ; P
1 sty 19:04
Jack:
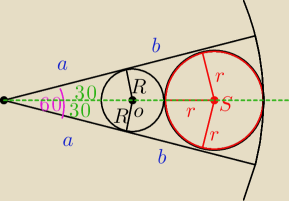
zad 2....nielogiczne zupelnie : D
Wykreślono to to samo co narysowano?
tak to ma wygladac?
1 sty 19:30
Jack:
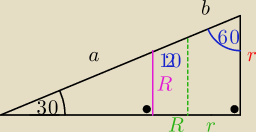
Wiem, że
a =
√3 * R
a+b =
√3 * r
i teraz...hmm
1 sty 19:47
Jack: na tym drugim rysunku dokladnie odwrotnie zaznaczylem a,b z R'kami... ehh
1 sty 19:50
pytajnik123: Jack jak doszedłeś do tego, że x = 2 sin2 α * c?
1 sty 19:58
Eta:
@
Jack
Więcej już ode mnie pomocy nie otrzymasz .....

1 sty 20:07
Jack:
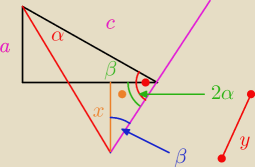
@pytajnik
2 α + β = 90, więc
90 − β = 2α
czyli
ten kąt (ten zielony) wynosi 2α
skoro tak, a tamten jest trojkatem prostokatnym to ten trzeci kąt jest 90 − 2α czyli tak
wlasciwie β
więc
sin 2 α = x do jakiejś niewiadomej...oznaczylem ja jako
y
stąd
x =
y * sin 2α
| | y | |
Nastepnie z trojkata o bokach "c, y, dwusieczna" tg α = |
| , więc y = c*tg α |
| | c | |
Podstawiąc
| | sin α | |
x = c*tg α * sin 2α = c* |
| * 2 sinα cosα = c* 2 sin2α |
| | cos α | |
1 sty 20:14
Jack: @Eta... no trudno, tego zadania i tak nie rozwiaze

]
baju baj
1 sty 20:14
Metis: Eta 18:59

1 sty 20:30
pytajnik123: Dziękuję ^^ Dobrze wytłumaczone

1 sty 20:31
Jack: :(
1 sty 21:46
Archeolog: @Jack jak R = 3r to koło z promieniem r będzie malutkie, a te z R będzie tym dużym.
(chyba to sam zauważyłeś ale wspomnę i tak)
Żeby stosunek R do r wyliczyć zrób pewien układzik równań

( S1 − środek pierwszego koła, S2− środek drugiego koła |S1S2| = r+R)
Troszkę podobne do tego zadania o które ja właśnie pytam tylko bez tej części o ciągach.
https://matematykaszkolna.pl/forum/310970.html
1 sty 22:04
Jack:
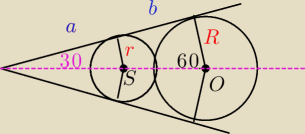
Rozpatrujac nieskonczony ciag kol
| | R | |
sin 30 = |
| |
| | R + 2r + 2r2 + ...+ 2rn | |
2R = R + 2r + 2r
2 + ...+ 2r
n
2R = 2(R + r + r
2+...+r
n) − R
| | R | |
R = R + r + r2+...+rn − |
| |
| | 2 | |
| | a1 | |
Korzystajac ze wzory na nieskonczony ciag S = |
| |
| | 1−q | |
W takim razie skoro pierwszy jest R
Czyli R = 3r
c.n.u.
1 sty 22:52
Archeolog:
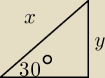
R − promień większego koła
r − mniejszego koła
x = r+R
y = R−r sin 30 = 1/2 = (R−r)/x
x = r+R
x = 2R − 2r
r+R = 2R −2r
R = 3r
c.n.u.
1 sty 23:13
Jack: @Archeolog...nie widze tego ; d
1 sty 23:16
Eta:
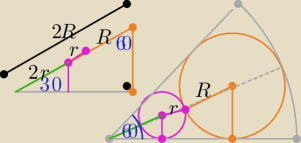
Czytanie ze zrozumieniem:
okrąg wpisany w wycinek koła o kącie środkowym 60
o
2R= 2r+r+R ⇒ R=3r
1 sty 23:28
Eta:
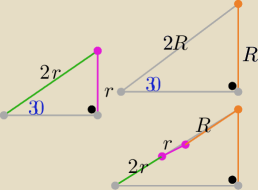
1 sty 23:34
Archeolog:
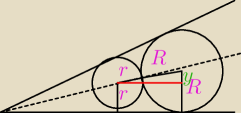
Rysunek trochę nie tak proporcjonalnie ale dane tak samo. Ten trójkąt jest podobny do tego z
kątem 30 stopni, więc ma też kąt 30 stopni.
1 sty 23:35
Jack: @Eta...a skad my wiemy ze do pierwszego okregu jest akurat 2r ?
1 sty 23:44
Eta:
Z własności trójkąta "ekierki" o kątach 30o,60o, 90o
1 sty 23:47
Jack: łe kurcze...faktycznie, ale ja głupi...
Dzieki wielkie...
1 sty 23:48
Eta:

1 sty 23:49
Jack: i dlatego nie lubie planimetrii...zawsze czegos nie zauwaze i licze na okolo
co do rozwiazania Archelogo'a to powiedzialbym ze lekko naciagane... : D
aczkolwiek pewnie jak bys uzasadnil ze sa podobne i inne takie to by bylo ok...
1 sty 23:51
Archeolog: trójkąt "ekierka" czyli trygonometria dla gimnazjum xP
1 sty 23:51
Jack: a pan Archeolog ? która klasa? : D
ide chyba zrobic cos porzadnego i poloze sie spac...
1 sty 23:54
Archeolog: pan Archeolog klasa 4 i ambitnie postanowił się całego materiału w rok szkolny nauczyć, bo
nie zauważył że to co robi się w szkole to jest mniej niż minimum.
Póki co mamy 1 stycznia i powinienem zbiory A. Kiełbasy do końca kwietnia przerobić.
1 sty 23:57
Jack: technikum ?
1 sty 23:58
Jack: prawda o tym minimum...masakra...a niektorzy maja problem ze zdaniem matury z matmy
podstawowej...
Tylko ja mam jakieś zbiory z nowej ery tandetne ? : D
1 sty 23:59
Archeolog: Czwartej klasy liceum z tego co wiem już nie ma

1 sty 23:59
Jacek: podstawowka jeszcze jest

2 sty 00:00
Archeolog: Ja miałem na samym początku roku 'test diagnostyczny' aka. próbną maturę i wyszło mi "całe" 40%
z
matmy. Wtedy miałem tylko pierwszy dział powtórzony i załamałem się tym wynikiem z podstawy.
Ostatnio pisałem gdzieś w listopadzie i wtedy miałem już funkcje itd. powtórzone i 94% z
próbnej, ale
rozszerzenie tylko 36%, bo co przerobiłem to umiałem, a umiałem 4 zadania na 11
(ze starej podstawyta próbna była).
Myślałem, że trygonometria będzie kosmosem, a okazała się nawet przyjemna
(szczególnie maturalne), ale planimetria to jest kosmos jak zaczynałem ten dział to nie umiałem
zadań z podstawowej w 5 minut zrobić, bo nic tych trójkątów podobnych nie widziałem.
2 sty 00:04
Archeolog: Jacek jakbym pisał maturę w czwartej podstawówki to raczej bym się nie obwiniał za to, że tak w
tyle
z materiałem jestem

2 sty 00:05
Jack: ja ponoc w przyszlym tygodniu mam miec probna z matmy...chetnie zobacze na co mnie stac...
tylko zamiast niektorych zadan z planimetrii bym wolal liczyc wyznaczniki macierzy, calki
nieoznaczone albo chociaz ekstrema funkcji dwoch zmiennych...czasami to jest duzo prostsze do
policzenia niz jakies zadanie z trojkatami...
2 sty 00:07
Archeolog: Ja bym ci Jack wysłał jakiś kontakt do mnie żeby dzielić się informacjami maturalnymi
(jak liczę to zazwyczaj staram się nie wchodzić na fora, nawet matematyczne bo rozpraszają), a
tutaj
nie ma prywatnych wiadomości więc tymczasowy czat postawiłem
http://tinychat.com/obmhoe .
Wbij i tam ewentualnie mogę ci podać jakieś skype albo coś.
2 sty 00:25
Jack: Na telefoniw tego nie odpale niestety ale jesli masz gg − gadu gadu to pisz śmiało 37209167
2 sty 00:26
Jack: Ewentualnie team speak 3 ale.to by ktos.musiał serwer trzymac
2 sty 00:27
Archeolog: gg może być
2 sty 00:30
Kacper:
Biorę

2 sty 08:23
5-latek: Kacper
No to jeszcze St Kartasinski i M Okolowicz
Zbior zadań maturalnych i egzaminacyjnych Cz2 Geometria i trygonometria .
Jest to jedna czesc z 7 .
Lev Kurlyandchik
Kącik olimpijski cz1 Geometria (Wydawnictwo Aksjomat )
2 sty 08:53
Kacper:
5−latek Kurlandchik−a chyba mam, a Okołowicza poszukam w bibliotece

2 sty 09:45
5-latek: 
Zobacz jeszcze do Antonow Sankin Zbior zadań z matematyki elelmentarnej
Tam tez jest dużo zadań z planimetrii .
jest tez ksiazka Waldemar Pompe W okol obrotow przewodnik po geometrii elementarnej
Kupilem ja za 12 zl (wydawnictwo szkolne Omega 2014r . Stron 48 ale wiedza kosztuje

2 sty 09:50
5-latek: W sumie nie wiem po co mi to potrzebne

2 sty 09:52
Jack:
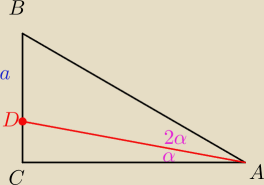
| | a(1−4sin2α) | |
wykaż że |AD| = |
| |
| | 2sinα | |
15 sty 22:53
Jack: podpowiedzi jakies? : D
15 sty 23:00
15 sty 23:16
Jack: dzieki

15 sty 23:26
Kacper:
biorę

16 sty 09:49
Jack: zad 15
Prosta o równaniu y=x(a−3) + a+ 4 ...
16 sty 19:16
 planimetrii dla Jack
zad1/
W trójkącie prostokątnym ABC o przyprostokątnej |BC|=a i przeciwprostokątnej |AB|=c
poprowadzono dwusieczną kąta B .która przecięła w punkcie M prostą prostopadłą do AB
i przechodzącą przez punkt A.
Wykaż , że odległość punktu M od prostej AC jest równa c−a
zad2/
W wycinek koła o kącie środkowym 60o wpisano okrąg o środku w punkcie O i promieniu R
Następnie wykreślono okrąg ośrodku S i promieniu r styczny zewnętrznie do pierwszego okręgu
i jednocześnie styczny do ramion kąta tego wycinka.
Wykaż ,że R=3r
planimetrii dla Jack
zad1/
W trójkącie prostokątnym ABC o przyprostokątnej |BC|=a i przeciwprostokątnej |AB|=c
poprowadzono dwusieczną kąta B .która przecięła w punkcie M prostą prostopadłą do AB
i przechodzącą przez punkt A.
Wykaż , że odległość punktu M od prostej AC jest równa c−a
zad2/
W wycinek koła o kącie środkowym 60o wpisano okrąg o środku w punkcie O i promieniu R
Następnie wykreślono okrąg ośrodku S i promieniu r styczny zewnętrznie do pierwszego okręgu
i jednocześnie styczny do ramion kąta tego wycinka.
Wykaż ,że R=3r
 Pozdrawaim
A co zrobisz jak za dwa miesiące Jack napisze do Ciebie ze kocha planimetrię ?
Pozdrawaim
A co zrobisz jak za dwa miesiące Jack napisze do Ciebie ze kocha planimetrię ?
 ucze sie metody eliminacji Gaussa
ucze sie metody eliminacji Gaussa
 1)
1) 
 rysunek mam
rysunek mam 

 Proponuję taki rys.
Proponuję taki rys.



 zad 2....nielogiczne zupelnie : D
Wykreślono to to samo co narysowano?
tak to ma wygladac?
zad 2....nielogiczne zupelnie : D
Wykreślono to to samo co narysowano?
tak to ma wygladac?
 Wiem, że
Wiem, że

 @pytajnik
2 α + β = 90, więc
90 − β = 2α
czyli ten kąt (ten zielony) wynosi 2α
skoro tak, a tamten jest trojkatem prostokatnym to ten trzeci kąt jest 90 − 2α czyli tak
wlasciwie β
więc
sin 2 α = x do jakiejś niewiadomej...oznaczylem ja jako y
stąd
x = y * sin 2α
@pytajnik
2 α + β = 90, więc
90 − β = 2α
czyli ten kąt (ten zielony) wynosi 2α
skoro tak, a tamten jest trojkatem prostokatnym to ten trzeci kąt jest 90 − 2α czyli tak
wlasciwie β
więc
sin 2 α = x do jakiejś niewiadomej...oznaczylem ja jako y
stąd
x = y * sin 2α
 ]
baju baj
]
baju baj


 ( S1 − środek pierwszego koła, S2− środek drugiego koła |S1S2| = r+R)
Troszkę podobne do tego zadania o które ja właśnie pytam tylko bez tej części o ciągach.
https://matematykaszkolna.pl/forum/310970.html
( S1 − środek pierwszego koła, S2− środek drugiego koła |S1S2| = r+R)
Troszkę podobne do tego zadania o które ja właśnie pytam tylko bez tej części o ciągach.
https://matematykaszkolna.pl/forum/310970.html
 Rozpatrujac nieskonczony ciag kol
Rozpatrujac nieskonczony ciag kol
 R − promień większego koła
r − mniejszego koła
x = r+R
y = R−r sin 30 = 1/2 = (R−r)/x
x = r+R
x = 2R − 2r
r+R = 2R −2r
R = 3r
c.n.u.
R − promień większego koła
r − mniejszego koła
x = r+R
y = R−r sin 30 = 1/2 = (R−r)/x
x = r+R
x = 2R − 2r
r+R = 2R −2r
R = 3r
c.n.u.
 Czytanie ze zrozumieniem: okrąg wpisany w wycinek koła o kącie środkowym 60o
2R= 2r+r+R ⇒ R=3r
Czytanie ze zrozumieniem: okrąg wpisany w wycinek koła o kącie środkowym 60o
2R= 2r+r+R ⇒ R=3r

 Rysunek trochę nie tak proporcjonalnie ale dane tak samo. Ten trójkąt jest podobny do tego z
kątem 30 stopni, więc ma też kąt 30 stopni.
Rysunek trochę nie tak proporcjonalnie ale dane tak samo. Ten trójkąt jest podobny do tego z
kątem 30 stopni, więc ma też kąt 30 stopni.






 Zobacz jeszcze do Antonow Sankin Zbior zadań z matematyki elelmentarnej
Tam tez jest dużo zadań z planimetrii .
jest tez ksiazka Waldemar Pompe W okol obrotow przewodnik po geometrii elementarnej
Kupilem ja za 12 zl (wydawnictwo szkolne Omega 2014r . Stron 48 ale wiedza kosztuje
Zobacz jeszcze do Antonow Sankin Zbior zadań z matematyki elelmentarnej
Tam tez jest dużo zadań z planimetrii .
jest tez ksiazka Waldemar Pompe W okol obrotow przewodnik po geometrii elementarnej
Kupilem ja za 12 zl (wydawnictwo szkolne Omega 2014r . Stron 48 ale wiedza kosztuje 



