szereg geometryczny i planimetria Archeolog: W kąt o mierze 60 stopni wpisano ciąg kół w taki sposób, że pierwsze kołó ma promień 8 i jest styczne do ramion kąta, a każde następne koło ma mniejszy promień i jest styczne do porzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu. A wiec w zbiorze pana Kiełbasy w odpowiedziach mamy wynik 81 pi, a po moich obliczeniach otrzymałem wynik 72 pi... Kto ma rację − Andrzej czy ja?

Jack: kazde nastepne jest mniejsze...ale o ile? czy to jest jakis szereg? (jak w nazwie − geometryczny ?)

Archeolog: To jest dokładne polecenie. O ile jest mniejsze trzeba już wyliczyć Nie chcę zbytnio pomagać, bo może mi to przeszkodzić w weryfikacji, czy moje obliczenia są dobre.

Archeolog: Ano jest szereg geometryczny (nieskończony ciąg geometryczny?), bo jak są wpisane w kąt, to promień rośnie o jakiś iloraz, a nie konkretną liczbę.

Jack: ciąg zbieżny....

	a1
czyli S =
	1−q

Archeolog: To jest prawie to samo co Eta ci podała nie licząc ciągu zbieżnego W sumie to co masz wykazać u Ety to jest promień wyrazu drugiego ciągu, jak to obliczysz to tamto też udowodnisz

Jack: ale to jest latwiejsze... r₂ + r₃ + ... + r_n = 4 do tego momentu narazie doszedlem

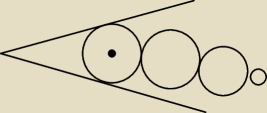
Jack: moglbys to narysowac...bo ja nie potrafie wyobrazic sobie ze jak mam ramie kata i pierwsze kolo jest najwieksze to kaade mniejsze dotyka ramion ktore sa coraz wieksze....w sensie : patrz rysunek... one by musialo sie chowac do tego kata...

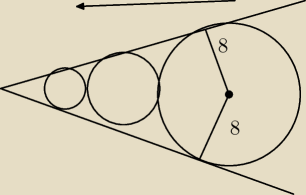
Jack: ja widze to w ten sposob

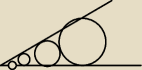
Archeolog: No widzisz i tutaj się pojawia magia. Jest napisane, że "Pierwsze koło", ale gdzie mamy "początek?"? Artystą to ja nie jestem, ale te największe koło jest "pierwsze" i kolejne są coraz mniejsze i styczne i spełniają wymagania... i tak w nieskończoność coraz mniejsze. U Ety jest to samo tylko tam jest jedno koło wpisane (duże) i jedno malutkie.

Archeolog: Dobrze narysowałeś.

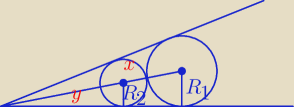
Godzio: Wychodzi, że Ty masz rację. R₁ = 8

	R1
sin30o =		⇒ x = 2R1
	x

	R2
sin30o =		⇒ y = 2R2
	y

	1
x = y + R2 + R1 ⇒ 2R1 = 3R2 + R1 ⇒ R2 =		R1
	3

	1
Otrzymujemy nieskończony ciąg geometryczny o ilorazie q =
	3

	1		1
R3 =		R2 =		R1 itd.
	3		9

Suma pól:

	1		1
P1 + P2 + ... = πR12 + πR22 + ... = πR12(1 +		+		+ ...) =
	9		92

	1		9
= π * 64 *		= π * 64 *		= 72π
	1   1 −   9		8

Jack: @Godzio...dokladnie

	1
q =
	3

ale dlaczego mówisz że R1 = 1 a nie 8 ?

Godzio: A gdzie tak napisałem?

Archeolog: Pierwszy wyraz Jack jest po prawej od jedynki.

Jack: a nie, przepraszam...wyjales R przed nawias...no tak P+P₂ + ... = πR₁² + πR₂² + ... = πR₁²(1+1/9...) Czyli to co napisales nom, to sie zgadza 72 pi

Archeolog: Muszę poprawić w odpowiedziach i ostrzec znajomego, bo już były nerwy z powodu błędnych odpowiedzi nie raz... No ale każdemu się może zdarzyć raz na jakiś czas gafę w matmie strzelić. Jeszcze robiłem takie http://www.zadania.info/8898720 zadanie i udowodniłem inaczej − dzięki dwóm kątom opartym na średnicach okręgu. Zaliczyliby na maturze czy musiałbym koniecznie ten trapez zauważyć?

utem:

	R
sin30o=
	|OB|

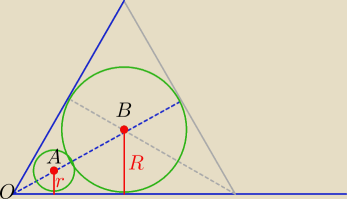
|OB|=2*8=16 |OA|=2r |OB|=|OA|+r+8 16=3r+8 3r=8

	8
r=
	3

S₁=π*8²=64π

	8		64
S2=π*(		)2=		π
	3		9

	649π		1
q=		=
	64π		9

	1		9
S=64π*		=64π*		=72π
	1   1−   9		8

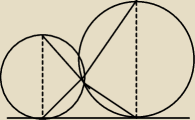
Archeolog: Przepraszam za krzywiznę, ale mam nadzieję, że widać o co chodzi.

Godzio: A gdzie są te kąty oparte na średnicach?

Godzio: A kto powiedział, że przedłużenie przetnie się w tamtym punkcie? To też trzeba uzasadnić.

Archeolog: Jeśli okręgi są styczne do prostej to prosta prostopadła do okręgu przejdzie przez średnicę i będzie równa 2r. Później jest tam jakieś twierdzenie o tych kątach na średnicach które pokazuje nam, że tworzą się 2 kąty 90 stopni które mają wspólny punkt P i są przez to kątami odpowiadającymi. I jak mamy kąty odpowiadające 90 stopni to nie ma innej opcji niż żeby kąty między nimi dopełniające do 360 nie były odpowiadające i nie miały kolejno po 90 stopni. Oczywiście jakoś ładniej bym to ujął na maturce(słownictw) i wykorzystał zmienne których nie umiem dodawać na tej stronie do rysunków... Przeszło by?

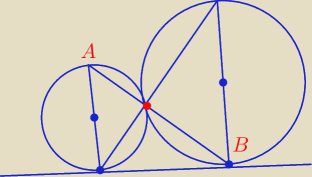
Godzio: Nie widzę uzasadnienia, że prosta AB przechodzi przez punkt styczności okręgów. To co piszesz to prawda, ale wciąż to za mało.

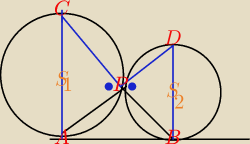
Archeolog: Dołączam rysunek.

Archeolog: To ja już nie wiem co jeszcze mógłbym dodać żeby to było prawdziwe...

Godzio: Wszystko to co napisałeś jest poprawne, ale dlaczego odcinki (z Twojego rysunku) AD i BC przecinają się w punkcie styczności, a nie gdzie indziej?

Archeolog: Bo mamy już odcinki AP i PB które spotykają się w jednym miejscu i te odcinki są t ylko dopełnieniem żeby zagwarantować kąt 90 stopni, więc muszą być ustawione pod kątem prostym.

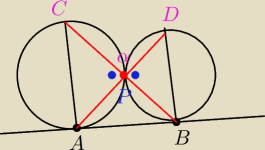
Jack: A nie wystarczy , że w trójkącie opartym na średnicy kąt wpisany ma miarę 90 stopni. kąt |∡APB| + α = 360 − 180 = 180 Kąty wierzchołkowe są tej samej miary, czyli zarówno α jak i kąt |∡APB| mają po 90 stopni...

Godzio: Archeolog nie masz racji, AP i PB się przecinają, ale skąd wiesz, że ich przedłużenia trafią w drugi koniec średnicy?

Archeolog: Godzio ja już nie wiem, poddaje się. To że są przedłużeniami wyszło mi z tego kątu 90stopni, ja ich 'na siłę' nie przedłużałem nie bij proszę To raczej narysowanie średnicy i od niej odcinka do punktu P sprawiło że mam 100% szans na kąt 90 stopni, a że one są styczne to takie same kąty będę miały i co za tym idzie jak są kąty wierzchołkowe to te proste "łączą" się kątem 180 stopni czyli są przedłużeniami.

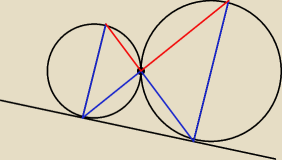
Godzio: Niebieski odcinki masz dane, skąd wiesz, że czerwone odcinki wraz z niebieskimi tworzą linie prostą? O to mi się rozchodzi

Archeolog: Ja już mam tak namieszane w głowie że nie ma szans żebym się z tego wytłumaczył. Planimetria i ogółem figury to coś przez co się raczej nie dostanę na studia xP albo przez infe.

Godzio: Zaraz Ci to pokażę.

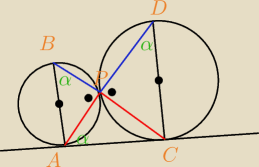
Godzio: Skorzystamy z cechy (k,k,k). Kąty APB i CPD są równe 90^o jako kąty oparte na średnicy. Oznaczmy kąt PAC = α, kąt APC jest dopełnieniem kąta 90^o więc też równy 90^o. Kąt ACP = 180^o − 90^o − α = 90^o − α. Kąt między promieniem, a styczną jest równy 90^o więc BAP = 90^o − α ⇒ ABP = α oraz DCP = 90^o − (90^o − α) = α ⇒ CDP = 90^o − α Mamy równość trzech kątów ⇒ trójkąty są podobne, zatem punkty A,P,D oraz C,P,B są współliniowe

Archeolog: Czekam z niecierpliwością, bo mój mózg strajkuje że kolejnego zadania nie liczy póki nie zobaczy o co ci tu chodziło.

Archeolog: Godzio, ale to trzeba by w zadaniu udowadniać? Bo teoretycznie to, że kąt APC jest 90 stopni mamy w drugiej linijce.

Godzio: Tak, bo ciągle wchodzi to samo, Ty nie wiesz czy PD to odcinek łączący koniec średnicy z punktem styczności.

Godzio: Narysuje Ci antyprzykład.

Archeolog: Ale jak podają we wzorach "Kąt oparty na średnicy jest kątem prostym", a ja sobie sam założyłem rysując go że on łączy punkt na końcu średnicy z tym punktem P?

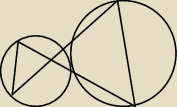
Godzio: Oczywiście wiadomo, że to bezsensowny rysunek bo my wiemy, że proste są równoległe, ale chodzi o pokazanie idei tego co pokazywałem. Punkt przecięcia ma leżeć w punkcie styczności. Wtedy można korzystać ze wszystkich faktów. Ja w dowodzie łączę końce średnic z punktem styczności, ale nie wiem, że te kąty oparte na średnicy są wierzchołkowe.

Archeolog: To jakby dodać że te średnice są równoległe do siebie i tworzą te kąty w jednym punkcie to by było wszystko ok? A poprzeć ten fakt tym, że wychodzą z punktów A i B i są prostopadłe do tej samej prostej.

Godzio: Moim zdaniem trzeba uzasadnić to tym co napisałem w poście o 23:41

Archeolog: Ok, dopiszę do mojego dowodu w zeszyciku i teraz na pewno będę o tym konkretnym zadaniu i podobnym pamiętał xP Dzięki za wszystko Godzio i dzięki innym za upewnienie mnie w wyniku tamtego poprzedniego zadania!

5-latek: Widzialem ze robisz tez zadania dr Pompe . tez mam je gdzies zapisane . Kup sobie jego ksiazke kosztuje około 12 zl pt. W okół obrotow

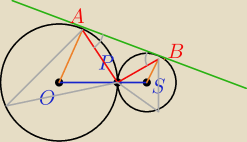
Kacper: |∡AOS|+|∡BSO|=180^o ⇒ suma miar "szarych" kątów jest równa 90^o ⇒ |∡PAB|+|∡PBA|=90^o c.k.w