Geometria dowod Marcin: W trójkącie prostokątnym ABC w którym bok AB to przeciw prostokątna, na boku BC wybrano punkt d taki, ze kąt DAB = 2 razy kąt CAD. Długość BD to a, a kąt CAD ma miarę alfa. Udowodnij, że AD = a(1−4sin2 alfa/2sin alfa

Eta:

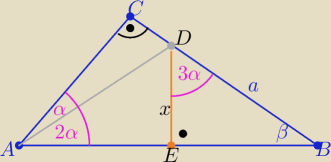
	x
W ΔEBD : cos(3α)=		⇒ x= a*cos(3α)
	a

	x		x		acos(3α)
W ΔAED : sin(2α)=		⇒ |AD|=		=
	|AD|		sin(2α)		sin(2α)

	acosα(4cos2α−3)		a(4(1−sin2α)−3		a(1−4sin2α)
|AD|=		=		=
	2sinα*cosα		2sinα		2sinα

c.n.u Wykorzystując wzory : cos(3α)= cosα(4cos²α−3) i sin(2α)= 2sinα*cosα

Ania: mogę mieć pytanie? skąd wiemy, że kąt BDE to 3 alfa?

Kacper: Liczysz kąty

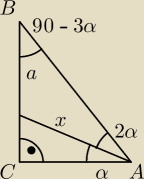
Kacper: Lub tak

a		x		acos(3α)
	=		⇒ x=
sin2α		sin(90−3α)		sin2α

piotr1973: cos(3α) = cos(α) (−1+2 cos(2α))

6latek: